Definitions

Elements of base

1) Set :

Collection (class, family) of said objects elements of together.

 

2) Sottoset :

To it is sottoset of B if B contains all the elements of To but it does not contain all the elements of B.

 

3) Sottoset appropriate :

A sottoset it is just if it is a sottoset not empty.

 

4) Brace ordinata:

Draft of one brace constituted from an element of with C$r-at and from an element of the B entirety in the order.

 

5) produced Entirety cartesian To x B:

Are the entirety formed from all the tidy braces con to?A e b?B.

 

6) Relationship :

It is preached binary (an affirmation that it can be true or false) r(x, y) with x?X and y?Y

 

7) Property of riflessività:

to £ to

 

8) Property of symmetry :

" x, y ? X se x " y ž y " x

9) Property of asymmetry :

" x, y ? X se x £ y ^ y £ x then y = x

10) Property of transitività:

" x, y, z ? X se x £ y ^ y £ z allora x £ z

11) Ordering total :

Total is had an ordering if taken however to 2 elements x and y they are confrontabili ossia x £ y oppure y £ x.

 

12) Maggiorante:

An element k ? X maggiorante of To if is said

a) " to?To it is had that k he is confrontabile with to

b) " to?To it is had that to £ k

 

13) Minorante:

An element k ? X minorante of To if is said

a) " to?To it is had that k he is confrontabile with to

b) " to?To it is had that to ³ k

 

14) Maximum :

It is a maggiorante that belongs to with To

 

15) Minimum :

It is a minorante that belongs to with To

 

16) Sup A said extreme superiore:

It is smallest of the maggioranti of To.

 

17) Inf A said extreme inferiore:

He is largest of the minoranti of To.

Functions

18) Function :

It is a correspondence univoca from X in Y that is associates to every element ? X a single element ? Y

 

19) Succession :

Is one function having like dominion ?

 

20) Function iniettiva:

It is a function for which to a single element of the image a single element of the dominion corresponds.

 

21) Function suriettiva:

Is one function having like image all the codominio.

 

22) Function biiettiva:

It is a function that is is iniettiva that suriettiva.

 

23) Entirety numerabile:

It is an entirety that can be put in correspondence biunivoca with ?.

 

24) Function rising :

A relationship is a having function increases them ³ 0

 

25) Function derising :

A relationship is a having function increases them £ 0

 

26) Function pari:

It is a function for which f(x) = f(-x)

 

27) Function dispari:

It is a function for which f(-x) = - f(x)

 

28) g°f:

It means to apply the function g to the function f (x)

 

29) Inequality triangular :

|x₁ x₂| £ |x₁| |x₂|

 

30) Inequality of Young:

2|xy| £ and x² y²/ and

31) Inequality of Cauchy - Schwarz:

2|xy| £ x² y²

Vectorial space "ⁿ

32) Product scalar : " x, y ? "ⁿ ,

33) Norm euclidea : " x ? "ⁿ ,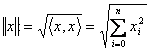

34) Euclidean Distance: " x, y ? "ⁿ ,

 

35) a function defined on a real vectorial space X comes defined norm if it enjoys following the 3 property:

a) " x ? X, ||x|| ³ 0 e ||x|| = 0 > x = 0

b) " x?X, " y?" ||lx|| = |l|*||x||

c) " x, y ?X ||x y|| £ ||x|| ||y||

 

36) a function defined on one with X comes defined distance if it enjoys following the 3 property:

to) " x, y ? X, d(x, y) ³ 0 and d(x, y) = 0 > x = y

b) " x,y?X, d(x, y) = d(y, x)

c) " x, y, z ?X d(x, y) £ d(x, z) d(z, y)

37) discreet Distance:

if x = y ž d^~ (x,y) = 0

if x ¹ y ž d^~ (x,y) = 1

38) d*(x, y):

max{|x₁ - y₁| , |x₂ - y₂|}

39) d_*(x,y):

|x₁ - y₁| |x₂ - y₂|

Topology

40) Around :

Data x ? "ⁿ and and ?" , is said around spherical of center x and beam and the entirety B_and(x): = { y? "ⁿ : d(x, y) < and}

41) Sphere :

Data x ? "ⁿ and and ?" , says sphere of center x and beam and the entirety S_and(x): = { y? "ⁿ : d(x, y) = and}

42) Are X an entirety, for every x?X one is had family of intorni with the following property:

to) x ? Every U(x) for x ? X.

b) If U₁(x) and ₂U(x) are 2 intorni of x ž their intersection contain at least one around of x.

c) if y?U(x) ž around exists a contained U(y) of y in U(x)

d) if x ¹ y ž exists a disgiunti U(x) of x around and one around U(y) of y: U(x) ? U(y) = 0

 

43) R^{* :}

Extensive R saying is R^* : = " ? {-¥} ? { ¥}

44) R ^:

R saying point is R^. : = " ? {¥}

45) inner Point:

One point x ? "ⁿ inside to together is said and if its completely contained exists around in and

46) Describe the set

It is the entirety constituted from the single inner points of and.

 

47) external Point:

One point x ? "ⁿ outside to together is said and if it is inner to the complementary one of and.

48) Point of frontier:

One point x ? "ⁿ one says of frontier if it is not inner of external to and.

49) Describe set the ¶and:

It is the entirety constituted from the single points of frontier of and.

 

50) Point of accumulation:

One point x ? "ⁿ one says of accumulation for and if every around of x it contains one point of and various from x.

51) Describe set the E':

It is the entirety constituted from the single points of accumulation of and.

 

52) isolated Point:

One point x ? "ⁿ is said isolated point of and if x?And and it is not of accumulation for and.

53) With opened:

Together and  "ⁿ it is said opened in "ⁿ if every element of and is stung inner to and.

54) closed Entirety:

Together and  "ⁿ it is said closed in "ⁿ if the complementary one is with open.

55) With limited:

Together and  "ⁿ one says limited in "ⁿ if a r exists such that and is contained in around of the beam origin r.

56) Diameter of a Diam(E) entirety:

Diameter is defined of with the advanced end of with of the distances between 2 pertaining points x and y to and.

 

57) Closing of and that is :

It is the entirety formed from the union of and with its frontier.

 

58) With convex:

An entirety says and  "ⁿ the combining segment is said convex if for every brace (x,y) the 2 points is contained in and.

Limits

59) limited Function:

A function is said limited in To  X if such one exists one M that ||f(x)|| £ M " x?To.

 

60) total or absolute Maximum:

M ? " is said total or absolute maximum of f in To if x exist₀ ? To such that:

to) f(x) every £ M for x ? To

b) f(x₀) = M

 

61) total or absolute Minimum:

m ? " is said total or absolute minimum of f in To if x exist₀ ? To such that:

to) f(x) every ³ m for x ? To

b) f(x₀) = m

 

62) Point of local minimum and minimal premises:

One point x₀ says of local minimum if a such U(x ₀ existsaround) that f(x) ³ f(x₀) for every x pertaining to around.

The point is of local minimum if f(x) > f(x ₀)for strongly every x pertaining to around to exclusion of x₀ .

 

63) Point of local maximum and maximum premises:

One point x₀ says of local maximum if a such U(x ₀ existsaround) that f(x) £ f(x₀) for every x pertaining to around.

The point is of local maximum if f(x) < f(x ₀)for strongly every x pertaining to around to exclusion of x₀ .

 

64) Limit:

If x₀ ? "^* it is a point of accumulation for X ž l ? "^* is said limit of f(x) for x ® x₀ if for every around V of l one U of x ₀ suchexists around that for every element x pertaining to this around to exclusion of x₀ is had that f(x) ? V.

If then x₀? " and l?" can equivalent be written: "and> 0, $d> 0 such that " x?X, 0 < |x-x₀| < d it is had that |f(x) - l | < and

 

65) Around skillful:

It is interval [ x₀ , x₀ and)

 

66) Point of skillful accumulation:

A skillful point of accumulation is had when in every around skillful of this point there is at least an other point of together.

 

67) skillful Limit:

If x₀ ? "^* it is a skillful point of accumulation for X ž l ? "^* is said skillful limit of f(x) for x ® x₀ if for every around V of l one skillful U ofx ₀ suchexists around that for every element x pertaining to this around to exclusion of x₀ is had that f(x) ? V.

 

68) Point of end:

It is a minimum or maximum point.

 

69) Definition of limit of one succession:

> " and> 0 exist a N?? such that for every n > N is had that |to_n - l |<and

 

70) Rules of or piccolo:

to) o(3x) = o(x)

b) o(x) o(x²) = o(x²) for x® ¥ while it is one o(x) for x®0

c) x² * o(x) = o(x³)

d) o(o(x)) = o(x)

 

71) When f(x) = O(g(x))?

When it is f(x) that g(x) they are 2 infinite or infinitesimal functions but their relationship has an ended limit.

 

72) When f(x) ~ g(x)?

When it is f(x) that g(x) they are 2 infinite or infinitesimal functions for x ® x₀ but their relationship is unitary.

 

73) Conditions for the oblique asymptote:

to) a limit ended To for x ¥of®relationship f(x)/x must be had, analogous for x® -¥.

b) If the ended limit is found then the asymptote exists if the limit for x® ¥ of f(x) - Ax gives back ended a B value that corresponds to the former to the origin of the asymptote. In such case the asymptote has equation y = Ax B.

 

74) Conditions for the vertical asymptote:

The vertical asymptote is had when the limit for x®x₀ of the function is ±¥ is from right that they give on one side left or single.

 

75) Definition of subsuccession :

A succession {b_n} says subsuccession of the succession {to_n} if closely increasing succession {k _n}withvalues in exists one? such that b_n = to_Kn every for n??.

 

76) Definition of fundamental succession:

A succession {to_n} to real values says fundamental or of Cauchy if "and> 0 exist a N?? such that |to_n- to_m| <and for every brace n, m > N.

77) Definition of with compact for successions:

A K entirety says compact for successions if every succession to values in convergent K has one subsuccession to an element of K.

Continuity

78) Definition of continuity:

A function is said continues in x₀ ?X if one of following is verified:

to) x₀ are one isolated point of X.

b) x₀ are one point of accumulation for X and .

It is equivalent to the definition of limit but with the warning to consider also point x₀ that instead for the limits is ignored.

 

79) Definition of dismissable discontinuity in x₀ :

Is had one dismissable discontinuity in x₀ ? to the dominion if it exists ended the limit for x®x₀ but is various from f(x₀).

 

80) Definition of discontinuity of 1ª species (or jump) in x₀ :

Is had one discontinuity of 1ª species in x₀ ? to the dominion if they exist ended the limits for x®x₀ is from right that they give left but they are between various they.

 

81) Definition of discontinuity of 2ª species in x₀ :

Is had one discontinuity of 2ª species in x₀ ? to the dominion in the case in which at least one of the 2 limits it does not exist or it is infinite.

 

82) Definition of function uniform continues:

The function f says uniform continues if for every and> 0 a d exists > 0 such that for every brace x,y ?X with ||x-y||<d it is had that || f(x) - f(y) || <and .

 

83) Definition of lipschitziana function:

The function f says lipschitziana in X if constant L such ³ 0 exists one that || f(x) - f(y) || £ L ||x-y|| for every x,y ? X.

 

84) Definition of Holderiana function:

The function f says lipschitziana in X if they exist of the constants L > 0 and 0<to< 1 such that || f(x) - f(y) || £ L ||x-y||^to for every x,y ? X. Where to order of Holderianità is said.

85) Definition of oscillation of one function:

The oscillation of a function w in To can assume the following values:

¥ if f it is not limited in To

sup f - inf f if f it is limited in To

Derivabilità

86) Equation of the straight tangent to the diagram of the function in point (x₀ , f(x₀)):

y = f(x₀) m(x-x₀)

 

87) Definition of derivabile function:

A function says derivabile if it exists ended limite the if such limit exists comes called derived.

 

88) Definition of skillful derivative:

If it exists ended limite the it comes called derived skillful.

 

89) Definition of angular point:

An angular point is had if f it is continuous in x₀ and the limit of the derivative from right is various from the limit of the derivative from left, is noticed that one of the 2 can also be infinite.

 

90) cuspid Definition:

A cuspid is had when the derivative before from right and the derivative before from left are infinites of opposite sign.

 

91) Definition of primitiva function:

A F function says primitiva of f in if:

a) f is derivabile in I

b) every F' (x) = f(x) for x ? I

In good substance one primitiva is the function that I have before deriving and in order to recover I have it the necessity to integrate.

 

92) Definition of convex function:

A function f is said convex in an interval if for every brace x,y?The segment of ends (x, f(x)) (y, f(y)) does not have points under the diagram of f.

In other words it can be written that f it is convex in the > for every x,y?I, x¹y and for every t ? (0.1) is had:

f((1-t)x ty) £ (1-t)f(x) tf(y).

93) Definition of point of flexed :

A point of flexed is had if a skillful one of x exists around₀ in which the function it is concave and around left in which the function it is convex or viceversa.

More variable functions

94-a) Definition of limit in "ⁿ by means of the cartesian coordinates:

if for every around V of l one U of x exists around₀ in "^{. n} such that for every x pertaining to this around with the exception of x₀ is had that f(x)?V.

 

94-b) Definition of limit in "ⁿ by means of the polar coordinates:

" uniform regarding q

that is " around V of l such $ d > 0 that " 0 < r < d and "q ha

95) Definition of directional derivative:

If v are one payer pertaining to "ⁿ and the function j_v (t) = f(x tv) is derivabile in t=0 then is defined derived directional in direction v of f in x the limit.

 

96) Definition of partial derivative:

It is defined derived partial ognuna of the directional derivatives carried out in the direction of one of the carriers of the canonical base of the vectorial space accommodating.

 

97) When a function says derivabile in a point:

When in that point the partial derivatives exist all and therefore the gradient exists.

 

98) Definition of function having like differentiable dominion "in a point:

A function f is differentiable in one point x?(a,b) if ah o(h) for h 0 exist to a such one that f(x h)=®f(x).

 

99) Definition of differentiates them:

It differentiates them df(x) represents the increment endured from the function as a result of an increment in the dominion and therefore coincides with the product df(x) = f â(x)dx where dx = x-x₀ .

 

100) Definition of function having like dominion "ⁿdifferentiable in a point:

A function f is differentiable in one point x?(a,b) if it exists to? "ⁿ such that f(x h) = f(x) < a,h > o(||h||) for h®0.

101) Meant of the affirmation f?C¹(x)?

It means that f he is derivabile in X? "ⁿ and all the partial derivatives are continuous in X.

 

102) What is differentiates them second and as it is indicated?

d²f(x) = < H_f (x)dx, dx >

 

103) Write the expression of differentiates them of order k in x:

 

104) Polynomial di Taylor:

If f he is m times differentiable in x?X the function is said polynomial of Taylor of degree m of f around to x:

 

105) Definition of convex function:

A function is said convex in To with open and convex if for every brace x,y f((1-t)x ty) comprised £ tf(x) (1-t)f(y) for every t between 0 and 1.

 

106) critical Point:

One point x?To with opened critical point of f is said if f he is differentiable in x and if `f(x) = 0 for every payer v? "ⁿ .

 

107) saddleback Point:

One point x₀ says of saddleback for f if x₀ are one critical point of f and if function f(x) - f(x₀) admits positive values you and values denied to you in whichever around of x₀ .

Integrals

108) Subdivision:

A subdivision of the interval [ a,b ] is an ended entirety of points comprised between to and b

 

109) When a subdivision is finer than an other:

A subdivision is finer than an other if it contains at least a point in more.

 

110) inferior Sum s(D, f):

Inferior sum to the D subdivision is said relative the amount that is the sum of the areas of the rectangles everyone of which has like base an interval of the subdivision and like height, the minimum assumed from the function in that spaces out.

 

111) advanced Sum S(D, f):

Advanced sum to the D subdivision is said relative the amount that is the sum of the areas of the rectangles everyone of which has like base an interval of the subdivision and like height, the maximum assumed from the function in that spaces out.

 

112) integrable Function second Riemann:

A limited function says integrable according to Riemann in the interval [ a,b ] if it turns out that that is if the advanced end of with of the inferior sums is equal to the inferior end of with of the advanced sums.

 

113) Amplitude of the subdivision |D| :

The length of largest is said amplitude of the subdivision of the intervallini characterizes to you from the subdivision.

 

114) integral Sums (to the Riemann):

Being m the value of the limit in an inner point to the interval is had that and if a function is integrable according to Riemann ž for every and > 0 D subdivision exists onesuch _and that | I(f) - s(D_and , f) | < and .

115) If f integrable function in [ is one a,b ] and c?[ a,b ] then very the integral function of f relative is defined to point c

every for x?[ a,b ]

 

116) integrable Function in improper sense:

The 2 following cases are introduced:

to) One function f: (a,b ]® " with to?"ã?{-¥} that he is integrable according to Riemann " w?(a,b) integrable in is said improper sense if it exists ended the limit

b) One function f: [ a,b)® " with b?"ã?{ ¥} that he is integrable according to Riemann " w?(a,b) integrable in is said improper sense if it exists ended the limit .

117) absolutely integrable Function in improper sense:

A defined function f on an interval is absolutely integrable in improper sense if | f | he is integrable in improper sense on the interval stesso.