1) Maggiorante:

Given one with ordered X and one its sottoset naturally ordered To, then a maggiorante of To is whichever element of X that is confrontabile con " element to of To and it follows it or it is to equal it.

2) With limited advancedly:

A maggiorante is an at least having entirety.

3) advanced End:

Given one with ordered X and one its sottoset naturally ordered To, then a maggiorante of To is whichever element of X that is confrontabile con " element to of To and it follows it or it is to equal it. Smallest than these maggioranti advanced end of To is called or Sup To advanced extreme Tale is only.

4) Maximum:

If the comprised maggiorante of with To in X beyond belonging to X belongs also to then such element defines Maximum and it is indicated with Max To maximum Tale is only.

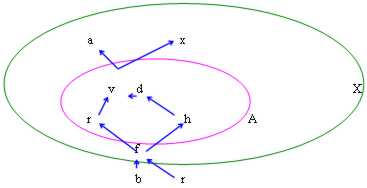
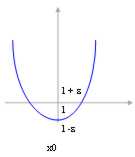
In this figure we have the following cases:

maggioranti : v, to, x exists therefore To is limited advancedly

minoranti : f, b, x exists therefore To is limited inferiorly

Sup A : the smallest of the maggioranti is v

Inf A : the largest of the minoranti is f

Max A : is always v in how much beyond to being smallest of the maggioranti also is comprised in To

Min A : is always f in how much beyond to being largest of the minoranti also is comprised in To

5) Minorante:

Given one with ordered X and one its sottoset naturally ordered To, then a minorante of To is whichever element of X that is confrontabile con " element to of To and it precedes it.

6) With limited inferiorly:

A minorante is an at least having entirety.

7) inferior End:

Given one with ordered X and one its sottoset naturally ordered To, then a minorante of To is whichever element of X that is confrontabile con " element to of To and it precedes it. Largest than these minoranti inferior end of To is called or Inf To inferior extreme Tale is only.

8) Minimum:

If the comprised minorante della with To in X beyond belonging to X belongs also to then such element defines Minimum and it is indicated with min To minimal Tale is only.

9) ended Entirety:

With To one says ended if it has a n° ended of elements that is exists a n ? ? such that the n° of elements of To is n.

If with ordered To it is ended and not empty then it admits minimum and maximum.

10) Sets numerical:

Sets X that is to one brace of numbers in X is constituted from elements calls® to you ânumeriâ? pertaining to with X x X is associated a solo n° in X that is function of the indicated operation.

The always possible operations in with numerical are following:

Addition between following numbers with the 4 property or axioms:

a) ASSOCIATIVE ž " x, y, z x y z = (x y) z = x (y z)

b) COMMUTATIVA ž " x, y x y = y x

c) ZERO ž " x ? x 0 = x

d) NUMBER OPPOSTO ž " x $ - x : x - x = 0

Multiplication between following numbers with the 4 property or axioms:

a) ASSOCIATIVE ž " x, y, z x (yz) = (xy)z = (xz)y

b) UNITA' ž " x x * 1 = x

c) COMMUTATIVA ž " x, y xy = yx

d) RECIPROCO ž " x ¹ 0 $! n°: x * x^-1 = 1

Moreover somma and multiplication is tied from the following distributive property:

a) DISTRIBUTIVE SOMMA ž " x, y, z x (y z) = (xy) (xz)

Moreover following are defined:

Property of density or of you add a place to table

Given to 2 elements whichever x and y, between of they exist infinites elements of Q, than they can be gained making the arithmetic mean between x and y, operation that in Q is concurred.

Property of Archimede or of the jump

Given to 2 elements whichever x and y, di Q, with x < y then exist always a n° n that, multiplied for x, it gives the relation to me

nx > y

in fact enough to consider the n like fractions and to place n equal to the product between the denominator of x and the numerator of y.

11) Representation decimates them:

It is a representation that sees the numbers rations expressed them not like fractions but like sets of n that they are ollowed and the same representatives they one weighed fraction but. Tasks to p , it is worth in notation decimates them

3.141592654 = the numbers decimates them in this case is illimita and gives life to you to a n° real to difference of the fractions between n first that gives life to alignments decimates limits them to you or periodic with period ¹ 9 in how much if the period is 9 it falls in a controsenso developing the formulas of the succession.

An alignment is defined JUST decimates them that it does not have 9 like periodo.

In Q the alignments decimali answer to following:

if x > 0 like as an example p :

3.141592654 < = x < 3,141592654

that is x are comprised between its value and its value more one anticchia, expressed gives

if x < 0 like to esempio - p :

- 3.141592654 - < x < = -3.141592654

that is x are comprised between its value less one anticchia, expressed from and the searched value, that for via of the incompletezza of with numerical Q.

12) Property of thoroughness of ":

If with To ? " ,e therefore tidy, it is limited superiormente(inferiormente) that is admits a maggiorante(minorante) at least, then it admits also extreme superiore(inferiore) that is exists a maggiorante(minorante) that precede(segue) the others

This in other words says to us that, a real number is not other that a section between two sets and represents the advanced end of the minor and the inferior end of the greater one of the 2 sets .

Dim ž two cases are introduced:

1) To is ended, exists the maximum (is also extreme advanced) of To being totally ordered.

2) To is infinite and then we must demonstrate that of all the maggioranti of To ce n' are one that is smaller of the others,

We proceed for steps succeeded to you that is;

* we take a maggiorante y₀ of To and an element to₀ of To.

* we characterize the intermediate point between the two elements that therefore divide to the interval in 2 others intervals.

* we choose the containing interval points of To and if they have them both, we choose that one of left.

* we characterize the intermediate point between the two elements that therefore the interval in 2 divides.

* we continue therefore finche the interval between an element of To and its maggioranti do not become small, tanto from ridursi to a single element that we will call y , or Sup To, this is gained from the fact that the series is not

decreasing has advanced limit in to_and and stretches to y .

the length of the last interval is worth (y₀ - to₀)/2ⁿ.

Obtained intervals therefore are like contained Russian dolls one in the other.

y_n > = a, " to ? To and " n that is the value of the last found maggiorante he is still advanced to to

we must hour to demonstrate that this number is really the Sup To that is that answers to the 2 following:

to) " to ? To, < = y

This is demonstrated for absurdity saying that an element to ofTo that exists is greater of y then if we take the distance to - y and we call it d_{a - y} we can take a n such to characterize an interval (y₀ - to₀)/2ⁿ < d_{a - y} we will gain that:

con nsuch = n to characterize a maggiorante smaller than y

y = SupA characterized from the divisions

y_n = associated Y to n

this formula us door to a controsenso in how much y_n is smaller of y that therefore is the true Sup To.

b) " and < 0 $ to ? To: to > y - and

That is hardly we go away a Pò from y before what that we meet is an element to of To.

Also this demonstrates for absurdity placing that " element ? To, it is smaller of y - and.

this would mean that between y - and , and y_n not is elements of To but if we choose n^a that is smaller than and then in the interval that it delimits not will be some point of To, and this is discorde with what it had been our criterion of search, therefore is an absurdity.

Demonstrated how much for the advanced end is worth also for the inferior end.

N.B. The previous demonstration is draft from Mathematical Analysis 1 and is apparently various from that we find on the Lessons of A.m.1 in how much that one has an approach legacy to the numbers decimates them illimita to you.

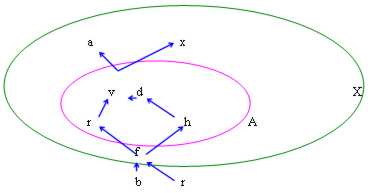
In , v and f always exist if it considers you like Sup To and Inf To, not like Max To or Min To.

13) Theorem of Bolzano - Weierstrass:

We have together and ? "ⁿ with characteristic following:

* limited (exists a r > 0 such that and is contained in around of center Or and beam r)

* infinito (with To says infinite if it has a n° infinitely of elements that is does not exist a n ? ? such that n° of the elements of To is n).

Then in "ⁿ point exists at least an accumulation point (in whose around there are infinites heads of and) of and.

Demonstration:

1) We must find a candidate to being stung of accumulation

cos¬ as we have made in order to analogous demonstrate the thoroughness of " us muoviamo for "² , stavolta but instead considering intervals on a straight one we will consider areas and in particular areas of rectangles. We have supposed To limited purposely to the aim of being able to enclose it in a circle but we know well that enclosing it in a rectangle it does not change null of determining.

Chiameremo T₀ this containing rectangle ours infinite entirety and.

* we subdivide T₀ with projections to, b, c, d in 4 equal parts creating therefore others 4 rectangles

* We call T_{the 1} rectangle that second we contains ¥ heads of and (ce n' it is sure 1 inasmuch as and it is un infinite entirety).

* We subdivide T₁ in analogous way and reproduce the algorithm until characterizing a sufficiently small rectangle and that it still contains infinites heads of and.

* we have therefore the following relations:

1) the side sx of a whichever constructed rectangle therefore cannot that have abscissa > or = to the side sx of the rectangle that precedes it and < or = to the side sx of the rectangle of which it is origin.

2) the side dx of a whichever constructed rectangle therefore cannot that have abscissa < or = to the side dx of the rectangle that precedes it and > or = to the side dx of the rectangle of which it is origin.

1°2) Whichever rectangle obtained in the series will have the abscissa of the side sx < of the abscissa of the side dx of whichever other rectangle of the series.

3) the side low of a whichever constructed rectangle therefore cannot that have ordinata > or = to the side low of the rectangle that precedes it and < or = to the side low of the rectangle of which it is origin.

4) the high of a whichever rectangle therefore constructed side cannot that have tidy < or = to the side dx of the rectangle that precedes it and > or = to the high side of the rectangle of which it is origin.

3°4) Whichever rectangle obtained in the series will have the former of the side basso < of the former of the high side of whichever other rectangle of the series.

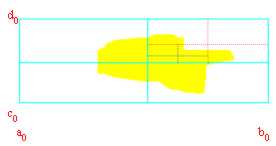
And therefore defining:

To = with of the abscissas of the Dx sides of the series of the rectangles.

B = with of the abscissas of the Sx sides of the series of the rectangles.

C = with of the formers of low sides of the series of the rectangles.

D = with of the formers of low sides of the series of the rectangles.

* we can say that whichever element of B is maggiorante of a whichever element of To

* we can say that whichever element of To is minorante of a whichever element of B

therefore for the thoroughness property, the Sup exists To and the Min B and in the fattispecie we can also assert that the Sup To < = Inf B and in order to render the 2 values equal we must make that the distance becomes 0 that it is obtained low working on the side of the last one rettangolino that is worth amount that stretches to zero to growing of n, that is of the n° of rettangolini uses you. Therefore we can choose n such to obtain Sup A = Inf B.

Analogous we behave ourselves on sets the C and D until determining the Sup of C = Inf D.

Therefore our candidate is the point x(Sup To, Inf D).

2) We must hour to demonstrate that this point is really an accumulation point.

Must that is be demonstrated that in around of center x and beam and are infinites head of and, but this will happen sure if of those rettangolini that we have used ve of it is one that is contained completely in around of our point of accumulation, this why everyone of those rettangolini had been constructed with the criterion that contained infinites heads of and.

But for being sure that the rettangolino it falls in around we must make yes that its diagonal (diam T_n ) is inferior to the beam of around

if the diagonal of T₀ , diam T₀ = then diam T_n =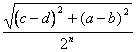

we must that is place but this is a n° that sure the Theorem of Archimedes exists in fact says to us that enough to multiply r for a n° opportune.

In particular a square in the circle can be registered and to demonstrate that the rettangolino it is contained therefore a square possesses infinites heads of and and therefore also around of our point x that can therefore be defined to full load tito it like point of accumulation of together and limited and infinitely.

14) Topology in "ⁿ

Topology is defined that branch of the mathematics that is taken care of the study of the smallest entity, imprecisa, but of great usefullness, around.

15) Around spherical:

It is x ? "ⁿ and r ? ",

it is defined as making part of around the spherical one of center x and beam r every point whose distance from x is inferior to " distinguish the following cases:

n = 1 ž around delimits the interval (x-r, x r)con the excluded ends.

n = 2 ž around delimits of the circles concentrates us of inferior beam to r

n = 3 ž around delimits of the full spheres centered in x and of beam r lacking in the edge.

16) Sphere:

Is defined instead sphere of center x ? "ⁿ and beam r ? ", all the points whose distance from x is exactly r.

n = 1 ž the sphere characterizes single the 2 points (x-r, x r).

n = 2 ž the sphere characterizes the single external circumference, is excluded all the inner points.

n = 3 ž the sphere only delimits the edge of the spheres with center x and beam r.

Naturally it can be thought to " as to an entirety constituted of infinites it aims everyone of which is equipped of a just around U_(x) or, in order better to say, than one having family of intorni the following property:

1) x ? U(x) that is x belongs around to its

2) if to one same x, correspond 2 intorni, then the intersection of these 2 intorni is still one around of x

3) if a point y ? to around of x then one around of y exist completely contained in around of x

4) if 2 points are separates to you, (as as an example in Q) then is separates also theirs to you intorni.

If in an entirety these are respected all proprierà, such entirety come defined topologico space.

Beyond to Rⁿ following are topologici spaces also:

"^* = "ⁿ ? { - ¥ } ? { ¥ )

you notice that ordered draft of with and that - ¥ and ¥ are not of n but only of the symbols the representatives of the concepts. It is still possible to speak about intorni and in particular it is asserted:

1) around of x remains unchanged that is is open interval (x - ? , x ? ) on the straight one oriented representative ".

2) around of ¥ is the semistraight one that goes from x to ¥ with this last inner point to closing of the interval.

3) around of -¥ is the semistraight one that goes from x to -¥ with this last inner point to closing of the interval.

= "ⁿ ? { ¥ }

It can be thought like a straight one that it comes taken for the two borders and combined in a point that we will call ¥.

Just this description door to say to us that with it is not ordered, is like a wheel where sà who is not itself before.

17) Classification of the points:

It is had with and in "ⁿ , we will say that all that that is not in and, is found in the complementary one of and that is C_and.

To the inside of and the following categories of points are distinguished:

Point interno ž a point says inside to and if its around with beam ? > 0 entire are contained in and. With of the inner points of and it comes indicated with .

(to, b) all the points is inner.

[ to, b) all the points is inner except to

Point of Frontiera ž a point says of frontier if in its around they are contained is elements of and that of C_and. With of the points of frontier of and it comes indicated with .

(to, b) all the points is of frontier

[ to, b) all the points is of frontier

(to, b] all the points is of frontier

External point ž a point says outside to and if its around with beam ? > 0 are entire ontenuto in C_and.

 

Point of accumulazione ž an inner point or of frontier is said of accumulation for and if in its around having beam and > 0 is infinites heads of And with of the points of accumulation of and it comes indicated with .

And its inverse one

Point isolato ž Every point in whose around not there are infinites points of and.

is stung that necessarily they belong to the frontier of and, tasks to the series seguente: 0 it is stretched to 0 but us never does not arrive therefore is a point of accumulation that does not belong to and and the elements of and are all points isolate to you.

In a generalized manner the doubt is that there are or less inner points in the entirety, and if there are the successive dilemma is to understand if they are of accumulation or less.

Viceversa the frontier points are always present in any together but not necessarily they are of the accumulation points.

In reference to the limits they come introduced also the following concepts of topology:

Around right ž the around skillful one of point x₀ is not that interval [ x₀ , x₀ d) with d > 0

Around left ž around left of point x₀ is not that interval (x₀ d , x₀] with d > 0

Point of accumulation right ž One point x₀ says of accumulation skillful if in around skillful its you è at least a point of with various from x_0.

Point of accumulation left ž One point x₀ says of left accumulation if in left its around you è at least a point of with various from x_0.

18) Sets opened, sluices, neither opened neither sluices, opened and sluices:

In function of the topologico space in which they are decreased (that is of the type of points of which they are form) the sets to you can be subdivided in the 3 following categories:

Sets Aperti ž sets is constituted from all inner points (that is with around completely contained in and)

(a,b) with is opened in how much is all inner points.

Sets Chiusi ž sets is not opened. In a generalized manner, every entirety constituted from a n° ended of elements is closed.

In particular whichever together and contained in Rⁿ is closed.

{ to } is an entirety closed in how much its around does not contain no other point therefore cannot be inner point of and.

Sets neither opened neither chiusi ž Are sets that it gives a side are opened and from the other side they are sluices

[ a,b) is not opened why it has not around completely contained in and and of other song is not closed in how much b is not point of frontier also for C_and that therefore it cannot be opened.

Sets open and chiusi ž the only ones sets that they are is opened that sluices are {0}= with empty and "ⁿ,

both opening in how much constituted from all inner points but being one the complementary of the other then one of the 2 must also be closed in how much otherwise sends us in air all the second theory which if an entirety is not opened then is chiuso.

We demonstrate to hour in Italian the following affirmations:

1) and is closed

2) ¶and ? = and

3) every point of accumulation of and belongs to and.

1 demonstrates 2

We want to demonstrate that the frontier of and it is contained or he is equal to and, we leave asserting that a point pertaining to the frontier of and can be or block, and in such case it belongs to and or can be an accumulation point, but an accumulation point that stà on the frontier of and, stà also on the frontier of C_and , but being and closed, like asserts point 1, then point x cannot belong to the C_and and therefore x ? And.

2 demonstrate 3

We want to demonstrate that every point of accumulation of and belongs to And Partiamo from the hypothesis that the points of the frontier of and belong to and, therefore if x are one point of accumulation of and, if stà on the frontier, for how much as soon as asserted, it belongs to and, while if it is stung inner of and, it cannot that belong to and.

3 demonstrate 1

We want to demonstrate that and is closed that is that it contains points that completely is not contained in and, we make demonstrating it that C_and contains solo inner points and therefore it is opened. We take x ?C_E and we say that if its around contained points of and then point of accumulation could be defined for and, but 3) it says that a point to us of accumulation of and ? to and therefore pu² not belonging to the frontier of And Therefore if x ? C_and , must is of its inner point but if C is stung inner then_and is opened and therefore and it is closed.

Closing of E ž calls with this term the union of and with its ¶ frontierand and it is indicated with the symbol .

calls closing for via of the previous theorem that that says to us and is closed if and only if the frontier of and is contained or is equal to and.

19) Limits:

Up to now we have spoken about sets stiche operations, hour we pass to dedicate us to the behavior of the functions, begin characterizing some typical characteristics of the functions applied to with X and having values in Rⁿ

20) limited Functions:

A having function Dominion X and codominio "ⁿ with with of existence To and image f (A)si says limited if it exists in "ⁿ one n° real M such that || f(x) || < = M, " x ?To

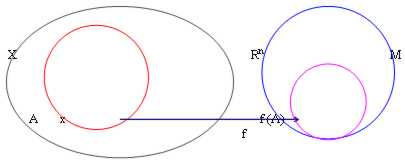
However the example cases are to usual n = 1 (straight) and n = 2 (slowly).

In " following happens:

a function is limited advancedly in To if $ M ? " such that f (x) < = M " x ? To

a function is limited inferiorly in To if $ N ? " such che f (x) > = N " x ? To

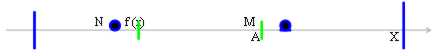
This function says limited in how much is limited is advancedly that inferiorly. From this drift that f(A) with is limited advancedly and inferiorly and that therefore for the thoroughness property (If an entirety A is limited advancedly(inferiorly) that is admits at least a maggiorante(minorante), then it admits also extreme advanced(inferior) that is exists a maggiorante(minorante) that it precedes(follows) the others) admits advanced and inferior end.

In our case the advanced end exists and is M, on condition that you respect the characteristics of the advanced end:

1) " x ? To: f(x) < = M

2) "? > 0 : f(x) > M - ?

that is the advanced end must be smallest of the maggioranti and for how much small is taken a ? and it is embezzled to M, M is not maggiorante why there is a f(x) that he is larger.

If not it had been M we would have assumed sup To = ¥

In our case the inferior end exists and is N, on condition that you respect the characteristics of the inferior end.

1) " x ? To: f(x) > = N

2) "? > 0 : f(x) < N ?

that is the inferior end must be largest of the minoranti and for how much small is taken a ? and the sums to N, N are not minorante why there is a f(x) that it is smaller.

If not it had been N we would have assumed Min To = -¥

We would instead have spoken about maximum or total minimum if M or N respective had made part of To

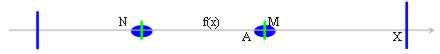
This time the theorem of the thoroughness is useless in fact when we know that f(x) it is limited superiormente(ossia has of the maggioranti), we can say that f(x) it admits advanced end but we do not know analogous if this end is the maximum, for the minimum.

If instead hour we pass to case n = 2 we evidence following:

We pass hour to describe a fundamental concept in the trattazione of the limits, the dependency of our study does not give with of existence but from the codominio and in particular from the image. Often we will find ourselves to observe of the sort of the curves and to take intorni of a point in the I.E. but these intorni they are important single if it considers you like projection arbitrarily on the curve of the true one around chosen in the image.

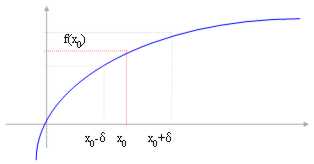
You notice yourself that in this case the function does not have Inf f(A) therefore will assume for default inf f = - ¥

analogous it seems to have Sup f(A) therefore we will not assume for default sup f = ¥

We define therefore:

* relative maximum a point of the image where f(x₀) > = f(x) with x ? around of x₀

* relative the maximum strongly a point of the image where f(x₀) > f(x) with x ? around of x₀

* absolute the maximum a point of the image where f(x₀) = M that is Sup A e f(x) = < M that is Sup To

* relative the minimal a point of the image where f(x₀) < = f(x) with x ? around of x₀

* relative the minimal strongly a point of the image where f(x₀) > f(x) with x ? around of x₀

* absolute the minimal a point of the image where f(x₀) = N that is Inf A e f(x) = < N that is Inf To

In this example:

M = Sup f(A)

N = Inf f(A)

x₂ is stung of total or absolute maximum

x₀ is stung of total or absolute minimum

x₁ is stung of local minimum in how much in around dx f(x_{the 1})<f(x) and in around sx it has smaller values f(x₁)=f(x)

You notice yourself in a generalized manner in the definitions that the immazine calls m.... while correspondent x calls point of m.....

21) Limit of real function of one variable real:

The limit is an instrument, an operation that is proposed to resolve particular preoblemi of the functions like:

* the discontinuity (asymptotes)

* the behavior of the function for values many large or many small

therefore reassuming the limit it is not other that a search of the points of accumulation of the function that is of those points in which the image it is gotten thicker in intorni many small of a value that we will define limit l.

The limit definition I have put to us approximately 2 weeks in order to understand it in intrinsically express how much badly, substantially but he is following:

The equation of the function is observed and it is determined that for it determines values to you of the x calls x to you₀ , the function is not defined. From this observation we pass to deduce on the diagram which it was the value of the function in immediately previous points and following x₀, if such values seem to amass themselves towards an accumulation point, then we say that such point is the limit of the function for x ® x₀ to pact but that:

If we take one around V of l great how much a inezia, as an example around (l - and , l and) with and > 0, we must succeed to find one around of x₀ (with x₀ excluded) as an example (x-d , x d) with d > 0, for which the function is comprised in around V of l.

Such limit calls limit of f(x) for x that stretches to x₀.

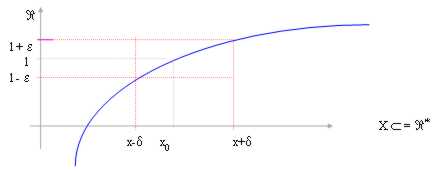
In this case the limit is sure l in how much the function for x-d < x < x d is sure contained in around of l and it can also be observed that l same it is a point of accumulation for x®x₀. That is for x®x₀ the function definitively is comprised in around of l.

Since l ? " we will say also that the function admits limit ended for x ž x₀.

If x₀ had been ¥ then we would have taken the interval in dominion (m, ¥).

If x₀ had been -¥ then we would have taken the interval in the dominion (-¥ , m).

If f(x) ® ¥ for x®x₀ says that the function is an infinite.

If f(x) ® 0 for x®x₀ says that the function is an infinitesimal one and is written o(1).

It is kept property in possession that the function in x does not interest us fà what₀ , a lot that we exclude such point from the limit definition, that note in order to resolve chance where the function is not defined for a determined point.

In this case in which the function it is all in the interval [ l, l and)

One says that the function is limited for excess and it is written:

 

 

In this case in which the function it is all in the interval [ l and , l)

One says that the function is limited for defect and it is written:

 

In this case in which the function it is all in interval (x₀ - d , x₀)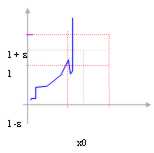

One says that the function admits alone left limit and it is written:

In this case moreover one says that the function is an infinite.

 

In this case in which the function it is all in interval [ x₀ , x₀ d)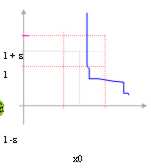

One says that the function admits alone skillful limit and it is written:

In this case moreover one says that the function is an infinite.

22) Property of the limits:

Of the limits we know the following property that can seem banal in how many intuitive, but they hide very more job than demonstration than how much it seems:

Permanence of the sign

This property asserts that if we know that the limit for x ® x₀ has one determined property (as an example is greater of 0), then can say that also f(x) for x ® x₀ it has that determined property.

You notice yourself well that the contrary is not always true, that is if we know that the function for x ® x₀ has one property in that definitively around, then we cannot say that also the limit possesses that property or at least not in strong way, that is we let us make the example of function x² > 0, it we have as limit 0 but 0 is not > 0, that is we we know that the function is definitively > 0 but the limit can be > = 0.

The situation can be resolved taking around of l in which the function is definitively positive.

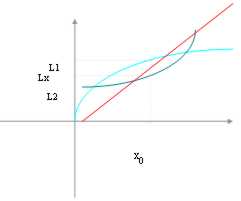
draft that is to take itself and = l - d pertanto 0 < l - ( l - d) < l and therefore f(x) it is

definitively positive and it are also its limit.

But this if the limit is > 0 therefore is not only this the figure adapted.

Demonstration:

Enough to place and = l and then around considered it becomes (0, 2l) and in this around the function it cannot that to be positive.

The limit, if it exists, is only.

It is demonstrated with the intorni, asserting that 2 various limits for x ® x₀ have 2 intorni V₁ and V₂ to i which correspond 2 intorni of x₀ , but the intersection of 2 intorni is still one around of x₀ while the intersection of V₁ and V₂ is empty, that is an absurdity therefore the two limits coincides and the limit is only.

If the function exists the limit then definitively it is limited (admits sup f(x)).

23) Theorem of the comparison:

Having 2 functions, f(x) and h(x) di.le which we know ₂ limitsl ₁ andl and a function g(x) of which we do not know the limit but we know that in around of x₀ are comprised between f(x) and h(x) then we can say that also the limit of g(x) is comprised between l₁ and l₂.

All this assumes exceptional dimensions allorchè l₁ = l₂ in fact in this case must forzatamente be l₁ = l₂ = l₃ and therefore we are resolutions to determine the limit of a function that we would not have known to determine various.

Clearly affinchè this relation is valid around must be smallest possible.

To this theorem we must limit = 1 for x ® 0.

24) Facilitations in the development of the limits:

In the trattazione of limits in which x₀ pu² to belong to "^* the following situations can be met, part di.le which is risolubili, that is:

Following resolves case ¥ l assessing that l same it is not worth -¥ in the which case would be indeterminata ¥ -¥.

1) ¥ limited f(x) inferiorly (possesses a InfX) = ¥

Following resolves the case -¥ l assessing that l same it is not worth ¥ in the which case would be indeterminata -¥ ¥.

2) -advancedly limited ¥ f(x) (it possesses a SupX) = -¥

Following resolves case ¥ - l assessing that l same it is not worth ¥ in the which case would be indeterminata ¥ -¥

3) ¥ - f(x) limited advancedly (possesses a SupX) = ¥

Following resolves the case -¥ - l assessing that l same it is not worth ¥ in the which case would be indeterminata -¥ ¥

4) -¥ - f(x) limited inferiorly (possess a InfX) = -¥

5) ¥ * l = ¥

6) ¥ * - l = -¥

7) -¥ * l = -¥

8) -¥ * - l = ¥

9) 0 * l = 0

10) 1/0 = ¥

11) 1/0^- = -¥

all the cases that do not re-enter in questi call indeterminate shapes and they are resolved with one of following artifixi:

1)

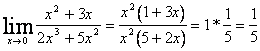
2)

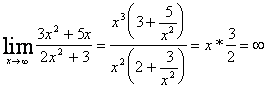
3) Laddove the rationalization of the numerator appears of the fractions is possible.

 

25) Limit of composed functions:

If we have a having function f from X image in one other Y entirety and suppose that this image contains also the limit of the function l for x ® x₀ . A function is had then g(y) that entirety for y associates to the image f(X) a value k inan other®l then is possible to assert that the limit for x®x₀ of g(f(x)) is k.

You notice yourself that compulsorily it must be f(x) ¹ l therefore like was x ¹ x₀.

The demonstration proceeds backwards regarding the design, that is it is asserted that for every around W(k) a V(l) exists around for which the limit definition is respected, for analogous such around V(l) exists around a U(x₀) for which the limit definition is respected. It is in correspondence of this around that the limit of the composed function is respected.

It is observed then that this peculiarity is of great aid in the moment in which we comprise of being able to us to lead back simply to a remarkable limit carrying out a change of variable, the limit but to this point changes, making an example:

we place and we have

26) Limits of functions monotone:

For the functions monotone, the calculation of the limit for x ® x₀ is facilitated in how much such limit corresponds with the Inf of the function or the Sup of the same function to second of the following cases:

1)

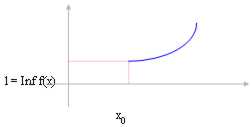If the function is crescent and we only consider around

skillful of x₀ ? "^* then the limit for x ® x₀ corresponds

l = Inf f(x) with the Inf of the function in interval (x₀ , ¥).

x₀

2)

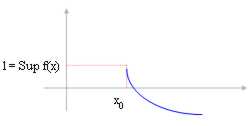If the function is decreasing and we only consider around

skillful of x₀ ? "^* then the limit for x ® x₀ corresponds

l = Sup f(x) with the Sup of the function in interval (x₀ , ¥).

x₀

3)

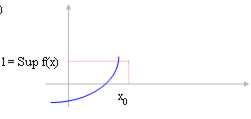If the function is crescent and we only consider around

left of x₀ ? "^* then the limit for x ® x₀ corresponds

l = Sup f(x) with the Sup of the function in interval (-¥ , x₀).

x₀

It is demonstrated observing that the 2 following cases can be introduced:

A) l ? "

for the property of the advanced end:

a) " x ? X ? (- ¥, x₀) : f(x) < = l

b) "? > 0 $ x_? ? X ? (- ¥, x₀): f(x_?) > l - ?

Moreover being the increasing function we can dire: l - ? < f(x_?) < l = Sup f(x)

B) l = ¥

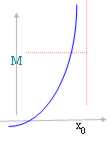
f(x) > M " x ? X ? (- ¥, x₀) and therefore the limit are ¥.

4)

If the function is decreasing and we only consider around

left of x₀ ? "^* then the limit for x ® x₀ corresponds

with the Inf of the function in interval (-¥ , x₀).

 

From these observations on the limits of functions monotone neither they derive analogous on the limits of powers, esponenziali and logarithms and all finalize you to the resolution of limits of the type .

27) Limits of successions to values in ":

A succession is not that a particular type of function from ? in " that it associates that is to every n° natural a value in " second a law it sets up from the same succession. It does not have points of accumulation in ? if not ¥.

To second of as it is behaved the function towards this point of accumulation the 3 cases are distinguished following:

Convergent succession: To stretching of n towards ¥ the succession is become stabilized towards a real value l.

the definition of limit in this case says to us that " ? > 0 to leave from n° the N from which the succession are become stabilized to every n correspond a value of the function that discosta from the limit l less than ?.

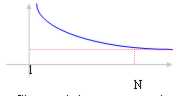
It is observed that a convergent succession also is limited ( ||f(x)|| < = M) based on how much already asserted which consequence that l ? " that as we know it is a tidy field.

It is not per² always true that a limited succession is also convergent, are limited functions between 2 values but that they oscillate in continuation between and an other, therefore they are irregular.

The functions monotone as that one of the figure beyond to being convergent also is limited, the limit is ended if the succession is limited otherwise the limit is ¥.

If the succession stretches to a limit l > 0 then is also it definitively > 0 for n ® ¥, it is not instead true the contrary that is if the succession is definitively > 0, is not said that it it is also its limit which could be that is = 0.

In a generalized manner, we can say that if for n ® ¥ three successions have the following relation of order, to_n [ b_n [ c_n and are to_n that c_n stretches to the limit l, then also b_n stretch to the limit l.

Divergent succession: To stretching of n towards ¥ the succession diverges towards ±¥.

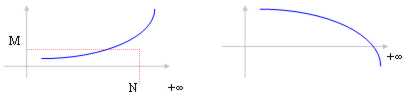
The limit, in the case the succession diverges towards ¥ is same ¥

Irregular succession: To stretching of n towards ¥ the succession is not become stabilized towards some value but oscillates.

28) Theorem âponteâ? and not existence of the limits:

A theorem that represents the conjunction between the considerations made on the limits of the successions and those made on the limits dellle functions, not to case exists this theorem is called âponteâ?. It asserts:

The limit for x ® x₀ of one function f(x) is l >

" succession on _{the 0} abscissas that stretches tox for n ® ¥ , the limit of the function of the succession is l.

In practical we have a succession on the abscissas that stretches to x₀, apply the function to the terms of this succession and find that the limit of this found function is the same one l that we had found for x ® x₀ .

This theorem demonstrates scindendo the > in the 2 members and demonstrating separately:

We demonstrate hour that if ž

It is demonstrated observing that if to_n ® x₀ then beginning from one sure N value in then the limit definition that is on the left comes respected in how much the succession falls in around of x₀ and the corrispettiva function, in around of l.

We demonstrate hour that se ?

It is demonstrated for absurdity asserting that that one on the left is true but the definition of limit to right is false.

To deny the limit definition is equivalent to say that it exists and > 0 such that " d > 0 exists a x_d that it is contained in around of x₀ but the correspondent value of the function exits outside from around of the limit l.

Once asserted this we can assign to x_d i values of the terms of the succession and ossrevare that therefore the succession is contained in around of x₀ but the corresponding function is not contained in around of l, therefore vien contraddetto 2° the member of the equation being you leave yourself from the negation of 1° the member, therefore, the equation therefore as it is written is corrected.

The greater application of this theorem is in the negation of the existence of the limits, in fact the limit is observed that if 2 successions stretch both tox ₀ for n® ¥ but function applied to these 2 successions give 2 various limits, then does not exist.

In practical in order denying the existence of a limit, it is necessary:

1) to find 2 successions that for n® ¥ ₀ stretch tox

2) Verificare that the limit of the function applied to the succession, for n ® ¥ is various for the two successions.

29) Infinites, infinitesimal and confront:

There are of the cases in which the calculation of the limits it leads to indeterminate shapes, as an example: 0/0 oppuranche ¥ / ¥, in these occasions pu² to be useful to the aim of the calculation of the limit, to confront with which speed the two functions become infinitesimal or infinite, that is if one of the 2 is slower regarding the other for which even if both they go to 0 can say that prevailing one, the value of the other not is meaningful and the 0 limit therefore is or ±¥. Analogous if the 2 functions are infinite, could say that one of the 2 goes more quickly to ¥ of the other and therefore the value of the other can be neglected and the limit assumes therefore the 0 value or ±¥ to second of the cases.

Infinitesimal function: it is a function that for x ® x₀ stretch to 0.

Infinite function : is a function that for x ® x₀ stretches to ¥

x₀

The 2 following cases are distinguished:

1) the two functions are both infinitesimal ones for x ® x₀ then the limit of the relationship f(x)/g(x) are worth:

0 in the case f(x) is infinitesimal of advanced order regarding g(x) that is stretches to 0 more quickly.

Tasks to the case where (1 - cos2x) is infinitesimal of advanced order a respect to x that is stretches to 0 more quickly and filler the limit to a case 0/x = 0.

l ? " \{0} if the two functions are infinitesimal of the same order.

tasks to

± ¥ in the case f(x) is infinitesimal of inferior order regarding g(x) that is stretches to 0 more slowly.

Tasks to the where x^to are one infinitesimal one of inferior order regarding sinx therefore the effect of this last one is prevailed 

does not exist the limit in "^*

Tasks to the case limit that does not exist in how much the function continuously second oscillates the law of the breast to ridosso of the origin.

2) the two functions are both infinite ones for x ® x₀ then the limit of the relationship f(x)/g(x) are worth:

0 in the case f(x) is infinite of inferior order regarding g(x) that is stretches more slowly to ¥.

Tasks to the case where x^to are an infinite of inferior order respect to to^x that is filler is stretched more slowly to ¥ the limit to one case x/ ¥ = ¥.

l ? " \{0} if the two functions are infinite of the same order.

tasks to

± ¥ in the case f(x) is infinite of advanced order regarding g(x) that is stretches more fastly to ¥.

Tasks to the where the logarithm is an infinite of advanced order regarding the exponential , therefore prevail the effect of the logarithm. 

the limit in " ^* does not exist

Tasks to the case limit that does not exist in how much the function continuously second oscillates the law of the breast going towards ¥.

30) o(.) :

It is observed that when the limit of one function for x ® x₀ turns out to be 0, says that the function is o(1) to indicate that it is worth a inezia, however is an amount that goes considered in how much perhaps useless in the sums but determining in the products, able to cancel also a giant.

An other I use of the � or piccolo� it is exactly the limit of the relationship between 2 functions, .

If f(x) = g(x) = infinitesimal and we become account that f(x) stretches to zero more quickly that g(x) we cannot say that f(x) = o(g(x)) that is that f(x) is an infinitesimal one of g(x).

In way of all the analogous one,

If f(x) = g(x) = infinite and we become account that f(x) stretches more quicklyto ¥ that g(x) we cannot say che f(x) = o(g(x)) that is that f(x) is an infinite of inferior order regarding g(x).

The potentialities of this instrument but come exalted when in the course of the calculation of some limits some expression of remarkable limit with its value will be able to be replaced o(1) to indicate that for x ® x₀ the value is that one but account of an infinitesimal one must be always held.

31) O(.) :

It is observed that when the limit of one function for x ® x₀ turns out to be l ? " , one says that the function is O(1) to indicate that it assumes a limited value.

An other I use of the � Or grande� it is exactly the limit of the relationship between 2 functions, .

If f(x) = g(x) = infinitesimal and we become account that the relationship stretches to an ended limit we can say that f(x) = O(g(x)) that is that f(x) it is in relation ended with g(x).

In way of all the analogous one,

If f(x) = g(x) = infinite and we become account the relationship it stretches to an ended limit we can say that f(x) = O(g(x)) that is that f(x) it is in relation ended with g(x).

The limit of a relationship between functions for x x ₀ is observed that® when , with f(x) = g(x) = infinitesimal or infinite it is said that f(x) it is asymptotic to g(x), in symbols f(x) ~ g(x).

In the case the 2 functions are of the same order then say that they are asymptotic less than one constant moltiplicativa.

32) infinitesimal Infinites and champion:

Sometimes he will be able to turn out useful to characterize the order of an infinitesimal one in order to simplify the calculation of the limits, comes therefore introduced the concept of the infinitesimal champion, that is we have a relationship between 2 functions of which, g(x) it we to our pleasure introduce and we will come defined infinitesimal champion, in order to know the order of infinitesimal of the others, f(x) we will be enough to know to us which exponent we must elevate g(x) affinchè the relationship has a real limit for

x ® x₀ that is in the interests to us to know the value of to, it represents the order of infinitesimal of the f(x). Analogous fà speech for the infinites.

The choice of the function champion, g(x) happens normally as it follows:

infinitesimal campione: a) x - x₀ if the limit is for x ® x₀ as an example if x ® 0 then the infinitesimal champion is x.

b) 1/x if the limit is for x ® ±¥ as an example if x ® ¥ then the infinitesimal champion is 1/x.

Infinitely campione: a) for x ® x₀^± as an example for x ® 0 g(x) = .

b) x for x ® ±¥ .

In the choice of the infinite champion it must be avoided to impose exponents roots for numbers denied changing champion to you.

33) the n° and:

We have seen as the n° is gained and, it in particular is worth .

In order to reach this result, the is observed that rapporto (where ) for n > 2 he is greater or equal to the 1 that is numerator he is greater or equal to the denominator, therefore from this we deduce that to_n it is a limited succession and increasing in how much the successive element is greater of the previous element.

The is taken then succession , it is confronted with the previous element according to following rapporto the and the function is observed that such relationship is smaller or equal to 1, therefore is decreasing.

But the scope of this second succession was to evidence that to_n it possesses a sup(a_n) and the sup exists in how much

0 < to_n < b_n therefore to_n inequivocabilmente it is limited.

We are arrives you to the conclusion that and it is not other that the point to which 2 successions stretch these, can be returned that is to speak about the concept of n° real like section.