Formule di Analisi Vettoriale
![]()
Ñ(f+g) = Ñ f + Ñg
Ñ · (A+B) = Ñ · A + Ñ · B
Ñ ^ (A+B) = Ñ ^ A + Ñ ^ B
Ñ · (fA) = Ñ f · A + f (Ñ · A)
Ñ ^ (fA) = Ñ f ^ A + f (Ñ ^ A)
Ñ · (A ^ B) = B · (Ñ ^ A) - A · (Ñ ^ B)
Ñ ^ (A ^ B) = (B · Ñ)A - B(Ñ · A) - (A · Ñ)B + A(Ñ · B)
Ñ(A · B) = (B · Ñ)A + (A · Ñ)B + B^(Ñ ^ A) + A^(Ñ ^ B)
Ñ ^ (Ñ f) = 0 Il rotore del gradiente di una funzione scalare è nullo
Ñ · (Ñ ^ A) = 0 La divergenza del rotore di una funzione vettoriale è nulla
Ñ ^ (Ñ ^ A) = Ñ (Ñ · A) - Ñ 2A
Lunghezza di una curva : ![]()
![]()
Ascissa curvilinea : ![]()
Integrale curvilineo di 1ª specie : ![]()
Coordinate baricentro di un filo : 
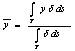

Momento d´inerzia di un filo : ![]()
Volume di un solido di rotazione (Pappo) : ![]()
Integrale curvilineo di 2ª specie : ![]()
Calcolo di un potenziale : ![]()
Versore normale ad una superficie : ![]()
![]()
Piano tangente ad una superficie in un punto : 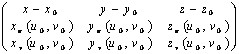 = 0
= 0
Area di una superficie : ![]()
Formula di Guldino : ![]()
Integrale di superficie di una funzione h : ![]()
Teorema di Green nel piano : ![]()
Calcolo aree mediante Green Gauss : ![]()
![]()
Teorema di Stokes : ![]()
Teorema della divergenza di Gauss : ![]()