Linee Accoppiate

1) Equazioni differenziali che descrivono due linee accoppiate :

Se abbiamo due microstriscie affiancate, la linea 1 caratterizzata da una induttanza serie L₁dz e da una capacità parallelo C₁dz mentre la linea 2 caratterizzata da una induttanza serie L₂dz e da una capacità parallelo C₂dz , in virtù della vicinanza avremo poi una mutua induttanza Mdz ed una mutua capacità C_mdz, questa mediante il teorema di Miller può essere suddivisa sulle singole linee, in particolare la capacità parallelo totale della linea 1 diviene  mentre quella sulla linea due diviene  . 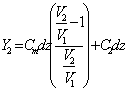L´equazione ai nodi alla linea 1 ci dà mentre quella ai nodi alla linea 2 porta a . In maniera analoga dalle equazioni alle maglie si ottengono   e   .

 

2) Disaccoppiamento delle equazioni differenziali che descrivono due linee accoppiate :

Le ipotesi che si fanno sono le due seguenti :

a)       le due linee accoppiate sono uguali ossia sto utilizzando una struttura simmetrica pertanto L₁ = L₂   e  C₁ = C₂

b)       diagonalizziamo il sistema imponendo ad ogni sezione il cambio di variabili    ,     ,     ,     dove arbitrariamente la linea sopra è la 1 e quella sotto la 2.

Sostituendo le b) nella    e nella   e sommando le due equazioni ottenute si ricava  mentre sottraendo si ottiene  , analogamente per le tensioni poi si ha    e    . Abbiamo pertanto ottenuto un sistema di 4 equazioni differenziali disaccoppiate il che ci consente di trattare le linee come se fossero separate, una relativa al modo even con impedenza caratteristica e costante di fase  e la altra relativa al modo odd con impedenza caratteristica 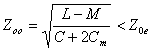e costante di fase    ,  comunque nel seguito si supporrà b_e = b_o .

 

3) Condizioni di chiusura standard per un divisore a linee accoppiate :

Consideriamo 2 linee accoppiate in cui alla porta 1 è applicato un generatore di tensione avente grandezza impressa 2V ed impedenza interna Z₀ mentre tutte le altre porte sono chiuse su di una impedenza Z₀. Le condizioni di chiusura alla sezione d´ingresso 1 sono   e     nelle quali sostituendo le espressioni per il disaccoppiamento    ,     ,     ,     si ottengono   e     . Analogamente le condizioni di chiusura alla sezione d´uscita sono   e     nelle quali sostituendo le espressioni per il disaccoppiamento    ,     ,     ,     si ottengono   e     .

Queste equazioni essendo disaccoppiate ci consentono di trattare separatamente la linea Even e la line a Odd.

 

4) Equazioni di progetto per un divisore a linee accoppiate in condizioni di chiusura standard :

Consideriamo la sola linea Even in quanto le condizioni di chiusura standard imposte sul divisore hanno consentito di disaccoppiare le equazioni, si tratta di un tronco di linea con matrice di trasmissione , fissando ora J_e = J_o = J = p/2 la matrice si semplifica notevolmente ed otteniamo le due equazioni   ,   che sostituite nella condizione  tratta dalla chiusura alla sezione 1 restituiscono  avendo posto   . Si ha poi  ,     e     . I risultati per la linea Odd si ottengono sostituendo e con o nelle equazioni trovate.

5) Condizione di adattamento per accoppiatori direzionali e espressioni delle tensioni alle porte in funzione di Z₀e , Z₀o:

Si ha adattamento se  , sostituendo    e     ed essendo  ,    e   ,     ,    si giunge alla relazione  che consente di scrivere le grandezze alle linee Even ed Odd in forma più semplice, in particolare si ha :

         ;                        ;                                ;             

         ;                        ;                                ;              .

Sostituendo nelle espressioni delle tensioni si ha    ,     il che è logico visto che avevamo un generatore da 2V ed abbiamo imposto la condizione di adattamento,    dove C è il fattore di accoppiamento e viene solitamente espresso in dB,  ossia alla porta 2 il segnale esce sfasato di 90°.

 

6) Parametri di scattering di 2 linee accoppiate in condizioni di chiusura standard e realizzazione accoppiatore a 3dB :

Occorre osservare che tutte le porte sono adattate quindi S₁₁ = S₂₂ = S₃₃ = S₄₄ = 0 in quanto l´onda riflessa è nulla, si deve poi avere S₁₂ = S₂₁ = S₃₄ = S₄₃ = , inoltre S₂₃ = S₃₂ = S₄₁ = S₁₄ =  , infine si ha 

S₃₁ = S₁₃ = S₂₄ = S₄₂ =. Per ottenere un accoppiatore a 3dB occorre semplicemente imporre  Þ .

 

7) Significato dei modi Even ed Odd nel caso di linee accoppiate tipo Stripline :

Si abbiano due piani di massa separati da un dielettrico nel quale sono immersi due conduttori, scegliamo poi un sistema di riferimento x,y rispetto al quale la struttura sia simmetrica, analizziamo separatamente il modo Even ed il modo Odd.

Per il modo Even poniamo V_o = 0 ne deriva che V₁ = V₂ = V_e quindi nel punto di simmetria vi deve essere un massimo oppure un minimo del potenziale pertanto   ne segue che il piano di simmetria è equivalente ad una parete magnetica ideale. In maniera analoga per il modo Odd poniamo V_e = 0 , otteniamo V₁ = V_o   e   V₂ = -V_o quindi nel piano di simmetria il potenziale si deve annullare insieme alla sua derivata quindi il piano di simmetria è equivalente ad una parete elettrica ideale.

 

8) Accoppiatore di Lange :

È un accoppiatore caratterizzato da una banda molto ampia, circa una ottava, è costituito da finger di lunghezza diversa, in particolare quelli corti sono l/4 alle frequenze più alte mentre quelli lunghi sono l/4 alle frequenze più basse. Una caratteristica importante è che il modello che è stato sviluppato funziona perfettamente tuttavia vi sono delle difficoltà a realizzare accoppiatori a 3dB con questa geometria.

 

9) Matrice di trasmissione per linee accoppiate chiuse su un aperto :

Per calcolare la matrice di trasmissione passiamo per la matrice Z, in particolare consideriamo due linee di trasmissione accoppiate, una con un segnale che entra alla porta 1 mentre la porta 4 è chiusa su di un aperto, la altra con il segnale che entra alla porta 2 mentre la porta 3 è chiusa anche essa su di un aperto.

Imponendo la condizione di chiusura  alla sezione 0 d´ingresso si ottiene che  mentre imponendo la condizione di chiusura  alla sezione J d´uscita si ottiene che . Sostituendo si ha    e .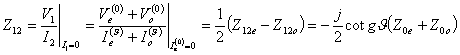

Da queste si può ottenere   e     .

 

10) Matrice di trasmissione del filtro commensurato :

Per calcolare la matrice di trasmissione passiamo per la matrice Z, in particolare consideriamo due linee di trasmissione accoppiate, una con un segnale che entra alla porta 1 ed esce dalla porta 2 mentre la altra alla porta 3 è chiusa su un corto circuito mentre alla porta 4 è chiusa su di un aperto, evidentemente il comportamento sarà di tipo passabasso.

Imponendo la condizione di chiusura  alla sezione 0 d´ingresso si ottiene che  mentre imponendo la condizione di chiusura  alla sezione J d´uscita si ottiene che . Sostituendo si ha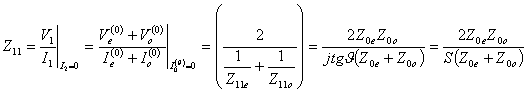  

  e 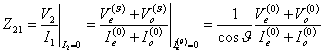. Da queste si può ottenere  ,  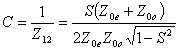     mentre per ricavare B partiamo da  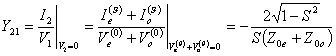 pertanto  .