Stima dello spettro di potenza
1) Parametri statistici di un processo aleatorio stazionario :
![]() valor medio
valor medio
![]() media temporale
media temporale
![]() media temporale di ogni sequenza campione
media temporale di ogni sequenza campione
![]() varianza
varianza
![]() autocovarianza
autocovarianza
![]() densità spettrale di potenza
densità spettrale di potenza
2) Stima della media :
![]()
rappresenta una stima accurata soltanto se N è un numero molto elevato.
3) Stimatore buono :
È uno stimatore per il quale è elevata la probabilità che la stima sia prossima al parametro da stimare, ossia la densità di probabilità deve essere stretta e concentrata intorno al valore vero.
4) Polarizzazione di uno stimatore :
È la differenza tra il valore vero a del parametro ed il valore atteso della stima ![]() .
.
5) Varianza di uno stimatore :
![]()
6) Errore quadratico medio di uno stimatore :
![]()
7) Stimatore consistente :
È uno stimatore per il quale la polarizzazione e la varianza tendono entrambe a zero al crescere del numero di osservazioni.
8) Stima a massima verosimiglianza :
Stima a massima verosimiglianza del valor medio mx di un processo aleatorio
![]() è la media campionaria caratterizzata da una varianza
è la media campionaria caratterizzata da una varianza ![]() e da polarizzazione nulla quindi dato che al crescere di N la varianza diminuisce si ha che la media campionaria è uno stimatore consistente.
e da polarizzazione nulla quindi dato che al crescere di N la varianza diminuisce si ha che la media campionaria è uno stimatore consistente.
Stima a massima verosimiglianza della varianza di un processo aleatorio
![]() , nel caso mx non sia noto può essere sostituito nell´espressione dalla sua stima, si ha però che il valore atteso della varianza campione non coincide con la varianza per N piccoli presentando pertanto una polarizzazione che scompare per N®¥ . La varianza della varianza campione è
, nel caso mx non sia noto può essere sostituito nell´espressione dalla sua stima, si ha però che il valore atteso della varianza campione non coincide con la varianza per N piccoli presentando pertanto una polarizzazione che scompare per N®¥ . La varianza della varianza campione è ![]() pertanto si ha che la varianza campione è una stima consistente.
pertanto si ha che la varianza campione è una stima consistente.
9) Stima della sequenza di autocorrelazione di un processo a media nulla:
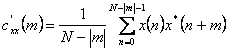
si tratta di uno stimatore consistente in quanto non è polarizzato e la sua varianza tende a zero per N®¥ .
10) Stime della sequenza di autocorrelazione di un processo a media nulla:
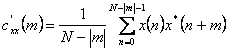
si tratta di uno stimatore consistente in quanto non è polarizzato e la sua varianza tende a zero per N®¥ . SI ha però che se m®N la varianza della stima cresce notevolmente rendendo la stima stessa non utile, tale inconveniente non è invece presente nella stima ![]() .
.
11) Periodogramma di una sequenza bianca :
![]()
esso è una stima polarizzata dello spettro di potenza Pxx(w) in quanto il suo valore atteso non coincide con la trasformata di Fourier della autocorrelazione jxx(m), questo risultato si ottiene sia considerando il periodogramma come Trasformata di Fourier della stima cxx(m) che della stima c´xx(m). La varianza del periodogramma è 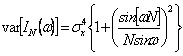 e non tende a 0 per N®¥ quindi il periodogramma non è una stima consistente, in particolare si hanno oscillazioni crescenti al crescere di N.
e non tende a 0 per N®¥ quindi il periodogramma non è una stima consistente, in particolare si hanno oscillazioni crescenti al crescere di N.
12) Periodogramma di un rumore colorato :
![]()
dove ![]() è il periodogramma di un rumore bianco e Pxx(w) è la densità spettrale di potenza del rumore colorato. La varianza del periodogramma è
è il periodogramma di un rumore bianco e Pxx(w) è la densità spettrale di potenza del rumore colorato. La varianza del periodogramma è  , pertanto il periodogramma non è uno stimatore consistente e presenta delle oscillazioni notevoli attorno al valore vero dello spettro.
, pertanto il periodogramma non è uno stimatore consistente e presenta delle oscillazioni notevoli attorno al valore vero dello spettro.
13) Metodo di Bartlett per la stima dello spettro :
Consiste nel suddividere la sequenza dati x(n) in K segmenti di M campioni ciascuno, si calcolano i K periodogrammi nella forma 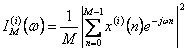 essi sono tra loro indipendenti e pertanto la stima dello spettro assume l´espressione
essi sono tra loro indipendenti e pertanto la stima dello spettro assume l´espressione ![]() , il suo valore atteso è la convoluzione dello spettro vero Pxx(w) con la trasformata di Fourier della funzione finestra rettangolare corrispondente ad un periodogramma calcolato su N campioni., la varianza tende a 0 al crescere del numero di campioni N pertanto la stima di Bartlett è consistente. Si ha che al crescere del n° dei periodogrammi la varianza diminuisce ma anche la risoluzione dello spettro.
, il suo valore atteso è la convoluzione dello spettro vero Pxx(w) con la trasformata di Fourier della funzione finestra rettangolare corrispondente ad un periodogramma calcolato su N campioni., la varianza tende a 0 al crescere del numero di campioni N pertanto la stima di Bartlett è consistente. Si ha che al crescere del n° dei periodogrammi la varianza diminuisce ma anche la risoluzione dello spettro.
14) Metodo delle finestre per la stima dello spettro :
Si considera il periodogramma smussato ![]() avente valore atteso
avente valore atteso ![]() e varianza
e varianza 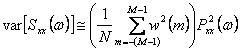 da cui si osserva che il periodogramma è asintoticamente non polarizzato.
da cui si osserva che il periodogramma è asintoticamente non polarizzato.
15) Metodo di Welch :
È una modifica del metodo di Bartlett, in sostanza la finestra w(n) viene applicata direttamente ad ogni sottosequenza di dati ottenuta dalla sequenza d´ingresso x(n) , si ottengono pertanto K periodogrammi modificati 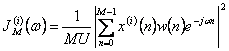 dove
dove ![]() è un fattore di normalizzazione necessaario affinché la stima
è un fattore di normalizzazione necessaario affinché la stima ![]() sia asintoticamente non polarizzata.
sia asintoticamente non polarizzata.
16) Applicazione della FFT ai metodi di Bartlett o di Welch per la stima dello spettro di potenza :
Occorre calcolare per ogni sottosequenza 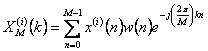 mediante un algoritmo di FFT, si calcolano poi
mediante un algoritmo di FFT, si calcolano poi ![]() e si sommano una alla altra sino a i=K infine il risultato và diviso per KMU.
e si sommano una alla altra sino a i=K infine il risultato và diviso per KMU.
17) Applicazione della FFT al calcolo di stime della correlazione :
Un primo procedimento è :
a) si costruisce una sequenza di L punti aggiungendo a x(n) (M-1) zeri
b) si calcola la DFT su L punti 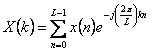 con k = 0,1, … , L – 1
con k = 0,1, … , L – 1
c) si calcola la DFT inversa su L punti 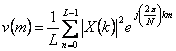 con m = 0,1, … , L – 1
con m = 0,1, … , L – 1
d) ![]() con m = 0,1, … , M – 1
con m = 0,1, … , M – 1
Un secondo procedimento è invece :
a) si costruisce la sequenza ![]() e se ne calcola la trasformata su 2M punti
e se ne calcola la trasformata su 2M punti