Segnali e sistemi a tempo discreto
1) Segnali a tempo discreto :
Sono definiti su di un insieme discreto di tempi, possono assumere valore qualsiasi x(n), sono anche chiamati sequenze.
2) Energia di una sequenza :
![]()
3) Descrizione matematica di un sistema :
È una trasformazione univoca che mappa una sequenza d´ingresso x(n) in una sequenza d´uscita y(n) = T [ x(n) ]
4) Sistema invariante alla traslazione :
Se y(n) è la risposta ad x(n) allora y(n-k) è la risposta a x(n-k).
5) Somma di convoluzione :
![]()
6) Sistema stabile :
È un sistema per cui ogni ingresso limitato provoca un´uscita limitata, i sistemi LTI sono stabili se ![]()
7) Equazione lineare alle differenze a coefficienti costanti :
![]()
8) Sistema FIR :
È un sistema avente una risposta all´impulso di durata finita, è descritto da un´equazione alle differenze a coefficienti costanti ![]() con N = 0 .
con N = 0 .
9) Sistema IIR :
È un sistema avente una risposta all´impulso di durata infinita, è descritto da un´equazione alle differenze a coefficienti costanti ![]() con N > 0 .
con N > 0 .
10) Trasformata di Fourier di una sequenza x(n) :
![]()
si osservi che nel caso di una sequenza x(n) reale, la parte reale della sua trasformata di Fourier è una funzione pari mentre la parte immaginaria è una funzione dispari.
11) Antitrasformata di Fourier di una sequenza x(n) :
![]()
12) Aliasing di un segnale campionato :
Si presenta quando il periodo di campionamento è troppo lungo per cui le repliche traslate vengono a sovrapporsi.
13) Relazione tra la trasformata di Fourier a tempo continuo e la trasformata di Fourier di una sequenza derivata mediante campionamento :
![]()
quindi lo spettro del segnale campionato è periodico e coincide con lo spettro del segnale analogico soltanto in (-p ,p) a patto che sia ![]() .
.
14) Formula di interpolazione per ricostruire il segnale a tempo continuo xa(t) a partire dai suoi campioni :
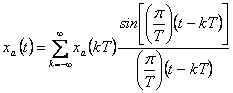
per giungere ad essa si parte dall´ipotesi che non vi sia aliasing .