Filtres aux micro-ondes
Commensurati de filtres pas
1) les options de progettuali pour des filtres passent aux constantes distribuées :
) filtre pas le commensurati qui emploient la ligne dispositifs qu'elles n'ont pas toute la même longueur
b) filtre le commensurati dans lequel ont pour être une question de la ligne ayant toute la même longueur que la transformation de fréquence est atteint au moyen d'une
c) J'emploie de l'image de paramètres afin de caractériser une base sûre de cellules, cette approche est tombé dans la désuétude
2) PLR :
Le rapport perdu par puissance est le rapport entre la
puissance de Pdedans dans le
revenu au filet et la puissance PT transmise à la cargaison, a en particulier 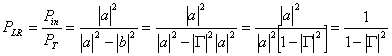 , pour le filtre passe-bas
de P LR vaut la peine 1 jusqu'à ce
qu'à la fréquence de la coupe commandiez dedans alors l'étirage au ¥ dans le plus ou la manière
moins raide à la deuxième qui le filtre est idéal ou vrai.
, pour le filtre passe-bas
de P LR vaut la peine 1 jusqu'à ce
qu'à la fréquence de la coupe commandiez dedans alors l'étirage au ¥ dans le plus ou la manière
moins raide à la deuxième qui le filtre est idéal ou vrai.
3) typologie d'approximation :
PLR dans le cas de
l'approximation de Butterworth vaut la peine 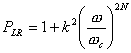 et a
donc la forme d'une parabole centrée dans W = 0. Dans le cas de l'approximation de Chebyshev à
la place
et a
donc la forme d'une parabole centrée dans W = 0. Dans le cas de l'approximation de Chebyshev à
la place 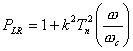 est eu où
est eu où ![]() est le
polinomi de Chebyshev.
est le
polinomi de Chebyshev.
4) réalisation des lowpass de filtres :
La typologie des lowpass de filtres qu'ils réalisent que les approximations de Butterworth et de Chebyshev sont différentes au deuxième ce il est N égal ou N inégal mais après toute l'ébauche des filets de balance constitués à partir du parallèle de capacités et des séries d'inductances a toujours alimenté d'un générateur doté de tension de rigidité intérieure et d'écluses sur une résistance unitaire. Nous devons changer ce filet en concentrés de paramètres valides à la très basse fréquence à vous dans un filet aux paramètres distribués valides aux fréquences au moins un certain gigahertz, afin d'obtenir qui sont deux approches :
) les inductances elles viennent
remplacé avec un dispositif court de ligne et à Z élevéC (…donc une ligne beaucoup
de poignée) tandis que les capacités mettent en parallèle à qui
matrice de transmission ![]() est venue a remplacé avec
un dispositif d'avoir la ligne q petite et ZC petit,
dans un tel cas est eu en fait
est venue a remplacé avec
un dispositif d'avoir la ligne q petite et ZC petit,
dans un tel cas est eu en fait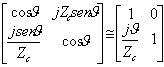 de quel égaler les
deux matrices que j'obtiens
de quel égaler les
deux matrices que j'obtiens ![]() a donc
a donc ![]() où n il est la vitesse
de propagation sur la ligne. Le vrai est incognito mais la
longueur l de la ligne, elle vaut la peine
où n il est la vitesse
de propagation sur la ligne. Le vrai est incognito mais la
longueur l de la ligne, elle vaut la peine ![]() .
.
b) se rappelant que la matrice de Z de
la ligne notation est  et étant note les relations
entre les éléments d'un filet à T et les coefficients de sa matrice
de Z qu'il est obtenu pour les stiffnesses longitudinaux de la même
chose
et étant note les relations
entre les éléments d'un filet à T et les coefficients de sa matrice
de Z qu'il est obtenu pour les stiffnesses longitudinaux de la même
chose ![]() tandis que pour la rigidité en coupe il est
eu simplement
tandis que pour la rigidité en coupe il est
eu simplement ![]() . Q supposant petit et pensant pour réaliser Zà et Zb avec une inductance, j'obtiens pour elle
. Q supposant petit et pensant pour réaliser Zà et Zb avec une inductance, j'obtiens pour elle ![]() imaginer analogue d'expression pour réaliser Zc avec une capacités que j'obtiens pour
lui
imaginer analogue d'expression pour réaliser Zc avec une capacités que j'obtiens pour
lui ![]() . Ce modèle est mené de nouveau à
celle-là des capacités simples dans les marques de cas l'hypothèse
de Zc petite. De la
manière analogue il peut penser à un filet à p que l'inductance est comportée comme une
. Ce modèle est mené de nouveau à
celle-là des capacités simples dans les marques de cas l'hypothèse
de Zc petite. De la
manière analogue il peut penser à un filet à p que l'inductance est comportée comme une
Le filtre d's'avérer est donné de la série de dispositifs serrés de ligne qui simulent l'inductance et les dispositifs larges de la ligne qui simulent les capacités, dans la vérité alors devraient également pour considérer vous ont orné dû aux transitions brusques.
5) réalisation des filtres passe-bandes :
Afin de passer des lowpass de Chebyshev ou de Butterworth
aux correspondants passe-bandes la transformation est colombe  utilisée que W'est la
fréquence des lowpass et W c'est
la fréquence du passe-bande d'ailleurs
utilisée que W'est la
fréquence des lowpass et W c'est
la fréquence du passe-bande d'ailleurs![]() . Le
circuita les effectuent de ce pu² de transformation pour s'obtenir qui
est uguagliando
. Le
circuita les effectuent de ce pu² de transformation pour s'obtenir qui
est uguagliando 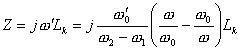 la rigidité de chaque Lactuel l'inductance k dans les lowpass avec la rigidité de la série
la rigidité de chaque Lactuel l'inductance k dans les lowpass avec la rigidité de la série ![]() d'une inductance et
d'une inductance et ![]() des
capacités
des
capacités 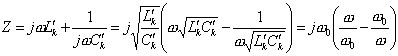 , obtient
, obtient ![]() et
et ![]() . En raisonnement de manière sur les admittances on
obtient que les capacités aux lowpass transforment dans le parallèle
d'une
. En raisonnement de manière sur les admittances on
obtient que les capacités aux lowpass transforment dans le parallèle
d'une ![]() capacités et d'une
capacités et d'une
![]() inductance.
inductance.
6) Invester de rigidité et invester d'accès :
L'ébauche des filets qui concourent nous pour réaliser
les filets non proportionnés passe-bandes avec les paramètres
distribués en particulier l'invester de rigidité est un filet qui
éclusent sur une cargaison bde Z présente dans le revenu que ![]() une
rigidité tandis que l'invester d'accès est un filet qui éclusent
sur une cargaison bde Y présente dans l'accès du revenu un
une
rigidité tandis que l'invester d'accès est un filet qui éclusent
sur une cargaison bde Y présente dans l'accès du revenu un ![]() .
Les éléments de la matrice de Z de l'invester de rigidité se
gagnent
.
Les éléments de la matrice de Z de l'invester de rigidité se
gagnent ![]() d'imposer en fait le ce il est égal
d'imposer en fait le ce il est égal ![]() à puis obtient qui doit êtreZ 11 =22 Z = 0
à puis obtient qui doit êtreZ 11 =22 Z = 0 ![]() et, se rappelant la relation entre
les éléments de la matrice de Z et ceux de la matrice de
transmission on l'a que que pour elle à = D = 0.
et, se rappelant la relation entre
les éléments de la matrice de Z et ceux de la matrice de
transmission on l'a que que pour elle à = D = 0.
Les éléments de la matrice de Y de l'invester d'accès
s'obtiennent ![]() de l'égalité, nécessité eux-mêmes
soient en fait Y eu11 = ede Y 22 = 0
de l'égalité, nécessité eux-mêmes
soient en fait Y eu11 = ede Y 22 = 0 ![]() également dans ce cas-ci donc pour la matrice
correspondante de transmission ont eux-mêmes = D = 0.
également dans ce cas-ci donc pour la matrice
correspondante de transmission ont eux-mêmes = D = 0.
7) réalisation pratique d'un invester d'accès :
L'invester d'accès n'est employé dans la réalisation
pas du commensurati passe-bande dans la bandede m, une réalisation possible est donné
de la cascade d'un dispositif d'avoir la ligne rigidité 0Z et longueurs f/2, une série d'accès ![]() de valeur et de s'accorder au dispositif de la
ligne égale à la précédente. La matrice de s'avérer la
transmission est le produit des trois matrices, et nous il des
intérêts de placer A=0 qu'il est l'une des conditions afin de
réaliser un invester d'accès, obtient
de valeur et de s'accorder au dispositif de la
ligne égale à la précédente. La matrice de s'avérer la
transmission est le produit des trois matrices, et nous il des
intérêts de placer A=0 qu'il est l'une des conditions afin de
réaliser un invester d'accès, obtient ![]() tandis que
le placement
tandis que
le placement ![]()
![]() est obtenu et donc
est obtenu et donc 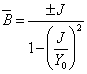 .
.
8) la réalisation des passages se réunissent avec l'invester de rigidité :
En parallèle à la cargaison RL du passe-bande nous avons un parallèle résonnant
de cellules constitué à partir ![]() et
et ![]() la suite d'une série résonnante de cellules constituée
à partir
la suite d'une série résonnante de cellules constituée
à partir ![]() et
et ![]() , la rigidité du
revenu de ce sottorete est :
, la rigidité du
revenu de ce sottorete est : 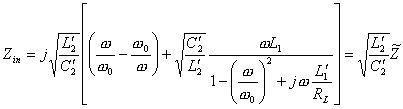 , uguagliamo elle à
la rigidité
, uguagliamo elle à
la rigidité  du revenu d'un filet constitué à
partir de la cargaison 0Lde R , un invester de la rigidité K10 , des séries résonnantes L 01C 01de
cellules , un invester de la rigidité K21 et des deuxièmes séries
résonnantes 02
LC 02de cellules , obtiennent les valeurs des investers e
du revenu d'un filet constitué à
partir de la cargaison 0Lde R , un invester de la rigidité K10 , des séries résonnantes L 01C 01de
cellules , un invester de la rigidité K21 et des deuxièmes séries
résonnantes 02
LC 02de cellules , obtiennent les valeurs des investers e 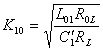 qui est e
qui est e  .
.
Il est possible de retourner simplement vers le
générateur remplaçant la résistance R Lde cargaison avec  une
rigidité dans le schematizzazione précédent sans investers et en
remplaçant la résistance 0Lde R avec une rigidité
une
rigidité dans le schematizzazione précédent sans investers et en
remplaçant la résistance 0Lde R avec une rigidité 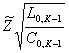 dans le
schematizzazione avec des investers, obtenez donc les valeurs des
investers de rigidité, en particulier
dans le
schematizzazione avec des investers, obtenez donc les valeurs des
investers de rigidité, en particulier  e
e 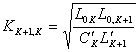 . Nous passons l'heure pour analyser la cellule
résonnante
. Nous passons l'heure pour analyser la cellule
résonnante ![]() et
et ![]() plus près le
générateur et son résistance intérieure Rg , dans le circuit avec des investers
que nous aurons la cellule résonnante
plus près le
générateur et son résistance intérieure Rg , dans le circuit avec des investers
que nous aurons la cellule résonnante ![]() et
et ![]() et la résistance intérieure
et la résistance intérieure ![]() du
générateur, nous bidon donc au moyen d'un gain de proportion la
rigidité intérieure du générateur
du
générateur, nous bidon donc au moyen d'un gain de proportion la
rigidité intérieure du générateur ![]() , s'il est
divers de la valeur souhaitée assez simplement pour insérer un
invester ultérieur qui disparaît inséré également dans le cas de
N inégal pour lequel la cellule résonnante plus voisine au
générateur est de type parallèle. Elles restent heure à
réaliser que la série de risonanti avec des longues lignes de la
transmission l/2 obtient
, s'il est
divers de la valeur souhaitée assez simplement pour insérer un
invester ultérieur qui disparaît inséré également dans le cas de
N inégal pour lequel la cellule résonnante plus voisine au
générateur est de type parallèle. Elles restent heure à
réaliser que la série de risonanti avec des longues lignes de la
transmission l/2 obtient ![]() à partir de quel pu² pour déterminer la rigidité
caractéristique de ces lignes.
à partir de quel pu² pour déterminer la rigidité
caractéristique de ces lignes.
9) la réalisation des passages se réunissent avec l'invester de rigidité :
De la manière complémentaire combien de fait avec les
investers de rigidité, le passe-bande net peut être réalisé
qu'employer d'avoir des investers des espaces des valeurs 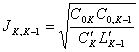 e
e 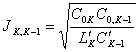 d'accès hors de vous des circuits de
risonanti parallèles qui peuvent être réalisez à vous au moyen de
de longues lignes l/2, en
particulier l'uguagliando que les dérivés respectent à W des éléments C des matrices de
transmission est atteint
d'accès hors de vous des circuits de
risonanti parallèles qui peuvent être réalisez à vous au moyen de
de longues lignes l/2, en
particulier l'uguagliando que les dérivés respectent à W des éléments C des matrices de
transmission est atteint ![]() la relation qui concourt
pour déterminer la rigidité caractéristique de la longue ligne l/2.
la relation qui concourt
pour déterminer la rigidité caractéristique de la longue ligne l/2.
10) capacitivo d'espace de bande de passage de filtres :
Cette réalisation emploie des investers de rigidité
constitués à partir de 2 dispositifs d'inframmezzati de lignef /2 des
capacités, les deux investers sont alors séparés à vous d'un
parallèle de risonatore réalisé avec un dispositif de ligne le long de l/2 et ayant la rigidité
caractéristique Zc qui est
égale placé à Z0 , les
valeurs des capacités peuvent être gain à vous avec
![]() la formule peuvent donc déterminer
la formule peuvent donc déterminer  l'être la série décrite résonnante de
l'être la série décrite résonnante de ![]() tandis que le parallèle résonnant il est décrit
tandis que le parallèle résonnant il est décrit ![]() d'où gle K est les
coefficients des lowpass du départ.
d'où gle K est les
coefficients des lowpass du départ.
Dans le fattispecie pour le premier invester  est eu tandis que pour le prochain invester au générateur
est eu tandis que pour le prochain invester au générateur  dans le cas de N inégal et
dans le cas de N inégal et 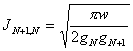 dans
le cas de N égal est eu.
dans
le cas de N égal est eu.
Vous notez que le J est possible pour déterminer le
suscettanze des investers au moyen 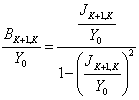 de la relation
et
de la relation
et ![]() les longueurs en suivent que le suscettanze sont
séparés de longs dispositifs de ligne
les longueurs en suivent que le suscettanze sont
séparés de longs dispositifs de ligne 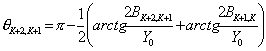 . Le
problème principal de ce filtre est les dimensions excessives.
. Le
problème principal de ce filtre est les dimensions excessives.
11) bande de passage de filtres aux lignes couplées :
La réunir fortement est eue qu'un croisillon des
investers d'accès sépare à vous d'un dispositif de ligne le long de l/2 (…la
matrice de la transmission de la structure a 
 e) est équivalente à des lignes couplées écluses sur un
ouvert de côtés opposés (… caractérisés
e) est équivalente à des lignes couplées écluses sur un
ouvert de côtés opposés (… caractérisés ![]()
![]() de e).
de e).
Les égalant entre les équations de à et les équations
de B encore moins de leurs dérivés il est atteints les deux
équations du plan ![]() e
e ![]() .
.
12) la réalisation pratique du microruban filtre passe-bande :
Partie des deux fréquences de la coupe à â?"3dB du
passe-bande, du f1 et du f2 , les gains la fréquence les
centre ![]() et par la transformation dans la fréquence
le W est déterminé des lowpass, il avec à la pente souhaitée du filtre
concourt pour déterminer l'ordre de N et donc pour extraire à partir
des tables les valeurs des membres il des concentrés vous du filtre
de Butterworth. À ce point que nous avons des investers de N 1
sépare à vous des longues lignes l/2 et ayant la rigidité Z0 , le coefficient du premier invester trouve avec la formule
et par la transformation dans la fréquence
le W est déterminé des lowpass, il avec à la pente souhaitée du filtre
concourt pour déterminer l'ordre de N et donc pour extraire à partir
des tables les valeurs des membres il des concentrés vous du filtre
de Butterworth. À ce point que nous avons des investers de N 1
sépare à vous des longues lignes l/2 et ayant la rigidité Z0 , le coefficient du premier invester trouve avec la formule 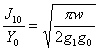 tandis que ceux de restant avec elle
tandis que ceux de restant avec elle 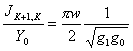 nous peuvent mettre en application les deux réalisations
suivantes :
nous peuvent mettre en application les deux réalisations
suivantes :
) pour que le filtre l'entaille permet le suscettanze à vous sont immédiatement calculable et d'elles les capacités et la distance entre deux capacités successives.
b) Pour le filtre aux lignes couplées du gainZ 0e et Z immédiatement 0o de JK 1,de K qu'ils déterminent les largeurs des lignes tandis que les longueurs sont tous les pairs à l/2.
Filtres de Commensurati
13) transformation de Richard :
C'est une transformation périodique dans combien emploie
la tangente, 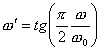 est eu où W'il est la pulsation dans le filtre passe-bas
tandis que W il est la
pulsation dans les passages se réunissent, du repos dans la vérité
également dans le cas des filtres de commensurati n'étaient pas
obtenus des réponses périodiques même si nous avons analysé au
pass-band simple de comportement.
est eu où W'il est la pulsation dans le filtre passe-bas
tandis que W il est la
pulsation dans les passages se réunissent, du repos dans la vérité
également dans le cas des filtres de commensurati n'étaient pas
obtenus des réponses périodiques même si nous avons analysé au
pass-band simple de comportement.
L'usefullness de cette transformation est qu'il concourt pour réaliser une capacités CK avec un moignon ouvert le long de l/4 et avoir la rigidité caractéristique CK tandis qu'une inductance de la valeur LK vient réalisé avec un moignon en bref le long de l/4 et avoir la rigidité caractéristique LK .
Le problème qui monte est celui dans le filtre passe-bas de filtres duquel la partie afin de s'obtenir des passages pour réunir les inductances est en série et donc elles ne peuvent pas être remplacées avec le moignon dans combien le moignon coûte toujours en parallèle, parce que les capacités pas là sont à la place des problèmes et elles qu'il sera essayé du ricondursi au moyen de moi l'emploient des éléments unitaires de Kuroda.
14) élément unitaire de Kuroda :
C'est des portes d'un dispositif deux caractérisées
d'une rigidité caractéristique Z1 et ![]() d'une longueur donc à la fréquence
du travail qu'elle est sensiblement l/4, sa matrice de transmission est gagné pour laisser de
la matrice de la transmission d'un dispositif de ligne de transmission
le long de q
d'une longueur donc à la fréquence
du travail qu'elle est sensiblement l/4, sa matrice de transmission est gagné pour laisser de
la matrice de la transmission d'un dispositif de ligne de transmission
le long de q  c'est-à-dire, dans lui le pu² pour remplacer
c'est-à-dire, dans lui le pu² pour remplacer ![]() l'infatti
l'infatti  suit une partie à partir
suit une partie à partir ![]() dont
dont ![]() donc obtient la valeur à
nous de cosq. Du repos
est eu
donc obtient la valeur à
nous de cosq. Du repos
est eu ![]() également donc la matrice de transmission
devient
également donc la matrice de transmission
devient  .
.
15) équivalences qui sont impliquées les éléments unitaires de Kuroda :
Deux équivalences suivantes peuvent être démontrées :
) un élément unitaire avec la rigidité 1de Z ayant dans les capacités C parallèle du revenu un est équivalent à un élément unitaire avec la rigidité Z2 ayant dans l'inductance L série de l'évasion une
La matrice de la transmission de la structure
avec les capacités est 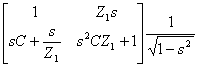 tandis que celui-là de la
structure avec l'inductance est
tandis que celui-là de la
structure avec l'inductance est 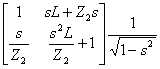 les limites à est
égal tandis qu'à partir de la limite de B nous obtenons
les limites à est
égal tandis qu'à partir de la limite de B nous obtenons ![]() la relation, de la limite C
la relation, de la limite C ![]() la relation
et finalement de la limite de D la relation
la relation
et finalement de la limite de D la relation ![]() , à ce
point est possible les deux manières suivantes :
, à ce
point est possible les deux manières suivantes :
· Nous supposons que vous noter Z1 et C et nous placent ![]() ,
remplaçant dans
,
remplaçant dans ![]() obtient
obtient ![]() tout en
remplaçant dans
tout en
remplaçant dans ![]() il est obtenu
il est obtenu ![]()
· Nous supposons que vous noter 2Z et L et nous
placez ![]() , remplaçant dans
, remplaçant dans 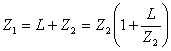 obtient
obtient ![]() tout en remplaçant dans
tout en remplaçant dans ![]() il est
obtenu
il est
obtenu ![]()
b) un élément unitaire avec la rigidité de Zun 1 ayant dans l'inductance L série de revenu est équivalent à un élément unitaire ayant dans les capacités C parallèle de l'évasion une
La matrice de la transmission de la structure
avec l'inductance est 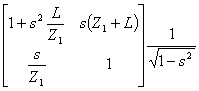 tandis que celui-là de la
structure avec les capacités est
tandis que celui-là de la
structure avec les capacités est  les limites de D
est égal tandis qu'à partir de la limite à nous obtenez
les limites de D
est égal tandis qu'à partir de la limite à nous obtenez ![]() la relation, de la limite de B
la relation, de la limite de B ![]() la
relation et finalement de la limite C la relation
la
relation et finalement de la limite C la relation ![]() ,
à ce point est possible les deux manières suivantes :
,
à ce point est possible les deux manières suivantes :
· Nous supposons que vous noter Z1 et L et nous placent ![]() ,
remplaçant obtient
,
remplaçant obtient ![]() e
e ![]()
· Nous supposons que vous noter 2Z et C et nous
placez ![]() , le remplacement de lui est obtenu
, le remplacement de lui est obtenu ![]() et
et ![]()
16) la réalisation des filtres passe la bande au moyen des éléments unitaires de Kuroda :
Nous considérons le filtre passe-bas de 4° l'ordre constitué à partir de 2 séries d'inductances et de 2 capacités parallèles, nous nous insérons pour monter un élément unitaire de Kuroda avec la rigidité Z0 , il pas modification l'amplitude de l'évasion, puis transformons le courrier de série d'inductance à son évasion dans un courrier de parallèle de capacités à son revenu au bâti duquel heure se joint à un autre U.E. doit leur évasion des capacités en parallèle et vient transforme dans d'autres 2 U.E. à vous ayant dans le revenu par série d'inductance, à ce point un autre U.E. se joint au bâti et il emploie pour tous et trois la transformation qui concourt pour passer d'un U.E. avec une série d'inductance à son évasion à un U.E. avec une capacités parallèles à son revenu. Les capacités au filtre obtenu viennent réalisé avec du moignon ouvert tandis que les U.E. sont vrais venu avec tous des dispositifs de la ligne de la longueur l/4 à la fréquence du travail donc que le filtre sont de type de commensurato.
16bis) J'emploie des lignes couplées dans les filtres de commensurati :
Laissant de lui le filtre passe-bas de Butterworth, les extensions à une configuration seulement constituée à partir des éléments unitaires de Kuroda ayant dedans échappent à une série d'inductance, un tel bloc peut être remplacé avec des lignes couplées les marque en particulier du fuoriesce de revenu à l'autre tête de la même ligne pour concourir le passage de le continu tandis que la ligne couplée est écluse en bref d'un côté et sur un ouvert de l'autre côté.
La condition de sorte que dont la substitution soient
valide sont qu'elles ont la même matrice de la transmission,
procédant donc dans la manière ![]() usuelle
usuelle  et sont obtenues avec l'eguaglianze e
et sont obtenues avec l'eguaglianze e ![]() de
notes
de
notes  d'ailleurs
d'ailleurs  est eu.
est eu.
À ce point égaler le B trouvé pour les lignes couplées
au B précédemment trouvé pour plus d'inductance d'U.E. obtient ![]() l'équation tandis qu'égaler nomme C que nous
obtenons
l'équation tandis qu'égaler nomme C que nous
obtenons ![]() l'équation donc résolvant l'équation
quadratique
l'équation donc résolvant l'équation
quadratique ![]() obtenons
obtenons ![]() e
e ![]() qui concourent la planification du filtre.
qui concourent la planification du filtre.
