Synthèse des filets passifs
1) conduire-point de rigidité d'un filet et fonctions d'énergie :
Les équations de Kirchoff aux noeuds peuvent être
écrites dans la forme de matriciale 
où l'i(t) il
est le porteur des courants et à lui est la matrice d'incidence qui a
transposé le relaziona également le porteur que le v(t) des tensions
cuivre avec le porteur vn(t) des
tensions 
aux noeuds par ces relations c'est atteint
l'expression 
de la puissance où b le circuit est le
nombre de constituant cuivre, transformé de Laplace est 
de quel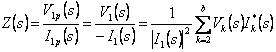 
cela dans le cas des
réécritures du filet un LC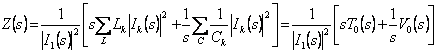 
étant T0(s) e V(s)fonctions 0 d'énergie qui elles sont toujours
vraies et non négatives.
2) propriété de conduire-point des fonctions LC :
Les zéros sont trouvés sur l'axe jW en fait plaçant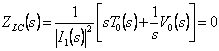 
le trova 
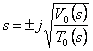qui est imaginaire dans combien les fonctions de l'énergie 0T 0 etde V coûtent vraies
et positives. Raisonnant sur l'accès de fonction un résultat
analogue pour ses zéros est trouvé et donc des poteaux et des zéros
de trouvaille de conduire-point de l'immettenze LC sur l'axe
imaginaire, ils d'ailleurs sont simples et ils sont en fait état
stationnaire imposant alterné de sinusoidale s = 0 obtient 
qui est la rigidité
qu'il devient imaginaire pur et c'est ledit reattanza et son dérivé
est 
e donc X(w) est
augmentation monotone cette il est possible choisissent si les poteaux
et les zéros sont simples et ils sont alternés. Il est eu
d'ailleurs que le comportement dans l'origine ou à infini est
celui-là d'un poteau ou d'un zéro qui implique que numerating et le
dénominateur doit différer pour 1 degré. Basé sur les
reasonings précédents peut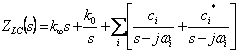 
être écrit où le c doit vrai et être le positi à vous.
3) synthèse de conduire-point des fonctions LC :
) méthodes d'adoptif
Si nous devons synthétiser une assez 
rigidité de fonction pour mettre en série une inductance 
de valeur, un condensateur 
de
valeur et de quelques parallèles des inductances 
de
la valeur et des condensateurs 
de valeur avec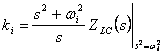 
.
Si nous devons à la place synthétiser un assez 
accès de fonction pour mettre en parallèle l'inductance
de valeur un 
, un condensateur de ¥ de
la valeurK et quelques séries
d'inductances
de valeur et de condensateurs de
valeur .
Les méthodes d'adoptif sont des réalisations canoniques dans combien d'utilisation le nombre possible minimal d'éléments.
b) Forme de Cauer
Ils sont deux bases de méthodes à vous dessus que j'emploie des fractions continues et sur le fait que le rimuovendo d'une fonction LC-RÉALISABLE un poteau dans l'origine ou un poteau au distillateur infini obtient une fonction LC-RÉALISABLE
) déplacement b1 des poteaux à l'infini
Si ZLC(s) a
un poteau à l'infini le circuit de réalisation a une inductance en
série 
de valeur, rimuovendo ce une fonction des
restes de poteau ZLC avec un
poteau dans l'origine que 1 = 1/ Z LC ayant correspondun Y
un poteau à l'infini à qui peut être enlevé et à ce qui un
condensateur parallèlement à la valeur correspond 
,
est le cos¬ continu jusqu'à ce que n'ait pas été réalisé toute la
fonction Z3(s).
) déplacement b2 des poteaux dans l'origine
Si ZLC(s) a un poteau dans l'origine que le circuit de réalisation a un condensateur dans la série 1/a de valeur, il est enlevé et c'est R-come.sopra continu.
4) Polonais des fonctions de transfert :
Pour un filet LC les poteaux de la fonction de transfert
sont simples et ils sont trouvés sur l'axe jW, parce que les filets RC et RL ils
sont simples et ils trouvent sur non simple le vrai négatif d'axe
tandis que pour les filets RLC ils sont ovunque et aussi. Tous
les poteaux des fonctions que le conduire-point ne sont pas présent
dans les fonctions de transfert, ces non actuels sont lesdits poteaux
privés tandis que tous les poteaux sur l'axe jW de la fonction de transfert doivent être présents
dans le conduire-point de fonctions dans combien doit vérifier la
condition sur le résiduel 
où l'ijde k il est le résiduel d'ijde z(s) dans le poteau s = jWi .
Les poteaux ne concernant pas l'axe jW ne peuvent pas également être présents dans le conduire-point de fonctions.
5) état de Fialkow :
Chaque filet de balance du pu² d'admittances à réduire
à un filet p constitué à
partir des admittances non négatifs au moyen de transformations t â?"y "p, 
a 
,, si de lui il déduit l'état deuxième de Fialkow que
les coefficients du numérateurde 12(s) ne doivent pas être refusé à vous et plus petit
concernant vous respectez 22 coefficients à vousde y11 (s) etde y(s), suit une partie sur laquelle nous elles ne
peuvent pas être des zéros le positif d'axe d'axe.
6) fonctions d'adimensional de transfert :
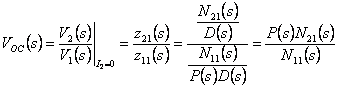
là où P(s) contient les poteaux privés du
conduire-point de fonction et 11N(s) ses zéros tandis que 21N(s) contient les
zéros de la fonction de transfert. Les coefficients du
numérateur et ceux du dénominateur sont sujets alors à l'état de
Fialkow. Des considérations analogues sont appliquées alors 
au.
7) conditionne sur la vraie partie des paramètres d'un filet passif :
de telles conditions dérivent du fait qu'un négatif de valeur de ces derniers que vous laissez vrai impliquerait l'énergie assurée à partir du filet au générateur que le filet passif n'est pas possible à un.
8) zéros des filets de balance :
Nous considérons un filet de balance constitué à partir
d'un shunt Z 1de rigidité , des séries Z 2de rigidité et d'un ij passif du filetz', la fonction de transfert est 
de ce qui démontrent que les zéros de la
transmission d'un filet de balance sont produits à partir des zéros
du shunt de stiffnesses et à partir des poteaux de la série de
stiffnesses et ils sont trouvés donc dans le semiplan gauche et sur
l'axe jW .
9) synthèse des fonctions de transfert en utilisant des filets de balance sans pertes :
Le polinomi de Hurwitz elles ont tous les coefficients
positifs vous et non nulles et les zéros sont toutes dans le semiplan
gauche, un elles propriété importante est que le rapport de la
partie égale avec la partie ou le viceversa inégale est réalisable
en tant qu'un conduire-point de l'immettenza LC. Vu une écluse
du filet LC sur un resistore les poteaux peuvent être ovunque dans le
semiplan gauche donc le dénominateur de la fonction de transfert sont
un polynôme de Hurwitz tandis que les zéros sont sur l'axe jW, ont 
de lui
dérivent qui si N(s) est égal puis 
ED 
et y22(s) est
LC-RÉALISABLE car pur si N(s) est inégal il a 
e 
y les 22 si(s) pour réaliser possède des poteaux privés
concernant yles 21(s) alors
que ceux-ci iront s'ajouter enlevé au circuit l'élément s'est
adapté pour les représenter.
10) synthèse des fonctions du transfert avec zéro décalant :
Dans le cas que les zéros de la fonction de transfert
sont ovunque de posizionati dans les croisillons symétriques sur
l'axe jW , on emploie la
technique du mouvement des zéros qui consiste en diminuant la
puissance du poteau au sottraendogli infini par 22 quantités de faire quey21 (s) ety(s) ont les mêmes zéros. Cette technique
vient utilisé afin de réaliser les approximations elliptiques de
Chebyshev-Inverso et qui exigent des zéros sur l'axe jW . Dans le pratique une limite Y 0 = Ksdoitêtre détournée à yles 22 (s) où 
.
11) filets de balance sans pertes doublement chargées :
Cette configuration au delà de comporter la cargaison 2R et la
résistance Rintérieur 1 au générateur a également la propriété
optimale de la sensibilité. Siccome le filet intérieur est LC
puis Pdedans(jw) = Pdehors(jw), en suit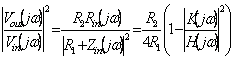 
là où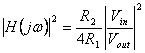 
est le capteur de
fonction et 
est le caractéristique fonctionnez.
Au moyen de suite on obtient 
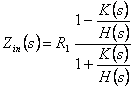l'analytics
qu'elle peut également être exprimé dans une des deux formes
suivantes :
.
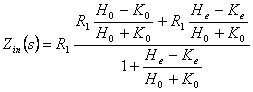
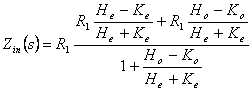12) Scalatura du trasduttore de fonction :
Il a la portée à grimper jusqu'à la sensibilité et au gain multipliant le capteur de fonction pour une constante opportune.