Introduction
1) différence entre l'analyse et la synthèse :
L'analyse consiste en étudiant la propriété des données arrange exister, elle admet donc une seule solution, la synthèse partie à la place des caractéristiques souhaitées et les extensions à une exécution possible du système donc la solution est non seulement et donc le comparazione pour l'endroit de la meilleure solution est le nécessaire.
2) évolution de realizzativa des filtres :
Au commencement les filtres étaient seulement passage utilisé à vous, la qualité des inductances sont mais pessima donc avec l'arrivée des amplificateurs opérationnels qu'ils sont venus éliminé. Actuellement elle est étirée pour éliminer également le resistori étant employé des filtres aux capacités de commutata.
3) fonction de filet :
c'est le rapport entre transformé de Laplace 
du r(t) de réponse du filet et transformé de Laplace 
de l'e(t) d'excitation.
Dans le cas le revenu est sinusoidale et le système
stable doit régime une réponse de sinusoidale avec la même
fréquence et cela qu'il reporte seulement du revenu pour le module et
la phase, parce que la fonction nette elle a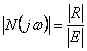 
et 
.
4) Fonctions Conduisant Le Point :
L'ébauche des fonctions définies sur la même porte, est eue :
) à conduire l'impédance de point 
b) conduite de l'accès de
point 
5) relation entre les passages d'éléments actuels dans le filtre et les poteaux à vous de sa fonction de transfert :
Pour les filets actifs les poteaux peuvent être ovunque dans le s semiplan complexe, parce que les filets RLC peuvent être dans tout le semiplan gauche ont comporté l'axe jW où mais les poteaux simples peut être trouvé simple, dans le cas des filets RC que les poteaux sont trouvés dans le semiplan gauche tandis que pour les filets LC ils sont trouvés sur l'axe jW et sont simples.
6) fonctions du transfert de la diverse typologie des filtres :
) le Passer-bas
tous les zéros sont à infini
b) le Passer-haut 
tous les zéros sont dans l'origine
c) La moitié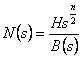 
de
de pass-band des zéros est
à la moitié infinie et autre dans l'origine
d) Le
d'entaille
tous les zéros sont sur
l'axe jW
là où dans toutes les caisses n c'est l'ordre du polynôme le B(s).
7) Denormalizzazione de la fréquence :
Si p il est le complexe et le s normalisés variables le
denormalizzata le correspondant que variable qui 
a
implique qu'un inducteur avec 
la rigidité aura la
rigidité de denormalizzata 
donc l'inducteur de
denormalizzato a 
la valeur analogue un condensateur
de denormalizzato a la valeur 
.
8) Denormalizzazione de rigidité :
Si zn(s) est la
rigidité et le z normalisésn(s) la rigidité de denormalizzata qui 
a
dans le cas d'un inducteur normalisé de L valeur implique que sa
valeur de denormalizzato est znL
tandis que pour un condensateur normalisé de la valeur C la valeur de
denormalizzato est 
.