Approximation

1) propriété de |N(jw)|² se sont associés à une fonction les rationnent N(s) :

à)       |N(jw)|² sont un rapport de polinomi égal dans le ci² de W sont obtenus remplaçant jW = s et en employant

b)       remplaçant dedans |N(jw)|² obtient où N(-s) a les mêmes poteaux de N(s) reflété mais de considérer l'origine, d'elle qu'elle dérive que les poteaux de T(s2) ont la symétrie quadrantale qui est sont symétrique considère le vrai axe qui concernant l'axe imaginaire. Une telle symétrie quadrantale est possible choisissent si les poteaux et les zéros actuels sur l'axe jW sont d'ordre égal.

 

2) fonction plate de massimamente :

La fonction est une |N(jw)|² que c'est massimamente plat au ridosso d'origine, se rappelant cela |N(jw)|² sont un rapport de l'égale de polinomi et confrontant la dernière limite obtenue au moyen de rapport avec l'expansion en série d'imper Laurin que pour être l'appartement de massimamente doit avoir le nombre plus grand de dérivés nuls dans l'origine, de lui il dérive cela |N(jw)|l'appartement ^{de 2} massimamente peut être obtenu si au = b pour le nombre plus grand possible de coefficients.

 

3) fonction de Butterworth :

On lui propose à nous de réaliser un |N(jw)|le massimamente ² plat donc à = b_{le I} , du passer-bas type donc tous les zéros de transmission sont à infini et donc tout le b sont zéro comme pur donc sauf qu'un du degré maximum, sont eus :

où au dénominateur il y a de W²ⁿ dans combien |N(jw)|² doivent être un rapport de l'égale de polinomi. La position des poteaux est qui remplace jW= s W ²=- s obtenu² po |N(jw)|² , sont eus , en particulier :

) pour n inégal avec k = 1, 3, 5, 4n-1

b) pour le pari de n avec k = 0, 2, 4, 4n-2

seulement les poteaux qui sont trouvés dans le semiplan gauche sont stables, ils sont avec e .

 

4) Polynomial di Butterworth :

C'est le polynôme qu'on trouve le dénominateur de la fonction de Butterworth où_{à 0} = 1 puisque tous les poteaux trouvent sur le cercle unitaire et d'autres coefficients sont ricorsivamente gagné au moyen d' et sont symétriques que soit_{à 0} =_{à n},_{à 1} =_{à n-1} … .

 

5) détermination de l'ordre d'une fonction de Butterworth :

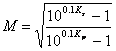L'ordre_NOTA: d'une fonction de Butterworth est où ED étant dans les listes détaillées que la bande de dépassement doit être comportée entre 0 et W_p et présenter la ligne de manoeuvre maximum du DBde K _p concernant la valeur maximum tandis que la bande d'arrêt il est comportée entre W_s et ¥ et présente une atténuation minimale de DBde K _s.

6) Denormalizzazione de la fréquence :

La fonction de Butterworth normalisé visionne une fréquence de coupe à 1 rad/sec pour lequel K_p est 3dB, pour avoir une diverse atténuation à la même fréquence, la pulsation est nécessaire pour effectuer le denormalizzazione de la fréquence étant à ce que la fonction a l'atténuation souhaitée _pde K .

 

7) Polinomi di Chebyshev :

là où le polinomi de I C_n(w) est défini au moyen d'un de suivre :

)       commençant de C₁(w) = W

b)      

c)      

d)      

ils sont tels que le module est juste-ondulation en passant la bande et diminuer monotonique dans la bande foncée. Les pulsations W qu'une atténuation de â?"3dB correspond à la pulsation de 1rad/s sont données de la relation .

Les poteaux sont remplacement gagné dedans |N(jw)|² , ils sont situent sur une ellipse à vous ont centré dans l'origine.

 

8) détermination de l'ordre d'une fonction de Chebyshev :

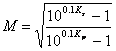L'ordre n_C d'une fonction de Chebyshev est où ED étant dans les listes détaillées que la bande de dépassement doit être comportée entre 0 et W_p et présenter la ligne de manoeuvre maximum du DBde K _p concernant la valeur maximum tandis que la bande d'arrêt il est comportée entre W_s et ¥ et présente une atténuation minimale de DBde K _s.

9) fonction de Chebyshev inverse :

il présente une juste-ondulation caractéristique en diminuant la bande foncée et monotonique dans la bande de dépassement.

Il est obtenu remplaçant W avec 1W dans qui est juste-ondulation loin partie de la passer-haute origine mais. Les poteaux qui s'en avèrent sont mutuels concernant des ces trouvaille à vous pour .

10) détermination de l'ordre de la fonction de Chebyshev inverse :

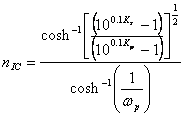
confrontant cette expression avec celle-là trouvée pour le filtre de Chebyshev on l'a qu'ils sont égale à condition qu'est eu

 

11) filtres elliptiques :

Ils sont également des filtres d'énonciations d'juste-ondulation Cauer et présentent une caractéristique est dans la bande foncée qui en passant la bande d'ailleurs est caractérise d'une plus grande pente à vous dans la correspondance de la fréquence de la coupe concernant l'autre typologie des filtres. La forme typique d'un filtre elliptique est où .

 

12) transformation de passer-haut passer-bas :

Si une passer-basse fonction est définie dans le plan complexe s = s jW au moyen de la transformation obtient une passer-haute fonction dans le plan jv de p = de u, état stationnaire de sinusoidale imposant s = 0 qu'il est obtenu u = 0 . L'effet sur la fonction du filet de N(s) est que les zéros de la transmission à l'infini venu transforment à vous dans les zéros dans l'origine. La transformation peut également être appliquée directement aux éléments d'un filet, cosicchè que un inducteur d'Henry de K transforme dans un condensateur de farad tandis qu'un condensateur de farad de K transforme dans un inducteur d'Henry.

 

13) transformation de passer-bas au pass-band :

Si une passer-basse fonction est définie dans le plan complexe s = s jW au moyen de la transformation obtient un pass-band de fonction dans le plan jv de p = de u, état stationnaire de sinusoidale imposant s = 0 qu'il est obtenu u = 0 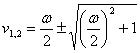. En particulier la bande de la passer-basse devient la bande du pass-band et de chaque croisillon (v₁,v2) est tel que v₁v₂= 1. Le pu² de transformation également à appliquer directement aux éléments d'une mise nette en série à chaque inducteur des capacités d'Henry un de K au farad et en parallèle à chaque capacités au farad de K un inducteur d'Henry.

 

14) réalisation d'un pass-band de filtre de type à bande large :

C'est un pass-band de filtre avec une plus grande largeur de bande concernant le filtre normalisé, le denormalizzazione dans la fréquence est obtenu alors actionnant un sur le passer-bas filtre et exécutant le passer-bas pass-band® de transformation.

15) réalisation d'une éliminer-bande de filtre :

Il est nécessaire d'appliquer la transformation à un passer-haut filtre

 

16) approximation de bande serrée :

Un pass-band de filtre serait pour se réunir fortement si sa largeur de bande est plus petite de la dixième concernant la fréquence centrale par bande qui est si . Le dénominateur du bidon de pass-band de fonction lui-même directement soit obtenu en forme de fattorizzata en fait remplaçant le nella obtient où s il est le variable considérant que le passer-bas est défini tandis que p il est le variable considérant que le pass-band est défini.