Approximation des fonctions
1) algorithme d'approximation :
) choix de la fonction rapprochante et de la norme
b) Vérification de l'existence de la solution
c) Vérification de l'unité de la solution
d) Examen des caractéristiques et la propriété de la solution
et) calcul de la solution
2) l'erreur a pesé entre une fonction pour rapprocher et rapprocher son :
étant S(y) la fonction à rapprocher, F(f,y) rapprochant et W(y) le poids de fonction qui concourt dans certains cas pour obtenir l'optimal employant également une norme différente de celle-là ce reputa nécessaire.
3) p-esima de norme :
¥ de £ du £ p du escroc 1
dans le cas de p = 1 pour diminuer la norme il correspond pour rendre le minim le secteur a comporté entre les deux fonctions tandis que pour le ¥®de p qu' il signifie pour diminuer les ordures maximum en valeur absolue entre les deux fonctions, dans ce dernier cas est parlé au sujet de la norme de Chebyshev qui peut être obtenue avec l'iterati de méthodes à vous dans un n° remarquable des étapes. La norme plus confortable est eue pour p = 2 dans combien coûte toujours possible le calcul de rapprocher dans la forme l'écluse.
4) approximation dans la norme de Chebyshev :
On lui parle au sujet du minimax d'approximation dans combien est proposé à nous pour rendre le minimum les ordures maximum entre la fonction approximative et la fonction rapprochant au moyen d'opportun choisi des coefficients d'un polynôme ou une fonction les rationne qu'elles constituent rapprocher polynôme.
5) meilleur rapprocher dans la norme de Chebyshev :
L'état nécessaire et suffisant de sorte que F(f,y)
fonction continue en I) soitmeilleurrapprocher que… S(y) (est que l'erreur 
de courbe a au moins des alternances de n dans le ce est est n 1
points dans qui 
étant n le n° des membres du
porteur f.
Si j il appartient à
avec le format discret de n 1 il vise la meilleure approximation est
obtenu résolvant le système linéaire 
si à la
place j il appartient à avec le
format discret de plus que n 1 points qu'il est nécessaire de
caractériser avec l'estremale composé de n 1 points sur lesquels la
meilleure approximation correspond à la meilleure approximation
dessus à du départ.
6) minimax polynôme d'approximation :
Le polynôme 
qui part peu d'une fonction
continue assignée est un univocamente déterminé dans combien le n°
des points consécutifs dans la correspondance du que le â?"S(de Pn
(y)y) assume avec alterné signe
la valeur maximum n'est pas plus petit de n 2, il la vérification qui
est les relations 
e
.
Être célèbre avec l'estremale il ne peut pas être calculé avec l'iterati de méthodes à vous au moyen de l'algorithme de Remel ou de Stiefel.
7) algorithme de Remel :
) à donné une fonction à
S(approximatify) et le polynôme
rapprochant des points de les mêmes sont n choisi 2
et les équations sont écrites , cela qu'il peut
résoudre concernant le n 2 incognitoà j caractérisant d'une telle manière rapprocher polynôme
b) Pour chaque point y la fonction est erreur estimée, si remplacement il au moins des temps de n 1 et n'assume pas de plus grandes valeurs absolues de |Et| l'optimal a été attrapé vers le haut d'autrement est nécessaire pour changer avec des points choisit à vous comprenant les points présentez l'erreur avec dont une plus grande valeur absolue |Et| choisi toujours avec le critère de l'alternance de l'erreur entre les points consécutifs.
8) algorithme de Stiefel :
) à donné le S(functiony) assigné au moyen d'un nombre fini de points, s'ils choisissent un certain n 2 afin de former un polynôme de l'ordre n
b) les montants sont estimés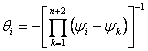 
avec 1 = 1, 2 … , n 2
c) est estimé la ligne de
manoeuvre maximum 
d) on l'estime pour le polynôme d'interpolation le Pn(y) en utilisant le premier et dernier n 1 points de l'intégralité {y}
et) l'erreur dans la correspondance de tous les points est estimée de avec prechosen et le point est correspondant choisi à l'intégralité plus élevée, un tel point vient remplacé à ce plus étroitement dans ce que l'erreur du même signe est eue
f) péché d'itera quand l'erreur optimale n'est pas obtenue.
9) le minimax d'approximation au moyen de fonctions les rationne :
On emploie encore l'algorithme de Remes que le per², étant rapprochant elles rationne, donne l'endroit à un système non linéaire qui peut être résolu dans une des manières suivantes :
) en utilisant des artifices afin d'éliminer la non-linéarité
Le système vient récrit dans la forme 
où 
célèbre si est simplement un poids
de fonction, en particulier est procédé pendant qu'il suit :
a1) qu'ils fixent arbitrairement des coefficients les
commence pour B(y) et le
correspondant se résout problème de minimax pesé d'approximation 
a2) il procède lui-même résolvant à l'étape
générique n le minimax de
problème 
a3) si le procédé converge à une étape générique L ha BL-1(y) @ BL(y)
b) Résolution du système non linéaire
b1) dans les méthodes directes la quantité est célèbre provisoire assumé et
) méthodes b2 indirectes
