Éléments de mécanique de quantistica
1) équations de Hamilton - Jacobi :
ils sont des équations en position à décrire complètement l'évolution temporelle d'un système duquel le hamiltoniana est célèbre.
2) comparaison entre les vagues et les classiques de particules de systèmes :
La position, les vitesses et l'énergie d'une particule
classique peuvent être définies avec la précision infinie alors que
pour 
une vague si x sont célèbres le k ne sont pas
célèbres et le viceversa.
3) causes de la crise de la mécanique classique :
Les effets suivants ne trouvent pas l'explication avec la mécanique classique :
Fantôme de l'émission du corps noir
La théorie classique de Rayleigh et de jeans a déterminé que pour l0® l'énergie émise du corps noir étire à infini, alors que dans la vérité les expériences les étire à 0, que l'hypothèse de Planck est que l'échange de l'énergie entre les murs du corps noir et l'annulation se produit dans le multiple de forme de quantizzata de l'combien et0= hn .
Effet photoélectrique
On a l'ébauche de l'émission d'électron de la partie investie de pleine d'un paquet léger, expérimentalement qui si la fréquence de l'incident de photon est plus petite d'un minimum pas il n'extrait indépendamment aucun électron à partir des incidents de nombre de photon alors que si la fréquence est assez plus grande également un photon simple afin d'extraire un électron et le nombre est proporziona ils au nombre d'incidents de photons. L'explication est venue fourni à partir d'Einstein qu'elle a supposé que l'onde électromagnétique rapporte aux électrons l'énergie dans les multiples de combien de élémentaire etde 0= hn .
Modèle atomique de Bohr
Le fantôme de l'émission d'un atome s'avère caractérisé des lignes très distinguées, la raison de celle a été trouvée dans le modèle de Bohr qu'elle visionne préalablement que les électrons mettent en boîte le ruotare autour au noyau seulement sur des orbites stationnaires très définies de la quantification du moment angulaire et que sur de telles orbites les électrons n'émettent pas l'annulation.
4) longueur d'onde de De Broglie :
relation importante en combien alliage coûte une une taille au corpuscolare à une taille d'ondulatoria.
5) équation de Schroedinger :
6) principe de correspondance :
7) équation de continuité :
8) produit à l'élever des fonctions de vague :
9) valeur prévue de observable :
dans le cas du hermitiani de fonctionnement on l'a que la valeur prévue est une vraie taille.
10) solution de l'équation de Schroedinger dans le cas des mises à niveau elles indépendantes du temps :
Il est possible de décomposer des mises à niveau elles
dans le produit f(r,t) = l'u(r)
de T(t) que pour l'employé de pièce du temps il a 
la solution tandis que l'employé de pièce du temps de
l'endroit à l'équation à l'autovalori 
que la
solution générale a 
.
11) principe de l'indétermination :
c'est un principe qui dérive pas du commutatività entre la position de fonctionnement et l'élan de fonctionnement.
12) fonction de la vague de la particule libre :
L'ébauche d'une vague plate 
et de
l'électron a l'élan 
.
13) fonction de la vague de la particule dans un trou des mises à niveau elles aux murs infinis :
L'assumer les améliore nuls entre le â?"a et à et ¥ à l'extérieur, on l'a que les
niveaux de l'énergie accordée supposent que 
les
valeurs et la fonction de la vague pour n inégal vaut la peine 
tandis que pour n l'égale vaut la peine 
.
14) fonction de la vague de la particule dans un trou des mises à niveau elles aux fonds :
L'assumer les améliore nuls entre le â?"a et à et U0 à l'extérieur, un constate que
le fils énergique de niveaux ceux qui satisfont les équations
importantes
pour les solutions égales et 
pour les solutions inégales étant 
et 
.
15) quantizzate d'énergies dans le cas d'un oscillateur harmonique :
Les niveaux énergiques permis sont 
ont
donc une énergie minimale non nulle pour n = 0 et les niveaux de
quantici sont distance à vous entre ils des multiples de 
.
16) probabilité du perçage d'un tunnel :
La probabilité du perçage d'un tunnel diminue
l'esponenzialmente à l'augmentation du larghezza d de la barrière
qui est 
.
17) densité des états dans les caisses tridimensionnelles, bi-dimensionnelle, monodimensional :
Dans le cas de la particule libre 3D 
est
eu, pour la particule dans un trou des mises à niveau elles aux murs
infinis qui est 2D libre a 
tandis que pour le fil de
quantico qui est le 1D libre de particules est eu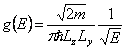 
18) fonction de distribution pour la particule classique, fermion, bosone :
Le f(E) de fonction de distribution représente la
probabilité que l'état à l'énergie et a de l'occupation, parce que
une particule classique a la distribution de
Maxwell-Maxwell-Boltzmann 
, parce que les fermions il
caractérise à vous du semintero de rotation a à la place la
distribution de Fermi-Dirac 
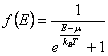et finalement pour le
bosoni ayant la rotation entière la fonction de la distribution de
Bose-Einstein est eue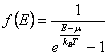 
.