Le Z Transformé
1) Z bilatéral transformé :
c'est une prolongation de transformée de Fourier, cela qu'elle est évidente si le complexe variable z dans la forme polaire est placé :
on l'observe en fait que les fonctions aiment l'étape que pour par l'intermédiaire de de sa discontinuité il n'admet pas transformé de Fourier, peuvent être modifiées du r exponentiel- n .
2) Critère de la convergence des ordres à la longueur finie :
Ils convergent ovunque pour 0 < |z| < le ¥ , la valeur de ¥ ne peut pas être assumé si la fin inférieure de la récapitulative est négative alors que la valeur 0 ne peut pas être assumée si la fin avançée de la récapitulative est positive.
3) Critère de la convergence des ordres au monolatere habile :
Ils convergent à l'extérieur d'un cercle du faisceau Xde R .
4) le Critère de la convergence des ordres au monolatere est parti :
Ils convergent à l'extérieur d'un cercle du faisceau Xde R .
5) Antitrasformata Zeta :
là où C est une distance arbitraire fermée située dans la région de la convergence de X(z) et cela il encercle l'origine.
En bref 3 des méthodes distinguées peuvent être employées afin de déterminer antitransformed z d'un l'ordre :
) = additionnez le résiduel de X(z)zn-1 dans les poteaux intérieurs
à C où le résiduel d'un poteau k d'ordre est calculable par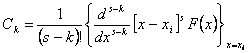 
.
b) désirent ardemment la division qui concourt pour caractériser un ordre dont est nécessaire mais pour le savoir pour écrire une écluse de forme.
c) La décomposition dans le fratti simple, en bref doit être effectuée une division avant si le degré du numérateur est plus grand du degré du dénominateur, va décomposé dans un produit des monômes, qui seront chacun le dénominateur de fratti de la somme de n simple.
6) les régions de la convergence de transformée zéta les rationnent :
Habile un ordre de monolatera converge à l'extérieur du cerchio a ;
un ordre gauche de monolatera converge à l'intérieur du cerchio a ;
un ordre bilatéral converge à l'extérieur d'un anneau circulaire.
7) propriété du Z transformé :
 |
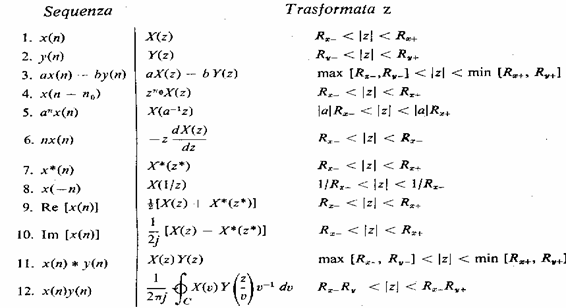8) relation entre la fonction du transfert et la réponse dans la fréquence :
elles coïncident seulement sur le cercle unitaire.
9) relation entre un système stable et la région de convergence :
On l'a qu'un système est stable si la région de la convergence de la fonction de transfert comporte le cercle unitaire.