Techniques du plan des filtres numériques
1) algorithme pour le plan des filtres numériques :
) le détail de la propriété a exigé pour le système
b) Approximation des listes détaillées pour des moyens d'un système au temps discret
c) Réalisation du système en utilisant l'arithmétique à la précision finie
2) méthode pour la planification des filtres IIR :
Un filtre analogique est transformé dans le détail que un filtre numérique satisfaisant a déterminé ceci parce que les méthodes de plan des filtres analogiques sont des formules beaucoup valides et d'utilisation dans l'écluse simple de forme et.
3) Invarianza à l'impulsion :
En bref qu'autre n'est pas fait à cela pour capturer un
nombre sûr de champions de la réponse à l'impulsion du filtre
analogique, la relation est eu 
. On l'observe
que l'axe imaginaire dans la carte du plan s sur la circonférence
unitaire tandis que la moitié gauche de chaque bande actuelle dans la
carte de s sur la partie intérieure de la circonférence unitaire
tandis que demi de carte habile sur la partie externe de la même.
Étant basé sur le prélèvement cette méthode il peut
présenter le crénelage et donc son j'emploie est concentré sur les
limites de systèmes à vous dans la bande.
On l'observe que si les poteaux dans s sont stables que soit à la vraie partie négative les poteaux du filtre numérique sont contenus à l'intérieur du cercle unitaire dans Z donc aussi l'alerte numérique de filtre à être stable.
4) transformation bilinéaire :
Le Z transformé de la réponse à l'impulsion du filtre
numérique peut être simplement remplacement obtenu 
dans le T.d.L. de la réponse à l'impulsion du filtre
analogique. La transformation bilinéaire est donc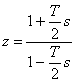 
et trace l'axe imaginaire du plan s sur la circonférence
unitaire, envoie la gauche semiplan dans s à l'intérieur du cercle
unitaire et envoie la gauche semiplan à l'extérieur de le même.
Avec cette transformation que un filtre numérique est
commencement obtenu d'écurie stable par filtre analogique, d'ailleurs
n'est pas le crénelage eu mais la déformation de phase est eue.
5) filtres numériques Butterworth :
Un filtre de Butterworth est caractérisé d'une réponse
dans l'amplitude plate en passant la bande, 
où N
est l'ordre du filtre et combien plus coûte grand beaucoup plus de
réponse du filtre est approché la réponse du filtre idéal tandis
que Wc est la
pulsation analogique de la coupe pour laquelle le module est réduit
à 0.707 de la sa valeur maximum.
On l'observe que sont l'equidistanziati des poteaux 2N sur une circonférence du faisceau Wc dans le plan s et sont arrangés symmetricalally concernant l'axe imaginaire de ces poteaux sont stable seulement ceux qui tombent dans la gauche semiplan.
Si un filtre numérique est projeté pour partir du filtre analogique de Butterworth qu'il obtient une circonférence centrée dans l'origine alors que la circonférence de Butterworth il n'est pas, d'ailleurs les poteaux ne sont pas davantage equispaziati dans le ci² court qu'il fait doit déterminer les poteaux stables du filtre de Butterworth et de mapparli par la transformation bilinéaire sur le cercle unitaire.
6) filtres numériques Chebyshev :
L'ébauche d'avoir l'oscillation uniforme de filtres dans
la bande passant et monotone dans la bande foncée ou monotone dans
l'oscillation foncée de bande et d'uniforme en passant la bande, a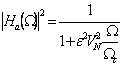 
où 
est le polynôme de Chebyshev
pour lequel la formule de la répétition est définie 
tandis qu' et est
admise que la fonction de l'ondulation en passant la bande et le Wc est la
pulsation souhaitée de la coupe. Les poteaux de ce filtre sont
disposés sur une ellipse dans le S plat.
7) filtres elliptiques :
L'ébauche des filtres qui concourent d'avoir une atténuation uniforme est dans la bande de dépassement qui dans la bande foncée, il est eue
étant UN(w) une fonction elliptique de Jacobi.
Afin de réaliser ce type de filtres qu'ils sont nécessaires
est des poteaux que des zéros et derniers sont disposé sur l'axe JW du S plat.
8) réalisation des filtres passer-hauts, du pass-band et de la éliminer-bande :
Avant qu'un passer-bas filtre à la fréquence
normalisée avec une soit projeté des méthodes précédentes et
alors au moyen de transformations d'algebriche la caractéristique
souhaitée est obtenue, est en particulier la variable associée z à
la fonction du passer-bas transfert et le Z variable à la fonction
souhaitée du transfert, entre ils vige
la
transformation à partir dont pour des valeurs opportunes de N et à k la
transformation souhaitée est obtenue.
9) le plan des filtres numériques IIR a aidé au calcul :
Puisque les procédures analytiques n'existent pas nous pour le plan des filtres analogiques ou numériques qui satisfont les listes détaillées arbitraires, elles ont été techniques affirmé de la planification soluble au caractère général mais seulement au calcul.
) Minimizzazone de l'erreur quadratique moyenne
La réponse dans la fréquence souhaitée doit
être assignée pour un n° discret des fréquences, dans la
correspondance di.le qui est définie le milieu quadratique
d'erreur 
, admettant pour le filtre que une fonction 
de transfert est nécessaire pour déterminer les
valeurs des coefficients qui diminuent l'erreur quadratique moyenne
qu'il est possible résolvant le système des équations qui est
uguagliando obtenu à zéro le respect partiel de dérivés à chacun
des coefficients.
b) Minimizzazione de l'erreur p d'ordre
On diffère seulement de la méthode précédente
parce qu'il vient diminué pas l'erreur quadratique moyenne mais un
milieu pesé de sa puissance ou 
lui de p-esima est
travaillé sur le groupe retardent.
10) plan de SAPIN de filtres avec l'utilisation des fenêtres :
En nature la fonction souhaitée du transfert Hd(etjW) pour un filtre sélectif est
constante aux heures qu'il implique que la réponse à la
correspondance le champion unitairehd (n) est un ordre infini, dans
l'ordre pour le rendre fini et le motif peut être coupé, est donc
h(n) = h obtenusd(n)w(n) où
w(n) que c'est la fenêtre qui peut être rectangulaire, triangulaire
ou de Bartlett, Hanning, Hamming, Blackman. Étant l'ébauche 
de relation de périodique un convoluzione continu
donc combien plus transformé de Fourier de la fenêtre coûte
poignée, beaucoup moins de fantôme sera dulled concernant le
fantôme souhaité, en particulier on l'a que la fenêtre
rectangulaire est celle-là qui a le lobe principal plus de détroit
mais les lobes secondaires sont élèvent beaucoup à vous, afin de
les abaisser est nécessaire de mat la fenêtre des extrémités qui
est possible avec les autres types de fenêtres que mais présentez un
lobe principal plus au loin un et donc un plus grand smussamento.
La largeur du lobe principal est d'ailleurs proporziona
d'inversamnte ils à N.
11) le plan du SAPIN de filtres a aidé du calcul :
Ils sont pris des champions une période de la réponse dans la fréquence souhaitée après quoi elle est procédée pour l'interpolation, une plus grande atténuation dans la bande foncée mettent en boîte un ou deux mais soient obtenues prenant des champions dans la bande de transition. Avec cette méthode ils sont obtenus des filtres avec d'excellentes caractéristiques mais aux dépenses d'une plus grande complexité du plan concernant les filtres qu'elle réalise à vous avec i employez-la des fenêtres.