Estime du fantôme de puissance
1) paramètres statistiques d'un processus aléatoire stationnaire :
valor moyen
milieu temporel
milieu temporel de chaque champion d'ordre
désaccord
autocovarianza
densité spectrale de puissance
2) estime de la moyenne :
elle représente seulement une estime précise si N est un nombre élevant beaucoup.
3) bon priseur :
Il est un priseur pour lequel on élève la probabilité qui l'estime est à côté du paramètre à estimer, cela est la densité de probabilité doit fortement et être concentré autour à la valeur vraie.
4) polarisation d'un priseur :
C'est la différence entre la valeur vraie à du paramètre et la valeur prévue 
de l'estime.
5) désaccord d'un priseur :
6) erreur quadratique moyenne d'un priseur :
7) priseur de consister :
Il est un priseur pour lequel la polarisation et le désaccord étirent tous les deux à zéro à la croissance du nombre d'observations.
8) estime au verosimiglianza maximum :
Estime au verosimiglianza maximum du milieu de valor le mX d'un processus aléatoire
est la collection moyenne d'échantillons
caractérisés d'un désaccord 
et de la polarisation
nulle donc puisqu'à la croissance de N le désaccord diminue elle a
que la collection moyenne d'échantillons est un priseur de consister.
Estime au verosimiglianza maximum du désaccord d'un processus aléatoire
, au cas où mX ne serait pas célèbre peut être remplacé dans
l'expression de son estime, est le per² eu que la valeur prévue du
champion de désaccord ne coïncide pas avec le désaccord pour N
petit présentant donc une polarisation qui au scompare pour le
¥®de N . On a le désaccord
du champion de désaccord 
est donc que le champion
de désaccord est une estime consistante.
9) estime de l'ordre de l'autocorrelationship d'un processus nul à la moyenne :
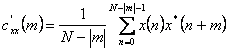
ébauche d'un priseur consistant en combien n'a pas été polarisé et ses bouts droits de désaccord à zéro pour le ¥®de N .
10) estime de l'ordre de l'autocorrelationship d'un processus nul à la moyenne :
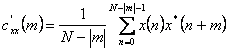
ébauche d'un priseur consistant en combien n'a pas été
polarisé et ses bouts droits de désaccord à zéro pour le ¥®de N. C'est un per² eu qui
si m®N que le désaccord de l'estime se développe
remarkablly rendant mêmes l'estime non utiles, un tel inconvénient
n'est pas à la place présent dans 
l'estime.
11) Periodogramma d'une femme blanche d'ordre :
c'est une estime polarisée du fantôme de la puissance
Pxx(w) dans combien sa valeur prévue ne coïncide pas avec
transformée de Fourier de l'autocorrelationship jxx(m), ce résultat s'obtient
considère le periodogramma comme transformé de Fourier de l'estime cxx(m) qui de l'estime làxx(m). Le désaccord
du periodogramma est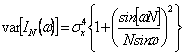 
et il ne s'étend pas à 0
pour le ¥®de N donc que
le periodogramma n'est pas une estime consistante, ont en particulier
des oscillations croissantes à la croissance de N.
12) Periodogramma d'un bruit coloré :
là où 
est le periodogramma d'un
bruit l'homme et le P blancsxx(w) est la densité spectrale de la
puissance du coloré ébruitent. Le désaccord du periodogramma
est 
, donc le periodogramma qu'il n'est pas un
priseur de consister et il présente des oscillations remarquables
autour de la valeur vraie du fantôme.
13) méthode de Bartlett pour l'estime du fantôme :
Chacun consiste en subdivisant l'ordre donné le x(n)
dans des segments de K des champions de M, est estimé le
periodogrammi de K dans
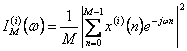la forme qu'elles est
entre le indépendant elles et donc l'estime du fantôme assume 
l'expression, sa valeur prévue est le convoluzione du
fantôme vrai Pxx(w) avec transformé de Fourier de la fonction le
correspondant rectangulaire de fenêtre à un periodogramma calculé
sur des champions de N, les bouts droits de désaccord à 0 à la
croissance du nombre de champions de N donc l'estime de Bartlett
consiste. On l'a qu'à la croissance du n° du periodogrammi le
désaccord que la résolution du fantôme diminue mais également.
14) méthode de fenêtres pour l'estime du fantôme :
Le periodogramma est considéré dulled 
après avoir attendu le varianza 
de la
valeur e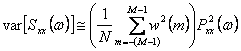 
dont on l'observe que le periodogramma
asymptotiquement il n'est pas polarisé.
15) méthode de gallois :
C'est une modification de la méthode de Bartlett, en bref
que le w(n) de fenêtre vient appliqué directement à chaque
sottosequenza des données obtenues du x(n) d'ordre de revenu,
obtiennent donc le periodogrammi de K modifié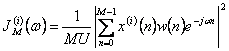 
où 
est un facteur de necessaario de la normalisation de
sorte que 
l'estime asymptotiquement ne soit pas
polarisée.
16) application du FFT aux méthodes de Bartlett ou gallois pour l'estime du fantôme du potenza :
Il est nécessaire de calculer pour chaque sottosequenza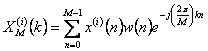 
au moyen d'un algorithme de FFT, elles sont
estimées
alors et elles additionnent un à l'autre
jusque 2'à l'i=K finalement le résultat divisé de và pour KMU.
17) application du FFT au calcul de l'estime du correlationship :
Un premier procédé est :
) l'ordre de L est construit un dirige ajouter le x(n) aux zéros (M-1)
b) le DFT est estimé sur L objectifs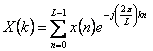 
contre k = 0.1 … , L le â "1
c) est estimé le DFT inverse sur L objectifs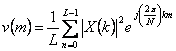 
contre m = 0.1 … , L le â "1
d) 
trompeur m =
0.1 … , â "1 de M
Selon le procédé il est à la place :
) l'ordre 
est construit et si de lui il
calcule transformé sur des points de 2M