Calcul de transformé de Fourier discret

1) formules du DFT :

pour k = 0, 1 … , N-1

pour n = 0, 1 … , N-1

 

2) propriété d'utilisé afin d'améliorer l'efficacité du calcul du DFT :

 

3) algorithme de Goertzel  :

là où

c'est un algorithme qui exige les vraies multiplications 4N et les vraies additions 4N afin de gagner X(k) pour chaque k.

Une amélioration de la complexité est obtenue au moyen de l'algorithme de Goertzel modifié basé sur la fonction 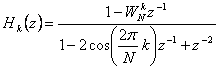du transfert.

 

4) algorithme de FFT basé sur la décimation dans le temps :

En bref que le x(n) d'ordre vient décomposé dans le sottosequenze graduellement plus petit en particulier à la première étape livre vers le haut du ciascuna de deux ordres des têtes N/2, d'un relativement aux pairs et l'autre relatif au nombre impair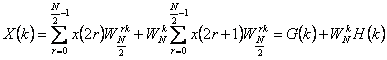

 

5) équations d'un papillon dans le temps :

 

6) algorithme de FFT basé sur la décimation dans la fréquence :

En bref que l'ordre de X(k) vient décomposé dans le sottosequenze graduellement plus petit en particulier à la première étape livre vers le haut du ciascuna de deux ordres des têtes N/2, d'un relativement aux pairs et l'autre relatif au nombre impair

 

7) équations d'un papillon dans la fréquence :

 

8) algorithme du gazouillement transformé de Z :

Il concourt pour calculer non seulement le Z transformé d'un ordre générique sur le cercle unitaire mais dans les points (… e) trompeur qui à changer de k de 0 à M-1 décrivent une spirale, transformé dans ces points vaut la peine 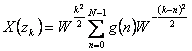qui est présente pendant qu'on peut donc penser un convoluzione de l'ordre à un filtre de gazouillement avec la réponse le champion unitaire , ébauche d'un ordre à la durée infinie donc afin de pour être estimé le FFT est le nécessaire son segmentazione.