Mécanique d'Ondulatoria

1) relation de De Broglie :

Les appuis de De Broglie que la lumière a une double nature, au particellare et à l'ondulatoria pour lesquels à un électron elle est associée est l'une masse qui une vague. La relation qui allient la longueur d'onde l de l'annulation à son élan .

 

2) observable et opération :

L'observable est la propriété mécanique qui peut être mesurée comme la position X, l'élan p et l'énergie et tandis que ceux de fonctionnements sont utilisation vous dans la mécanique de quantistica et la mécanique d'ondulatoria et dans l'ébauche courte des instructions mathématiques particulières. Observable et fonctionnant ils sont réunis d'une relation importante qu'elle affirme

que les valeurs possibles mesurables simples pour observables sont ceux pour lesquelles .

Elles sont d'importance particulière l'élan de fonctionnement et le total de fonctionnement d'énergie qui également s'appelle Hamiltoniana.

 

3) valeur moyenne d'un ordre de beaucoup de mesures de observables :

 

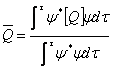
4) équation de Schroedinger :

Il décrit la fonction de la vague y(x, y, z, t) qui est la vague s'est associé à une particule dotée de massa.

.

 

5) physicien signifié de la fonction de vague :

L'image de module de la fonction y de vague qui est représente la densité de la présence de la particule dans le point X, y, z au temps t. Une telle densité disparaît multiplié pour une constante de la normalisation qui rend unitarian l'intégrale calculée sur tout l'espace.

 

6) principe de l'indétermination de Heisenberg :

Il affirme qu'il y a des croisillons conjugués de variable pour lesquels quand il augmente le degré de connaissance d'une diminue automatiquement le degré de connaissance de l'autre, le croisillon de la variable de l'intérêt pour le quantistica est l'élan et la position du puits Heisenberg d'électron affirme cette date les dimensions réduites de cette particule, quand nous au moyen d'un essai de proton à caractériser de la position que nous savons pour avoir pris elle mais les rendements de photon à l'énergie d'électron et il l'envoie à la qualité de clignotement sait d'où. Le principe de l'indétermination de Heisenberg affirme que le produit des incertitudes vaut la peine .

 

7) solution de l'équation de Schroedinger dans la caisse libre de particules :

Le temps est nécessaire pour placer V = 0 dans l'équation de Schroedinger indépendant et se limiter au cas d'unidimensionale, est obtenue :

En bref on l'a que la particule peut être ovunque, nous qui est ont une indétermination totale sur la position étant moment pour le moment complètement célèbre l'élan.

 

8)       état de Bragg :

C'est la condition pour imposer à la longueur d'onde d'un incident d'annulation avec un angle q concernant l'axe X de sorte qu'il puisse donner l'endroit à l'interférence constructive si sended contre des plans réticulaires sépare de la distance d. le condizione à vous

il est caractériser obtenu immédiatement au-dessous du plan réticulaire, concevant le faisceau qui réfléchit là-dessus et estimant la longueur optique dans plus concernant la réflexion sur le plan surplombant. De sorte que les deux faisceaux aient lieu dans la phase soient nécessaires qu'une telle différence de la distance soit un n multiple de la longueur d'onde l. Il est nécessaire d'employer une prochaine longueur d'onde à la distance entre les plans est donc nécessaire d'employer en tant que sonde des faisceaux de I X.

 

9) Calcolo di Laue pour l'amplitude de la vague diffuse et du bonnet mutuel :

L'ébauche d'un calcul qui vient a présenté afin de limiter l'erreur de la base du calcul de Bragg, celui considère les plans réticulaires comme des miroirs se reflétants parfaitement et donc.

Un des points du bonnet comme l'origine est considéré ou, un point situé à une distance r de lui vient investi d'une vague plate que nous considérerons toujours chronométrer t = 0. Dans r est eu mais ce point devient source des vagues sphériques secondaires pour lesquelles l'amplitude de l'annulation sur l'endroit de détecteur à une distance r de r et R de l'origine il est où le Kr ils sont les modules parce que dans une vague sphérique les deux porteurs sont toujours des parallèles.

L'image de module de l'amplitude de l'annulation trouvée est le maximum dont elle est obtenue décommandant le dénominateur pour lequel est et donc où q il est entier.

Les conditions de Laue pour la diffraction maximum sont obtenus donc :

là où q, r, s est des nombres entiers ils sont à la base de la définition du bonnet mutuel dans combien les porteurs de la traduction du stesso

ils sont tels qu'un celui qui ils combinaison linéaire satisfait les équations de Laue pour la diffraction maximum.