Rappels de service sur la marque ils

ELLE MARQUE LES DÉTERMINE À VOUS DANS LE DOMINION DU TEMPS

1) énergie des marques elles :

L'énergie est l'intégrale de la puissance instantanée , si elle suppose que les marques finies d'une valeur alors est dite elles à être d'énergie.

 

2) puissance moyenne des marques elles :

Dans le cas elle les marque que le s(t) est sans limites dans le temps et il n'a pas fini l'énergie, leur considère la puissance moyenne temporelle des marques les marques d'essendo les ont coupées. Si pour des données il les marque il assume une valeur finie, alors des marques est dit elles à être de puissance.

 

3) Valor moyen des marques elles :

, il est divers des solos 0 pour des marques elles de la puissance.

 

4) le membre les a alternées des marques s(t) :

 

5) facteur de crête :

On lui rapporte aux marques elles symétriques, qui manquent dans le membre continu et ont l'égale et vis-à-visde la valeur maximum s _M etde la valeur minimale s _m |s_m| = s_M = s_p , est eu :

 

6) fonction de cornue :

dans pratique elle les marque que la cornue est s'ajouter obtenu les marque qu'elles obtiennent le traslando les marque x(t) d'une quantité multiple de la période T₀ de la répétition, est observées qui seulement si la période T₀ est plus grande de la période T_X d'elle les marque la source obtient un cours semblable à elle.

 

7) puissance des marques elles périodique obtenu pour la répétition des marques les de la durée finie :

étant E(T₀) l'énergie calculée à l'intérieur d'une période, elle coïncide avec et seulement si T_X < T₀ .

 

8) fonction d'intercorrelationship temporel ou de corrélation mutuelle temporelle pour des marques elles de l'énergie :

caractérise le degré de similarité entre 2 le funzioni, attention au fait qui ne coïncide pas avec le produit de convoluzione.

 

9) énergie mutuelle :

L'ébauche de la fonction de l'intercorrelationship a calculé dans t = 0 .

 

10) le produit à l'élever de 2 les marque de l'énergie :

L'ébauche de la valeur dans l'origine de la fonction de l'intercorrelationship entre deux les marque , mesurent l'affinité du traslati de deux marks pas ils.

 

11) il les marque des parallèles, antipodali, orthogonal :

La devise l'index de l'intercorrelationship est eue :

) ž_xy de r = 1 elle les marque des parallèles

b) ž_xy de r les = 0 les marquent orthogonaux

c) le ž-1 _xy de r = les marque antipodali

 

12) fonction de l'intercorrelationship des marques elles de la puissance :

 

13) fonction de covarianza temporel pour des marques elles de la puissance :

C'est la fonction de l'intercorrelationship temporel des membres à la nulle de milieu de valor :

 

14) la relation entre l'intercorrelationship et l'intercovarianza de deux les marque de la puissance :

 

15) famille d'incorrelati de marques ils :

Une famille des marques elles indique l'incorrelata si toutes les fonctions du covarianza K(t)_xy est nulle.

 

16) famille des marques elles incohérentes :

Elle est avec des marques elles de la puissance pour laquelle pour chaque t les fonctions de l'intercorrelationship R sont nulles tous(t)_xy, parole également cette ébauche d'une famille des marques elles orthogonales.

ELLE MARQUE LES DÉTERMINE À VOUS DANS LE DOMINION DE LA FRÉQUENCE

17) transformé de Fourier :

là où S(f) est le fantôme des marques elles, en particulier dans le cas que le s(t) est des marques elles vraies, le fantôme d'amplitude est une fonction égale tandis que le fantôme de phase est une fonction inégale.

 

18) Antitrasformata di Fourier :

c'est lui les marque que le s(t) est esprimibile au moyen de la somme d'un nombre infiniment des fonctions et ^{du j} harmoniquescomplexes^Wt de l'amplitude infinitésimale et de fréquence f distribuée de la manière continue sur le vrai axe.

 

19) propriété de transformée de Fourier :

 

20) F [ 1 ] :

d(f)

 

21) F [ sgn(t) ] :

 

22) F [ u(t) ] :

 

23) F [ rect(t/T) ] :

 

24) F [ sinc(t/T) ] :

 

25) série de Fourier des marques elles temps continu périodique :

être C_n avoir des coefficients d'expression 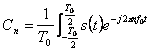de Fourier, appliquant transformé de Fourier obtient qui est a un fantôme discret et toutes les lignes sont espacées d'une quantité .

 

26) densité spectrale d'énergie :

à partir d'elle l'énergie peut être obtenue des marques les intégrant sur l'axe des fréquences.

 

27) densité spectrale de puissance :

Elle est transformée de Fourier de la fonction de l'autocorrelationship pour des marques elles de la puissance, celle est :

 

28) il les marque limité dans la bande étroitement :

Le fantôme de l'énergie d'E(f) est une vraie fonction égale pour des marques elles vraies dans le cas idéal, se prolonge entre la fréquence maximum f_M et une fréquence minimale f_m , la bande des marques elles est donc B = f_M - f_m , définition valide également dans le vrai cas où le fantôme est sans limites mais peut négliger les fréquences au-dessus de f_M et sous f_m .

 

29) il les marque dans la base de bande :

C'est les marks un typiques les a fournis à partir d'un émetteur d'informations, sa bande est donc allocata 0 £ f_M du £ f_m, l'axe positif simple d'axe est considéré parce que pour la vraie et égale fonction les marque vrais le fantôme d'énergie est un.

30) il les marque dans la bande de traslata :

Il est élaboration obtenue les marque dans la base de bande au but pour l'adapter aux moyens de trasmissivo, sa bande est donc allocata :

0 < £f _M du £f _c de f_m

beaucoup souvent la prolongation de la bande est approximativement égale à la fréquence maximum f_M , bien que la fréquence minimale f_m soit diverse de zéro.

 

31) il les marque dans la bande serrée de traslata :

C'est des marques ils qu'il respecte la condition ou le B < le f_m .

 

32) il les marque dans la bande de traslata beaucoup de poignée :

C'est des marques ils qu'il respecte la condition où f_c est une fréquence contenue à l'intérieur de la bande de B, cette condition inclut .

RAPPRESENTAZIONI ULTÉRIEUR DE MARQUE ELLES

33) fantôme des marques elles de la vraie énergie :

L'ébauche d'une fonction égale, est donc suffisante pour étudier le fantôme qui se prolonge dans l'axe d'axe négatif ou le fantôme qui se prolonge dans l'axe positif d'axe .

 

34) il les marque analytiques :

Pour les linéarités du antitransformed un de Fourier on l'a que qu' au fantôme correspond du reste de marques elles vraies est le hermitiano donc qui correspond remplaçant a être les marque associé analytique au s(t). Dans la vérité la forme complète des marques elles analytiques est où sont transformées de Hilbert de s(t).

35) transformé de Hilbert de s(t) :

est transformé de Hilbert de s(t), que de lui le s(t) de riottiene au moyen d'antitransformed un

. Dans le dominion de la fréquence la relation entre les fantômes est

.

 

36) enveloppe complexe des marques elles :

L'ébauche du antitransformed un du fantôme des marques elles traslato analytique pour porter f_{le c} dans l'origine, ha de laquelle ha et donc . L'enveloppe complexe a donc la portée à concourir de s'occuper les marque dans le s(t) de bande de traslata au moyen de deux membres dans la base de bande, elles l'écriture d'evincono elle-même en termes de vraie partie et partie imaginaire a en fait le membre dans la phase et le membre dans la quadrature, au moyen de ces membres les marque dans la bande de traslata peut être écrit dans la forme .

 

37) relation d'ortonormalità :

 

38) représentation des marques elles s(t) par une base :

là où {y_k(t)} est avec discret des fonctions et des coefficients c _k d'ortonormalide I sont choisis de diminuer l'erreur quadratique moyenne .

 

39) théorème de Nyquist - Shannon :

Admettre pour lui les marque s(t) sans limites dans le temps et limité dans la base de bande une représentation dans le dominion de la fréquence au moyen de la base obtient qu'elle peut être reconstruite pour laisser de la connaissance de I ses champions C_k = s(kTN) à condition que obtenu avec une fréquence au moins double de l'échantillonnage concernant la fréquence actuelle maximum à l'intérieur d'elle les marque, a l'infatti , l'intervalle de Nyquist est les marque dans ce cas-ci dans la bande de traslata peut être partir à la place reconstruit de la connaissance des champions de ses membres dans la bande la base s_c(t) et s_s(t) ayant le maximum de fréquence a en fait avec ED X = c, s et l'intervalle de Nyquist est dans ce cas divisé en deux .

 

40) N° des fonctions nécessaires afin de représenter n'importe quelles marques elles dans son intervalle de définition :

De lui il est nécessaire un nombre infini, toutefois pour quelques types de lui les marque peut être attrapé vers le haut d'une bonne exactitude également avec un nombre fini des marques elles, c'est la caisse de marques elles des limites de physiciens pratiquement à vous dans la bande et dans la durée pour laquelle un prélèvement avec un nombre des champions N=2BT étant B est suffisant la bande des marques elles physicien et T sa durée.

 

ORDRES Et ÉLÉMENTS de MARQUE ILS NUMÉRIQUES

41) ordre :

Avec lui est passé commande des valeurs qui peuvent être obtenues à partir de la marque elles le s(t) que continu considérant au lieu de le variable continuent la variable de t le NT discret où n il est la succession des nombres entiers, l'ordre générique a l'expression .

 

42) énergie pour des ordres :

 

43) puissance pour des ordres :

 

44) ordres d'intercorrelationship entre les ordres à l'énergie finie :

 

45) ordres temporels d'intercorrelationship pour des ordres de puissance :

 

46) ordres d'intercovarianza pour des ordres de puissance :

 

47) Alphabet De M-nario :

Les éléments d'un ordre numérique peuvent seulement assumer des valeurs concernantes à avec discret {s_q}, à chacun de ces valeurs peuvent être les associés des éléments d'un alphabet de M_nario {z_q} du cardinalità M qui en nature est une puissance de l'ossia 2 M = 2^b à pouvoir employer des alphabets avec le long peu binaire des mots b.

 

48) écoulement numérique :

Ébauche de la succession des symboles z_q concernant l'alphabet de M-nario, chaque associé un élément de l'ordre {s_q} et celui ils sont répétés avec le même temporizzazione kT.

 

49) période de symbole :

C'est l'intervalle du temps de T que les passages entre un symbole et le successif de l'écoulement numérique, son inverse est le rythme de symbole qui dans le cas à chaque symbole vient a associé un mot binaire constitué à partir du peu vient le rythme binaire défini dont l'inverse c'est la période du peu T_b .

 

50) il les marque à multiniveaux numérique :

Il marque des échantillons qu'ils à vous numérique présentent de dle (t) que pour être transmis ils exigent la moyenne à la bande infinie, afin d'obvier au ci² remplace dle (t) avec une fonction impulsive d'avoir une duréefinie par (t) de l'énergie f et pour ce qu'une limitation pratique dans la bande peut être obtenue en une telle obtention de manière les marque à multiniveaux numérique , comme exemple il est les marques obtenues ils numérique carré dans les utilisations de cas l'impulsion rectangulaire à l'énergie unitaire de ne pas les confondre avec des marques analogique carré .

 

51) vitesse de la modulation :

Elle les marque asynchrones que numériques sont tels pour lesquels les intervalles t_k entre un symbole et le successif le minimum des intervalles entre un symbole successif et ceux concernants à l'ordre ne sont pas constants ne peuvent pas donc être plus parlés qu'au rythme que le symbole mais au sujet de la vitesse de la modulation étant T _V. La vitesse de modulation est exprimée en baud et représente le nombre maximum des symboles de veicolabili des marques elles dans l'unité de temps.

GÉNÉRALITÉ SUR LES PROCESSUS STOCASTICI

52) quantité de l'information :

Dans le cas d'une source numérique la quantité de l'information est la taille associée au choix d'un symbole, z_q , entre M les éléments possibles qu'ils forment un alphabet de M-nario, lui vaut la peine d'être P(zq) la probabilité qui vient a émis le symbole z_q . La définition est logique si 0.1) les quantités d'equiprobabili [ p(0) = p(1) = 0.5 ] de l'information sont crues qui pour un alphabet binaire avec des symboles (soyez unitaire.

 

53) processus continu de stocastico :

Ses réalisations sont x(t) de fonctions continues qu'elles peuvent être émises de la source analogique. Pendant un moment des données T que le processus est réduit à un v.a. continue X_t = X(t) avec le p(X de densité de distribution_t , t).

 

54) processus discret de stocastico aux valeurs discrètes :

C'est le cas d'un écoulement numérique émis d'une source numérique, est le temps que la valeur des réalisations n'est pas continue mais discrète.

 

55) densité de la probabilité combinée de 2° l'ordre :

exprime la probabilité qu'au temps t₁ a lieu X₁ comporté entre x₁ ED X₁ dx₁ et au temps t₂ X ont lieu₂ comportés entre le dx_{2 2} de x₂ EDX , où X₁ et X₂ est deux ceux aléatoires variables qui sont obtenus à partir du processus de stocastico fixant le temps dans les moments t₁ et le t₂ .

 

56) densité de la probabilité conditionnée de l'ordre n :

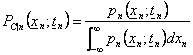
dans la variable courte le X_n au temps t_n il est conditionné de la connaissance du v.a. émis dans les moments précédents.

 

57) processus de Markoff de l'ordre n :

C'est un processus dont la pleine connaissance a lui-même si la densité de la probabilité combinée de l'ordre est n connu 1.

 

58) valeur moyenne statistique :

 

59) statistiques moyennes de puissance :

 

60) désaccord :

.

 

61) relation entre le désaccord et la puissance :

 

62) fonction des statistiques d'autocorrelationship :

 

63) fonction des statistiques d'autocovarianza :

pour t₁ = t₂ l'autocovarianza coïncide avec le désaccord.

 

64) relation entre l'autocovarianza et l'autocorrelationship :

 

65) processus stationnaire dans le sens serré :

C'est un processus pour lequel la densité des probabilités invariables est respect à une traduction temporelle arbitraire.

 

66) processus stationnaire parlant largement :

C'est un processus pour lequel on a la densité des probabilités invariables est respect à une traduction temporelle arbitraire, alors que la densité de la probabilité combinée de l'ordre 2° dépend seulement de t, qui est :

)       p(x;t) = p(x) b) p₂(;tde x₁,x₂₁,t2) = p₂(x₁,x₂;t) essendo t = t₂ - t₁

pour un processus stationnaire le parler largement est eu que les statistiques moyens de valor, la puissance et le désaccord sont constants et correspondent aux valeurs prévues des largenesses temporels de correspondants pour une réalisation simple du processus tandis que les fonctions de l'autocorrelationship R(t) et de l'autocovarianza K(t) dépendent en solo de t.

 

67) relation entre l'autocovarianza et l'autocorrelationship pour des processus stationnaires :

 

68) première relation de saucisse - Khinchine :

ce membre spectral discret dans l'origine démontre donc un.

 

69) processus stationnaire d'ergodico :

C'est un processus pour lequel la réalisation simple, observé sur l'axe entier des temps, ajoute toutes les statistiques de propriété du processus aléatoire, donc lequel les largenesses temporels convergent aux statistiques de largenesses.

 

70) la densité spectrale de intercrossed la puissance :

 

71) seconde relation de saucisse - Khinchine :

 

72) caractéristique de la somme de processus d'a(t) de stazionari de deux processus = de y(t) de x(t) :

Considérant le y(t) de processus d'a(t) = de x(t) le valor est h statistique moyen eu = h_x h_y tandis que l'autocorrelationship est donc la somme stationnaire de processus est également lui. La densité de puissance est donc le cône de deux de processus simplement cumulateurs de sommabili dans la puissance s'ils sont orthogonaux ou si .

 

73) caractéristique de y(t) de processus complexe de b(t) = de x(t) j :

Considérant le jy(t) de processus de b(t) = de x(t) _{le x} sont valor eu h statistiquemoyen _b =h jh_y tandis que l'autocorrelationship est donc le processus complexe est également stationnaire il. La densité de puissance est .

PROCESSUS STOCASTICI CICLOSTAZIONARI

74) processus de stocastico de ciclostazionario :

L'ébauche d'un processus dont la fonction de l'autocorrelationship est périodique dans t, en particulier est parlée au sujet des processus de ciclostazionari de 1° l'ordre si la régularité est présente également dans statistique moyen de valor et les processus de ciclostazionari de 2° que l'ordre s'il est présent choisissent dans l'autocorrelationship. L'analyse peut être menée de nouveau à celui-là des processus stationnaires effectuant une traduction z sur l'axe des temps et effectuant un indépendant de milieu mais l'uniforme de telles statistiques également sur v.a. dans la période, d'une telle manière h_s et R_{solides solubles}(t) est estimé comme des valeurs moyennes des fonctions périodiques respectives dans t .

 

75) les processus représentent à vous par l'enveloppe complexe :

Avoir la réalisation de processus est stationnaire si les deux processus composants sont conjointement stationnaires tandis que c'est ciclostazionario s'il il est également l'un seulement d'eux, l'autocorrelationship est

donc tandis que le processus est dans un ciclostazionario généralisé de façon dans combien son autocorrelationship négocié une période coûte et a l'intensité de la puissance.

 

76) processus stationnaire dans la bande de traslata :

Étant stationnaire le processus de S(t) dans la bande de traslata on l'a qu'également les processus dans la bande basent S_c(t) et S_s(t) est parler largement stationnaire avec des fonctions identiques de nulle de milieu d'autocorrelationship et de valor. On le gagne que la puissance n'est pas divisée sur les deux processus mais est trouvé encore identique sur chacun d'eux.

 

77) les vrais processus avec des facteurs aléatoires représentent à vous au moyen de série temporelle :

Un processus de S(t) est considéré avoir la réalisation être déterminationvariable aléatoire continue de z _k du Z_k qu'ils forment avec leur ordre de Z(n) un vrai processus discret stationnaire tandis que la vraie fonction de p(t) est une ayant la durée pratique T_p . D'une façon généralisée S(t) est un processus de ciclostazionario ayant le milieu de valor , l'autocorrelationship et la densité spectrale de la puissance. La puissance du processus est simplement dans le cas est orthogonale le v.a. z_k ou elle les marque les cumulateurs d'énergie qui constituent la forme périodique.

 

78) échantillon de processus dans la base de bande à vous :

C'est un cas particulier de la situation précédente, considère en fait un processus dans la bande ayant la réalisation basse 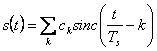de S(t), obtient que le valor h statistique moyen il est égal au milieu h de valor que_{le c} du processus discret a constitué à partir de l'ordre des champions aléatoires tandis que la densité spectrale de la puissance est .

 

79) processus de complexe avec des facteurs aléatoires :

Nous considérons un processus continu vrai ciclostazionario dans la bande de traslata que la réalisation est associé l'enveloppe complexe de processus ayant, la densité spectrale de la puissance associée à elle est :

 

80) somme de processus de vrais processus avec des facteurs aléatoires :

Un processus de S(t) est eu avec la représentation dans la forme, la corrélation d's'avérer est .

 

81) processus continu gaussien :

C'est un processus dont la pleine connaissance a lui-même des statistiques simples basées sur la connaissance de la fonction de densité de probabilité de 2° l'ordre, dans le cas de stazionarietà l'expression de la densité de la probabilité de 1° que l'ordre est . Une propriété importante de ce processus est que la somme de processus gaussiens indépendants est toujours un processus gaussien avec la somme moyenne de valor des valeurs moyennes et la somme de désaccord des désaccords d'ailleurs la somme de n arbitraire mais les processus indépendants est un processus gaussien pour le ¥ ® de n ont en second lieu affirmé combien du théorème de la limite les centre.

 

82) Bruit Gaussien :

C'est le processus gaussien s'avérant de la somme de nombreuses marques qu'ils aléatoires précise à vous, en particulier nous ont un homme blanc de bruit gaussien si la densité spectrale de la puissance est N(f) = Nconstant ₀ = que l'autocorrelationship correspond .

 

83) bruit gaussien stationnaire dans la bande de traslata :

Nous considérons une représentation générique du bruit dans le traslata de bande , les processus stationnaire gaussien dans de bandebaseN _c (t)etd'alerte de N _s (t) et la puissance du bruit dans la bande de traslata est trouvés encore identiques sur chacun d'eux tandis que la densité spectrale présente une diverse largeur de bande à la deuxième de pendant qu'elle vient f choisi_c , est en particulier maximum et égale à 2B si f_c est à une des extrémités de la bande de traslata tandis qu'il est minimal et égal à B si f_c est le centre de la bande de traslata.

 

84) homme blanc de bruit gaussien dans l'espace des marques elles :

Dans l'espace avec la dimension de N tendant à l'infini, une réalisation de l'homme blanc de bruit est rappresentabile avec avoir le ciascuna de membres du porteur n avec la densité de la probabilité de l'ordine 1° .