Processus de Ciclostazionari
1) processus de ciclostazionario dans le sens serré :
C'est un processus non stationnaire pour lequel un vrai
nombre T
0 >0existe, a dit la période du ciclostazionarietà, tel
que la densité de la probabilité combinée vérifie 
où avec xn'elle signifie xn pour chronométrer t1 T0 .
On l'a que tous les moments statistiques du processus de ciclostazionario sont des fonctions périodiques avec la période T0 .
2) processus de ciclostazionario parlant largement :
C'est un processus non stationnaire pour lequel la
densité de la probabilité du 1° et du 2° l'ordre s'avère
périodique dans le statistique moyen de temps et par conséquent
également de valor et la fonction de l'autocorrelationship qui peut
donc être se développe à vous en série de Fourier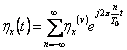 
où 
est la fréquence cyclique.
3) Valor moyen cyclique :
4) fonction d'autocorrelationship cyclique :
5) densité spectrale de puissance cyclique :
Vu une réalisation simple elle est eue
là où XT(f,t0) est transformé
de Fourier de la restriction du x(t) de processus à une durée de T
autour à t0 tandis qu' est la fréquence cyclique.
6) première relation de Khinchine généralisé par saucisse :
7) processus de cicloergodico dans le sens serré :
C'est un processus pour lequel toutes les moyennes temporelles coïncident avec les statistiques moyennes de correspondants négociées la période.
8) processus de cicloergodico parlant largement :
C'est un processus pour lequel l'ordre di1° et 2° temporel
de moyennes coïncident avec les statistiques moyennes de
correspondants négociées la période, en particulier 
e
est eu.
9) fonction d'intercorrelationship cyclique :
Dans le cas de deux processus de ciclostazionari parlant largement avec la même période T0 , ha
.
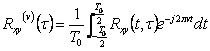10) la densité spectrale de intercrossed la puissance cyclique :
11) la seconde relation de la saucisse a généralisé Khinchine :
12) processus stationnaires et de ciclostazionari dans le VHF :
L'autocorrelationship du processus dans le x(t) de VHF
peut être exprimé en termes de processus en base moyenne de bande
nulle au valor Xp(t) en phase et
xq(t) dans la quadrature, est
eu 
célèbre donc qui indépendamment de I traite xp(t) et xq(t) le processus dans le x(t) de VHF s'avère être
ciclostazionario parlant largement avec la période 
.
La moyenne temporelle de la fonction d'autocorrelationship est 
quelle densité spectrale de potenza correspond
un 
.
Les deux cas particuliers suivants peuvent être eus :
) si les processus dans la base de bande
sont alors également x(t) stationnaire sont stationnaires et 
e 
est eu
donc l'autocorrelationship est réduit à 
et donc la densité spectrale de la puissance est 
.
On l'observe que pour t = 0 il est obtenu pour la densité de la puissance 
et pour les désaccords 
donc xp et xq ils sont des processus orthogonaux et leur densité de la
probabilité combinée est le produit simple de la densité de la
probabilité, dans le cas qu'ils sont gaussiens ont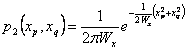 
et étant 
et 
coordonnent un changement de avec Jacobiano J = r qu'elle
donne en arrière, saturant 
concernant l'ottiene
de j qui
est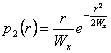 
un peut être fait densité de la probabilité
du type de Rayleigh tandis qu' saturant le respect à r 
est trouvé qui est une densité de la probabilité du type
uniforme donc que le croisillon de la variable est statistiquement
indépendant. D'ailleurs la densité de la probabilité de la
puissance instantanée de processus 
est
exponentielle 
.
b) si les processus dans la base de
bande sont ciclostazionari et supposant pour le semplicità Xq(t)=0, la fonction de
l'autocorrelationship sont 
est à qui
autocorrelationship moyen 
ce qui la densité
spectrale de la puissance 
donc au fantôme
correspond des marques qu'elles dans le VHF correspond également les
fantômes cycliques des marques elles dans la base de bande.
13) statistiques de propriété de l'oscillation harmonique en présence de bruit gaussien :
L'expression du processus dans le VHF en présence de pur
une oscillation harmonique est 
escroc 
, vient d'ailleurs défini l'autocorrelationship 
et la fonction du pseudocorrelation 
qui
concourt pour écrire l'autocorrelationship du x(t) dans la forme 
qui s'avère être périodique avec 
la période donc le processus est ciclostazionario parlant
largement car il était expectable pour la présence du membre
harmonique.
L'autocorrelationship moyen est 
à qui
transformé de Fourier c'est la densité spectrale de la puissance et
démontre la superposition entre le fantôme de l'oscillation
harmonique et le fantôme du bruit dans le VHF. Si les processus
dans la base de bande sont gaussiens, la densité de la colombe
combinée 
de probabilité 
est
eue, par le changement de coordonné 
, 
ayant Jacobiano J = r est atteinte la forme
que, saturé concernant des retours de j 
tandis que le respect
saturé à r il donne 
avec 
,
finalement la densité de la probabilité de la puissance instantanée
de processus est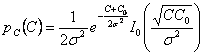 
.
14) fantôme de la puissance des marques elles dans la base de bande :
On le suppose que les marques elles de la puissance dans
la base 
de bande à oùà k c'est un processus discret stationnaire parlant
largement avec les statistiques h , Rà , s2 tandis que le q(t) il est des marques elles
de l'énergie transformée avec de Fourier Sq(f) et de l'énergie 
la
valeur moyenne du x(t) est 
et est donc
périodique avec la période pures de T comme la fonction
d'autocorrelationship 
à partir quelle intégration sur Ts l'autocorrelationship cyclique avec
v=0 est obtenu qu'un changement variable de remplisseur à la forme 
(…où etq(t) il est
l'autocorrelationship des marques elles du q(t) d'énergie) pour
lequel a estimé t= 0 et
remplacement 
il fournit la puissance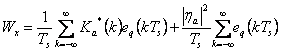 
tandis que la densité spectrale de la puissance est
transformation obtenue selon Fourier RX(t), obtient 
qui est un fantôme aux lignes recouvertes à un fantôme
distribué.
On l'observe que si le processus {à
l'hommeblanc de}è de k ou si le q(t)
est aux cornues orthogonales, la puissance du x(t) de processus de
ciclostazionario est égale au rapport entre l'énergie de la forme de
la vague de determinist et la période sde T qui est 
.
15) il les marque dans la base généralisée de bande :
La forme plus générale que les marque dans le x(t) de
base de bande est obtenue comme la combinaison des formes de M de ciascuna
extraitde l'énergie X j avec la probabilité a priori P et avec la cadence sde
T , est eue 
c'est-à-dire,
là-dessus vient a défini le symbole moyen 
qui
dans le cas les marque vient représente à vous dans l'espace des
marques qu'elles coïncide avec le barycentre de la constellation des
symboles. Le fantôme qui d'elle s'avère est donné de la
superposition d'un fantôme continu et d'un fantôme distribué, peut
être interprété comme le fantôme de la puissance de la forme de la
vague périodique 
qui coïncide avec la valeur
prévue du x(t) qui est 
et qui être périodique
il peut être décomposé en série de Fourier 
où Sà (f) est
transformé de Fourier de l'image de module 
de
symbole moyen lequel donne en arrière la densité spectrale de la
puissance aux lignes 
et donc célèbre qui le
fantôme des marques elles périodiques il est discret et elle
possède les lignes multiples entières de la fréquence de
symbole.
16) le fantôme de la puissance deux les marque dans la base de bande :
Il les marque que la somme de deux les marque dans la
base de bande est 
dans quel autocorrelationship
cyclique avec le ciclicità 
v=0 correspond cela
estimée t = 0 donne en
arrière la puissance 
où intercrossed la
corrélation vaut la peine 
le quindi 
.
Transforme selon Fourier l'autocorrelationship cyclique 
a plongé 
, 
est obtenu, remplaçant pour la
dernière fois les trois expressions dans le Wz obtient une relation que dans le cas des hommes
blancs de processus avec h= 0 e sà 2 = à 1 sont ramené 
au de quelle intégration le potenza 
obtenu.
17) représentation géométrique des processus aléatoires
Un x(t) de processus aléatoire moyen à la nulle
de valor peut être représenté dans un intervalle fini 
par le développement en série 
où yk(t)
est avec des fonctions d'ortonormali de n dans 
l'intervalle tandis que {ck} est un processus aléatoire discret au nulo moyen de
valor, si présente 
la corrélation le
développement est dit en série de Karhunen-Loeve.
Dans le but pour trouver une équation qu'elle concourt
pour déterminer yk(t) il calcule l'intercorrelationship entre le x(t) et le
c kde processus , a 
du repos pour les coefficients c kde I peut être écrit la
relation 
, le remplaçant dans le calcul de
l'intercorrelationship a 
l'uguagliando que les
deux ont trouvé des expressions obtient un système des équations à
l'autofunzioni 
qu'ils doivent satisfaire
l'autofunzioni de la base yk(t).
L'égalité est une égalité entre les
processus et doit vérifier que la convergence quadratique à la
moyenne 
cependant dans le cas du développement
kilolitre a 
qui est démontré pour être condition
nécessaire et le suffisamment d'affinchè la convergence quadratique
à la moyenne est respecté. Par les substitutions
, 
, 
le système des équations vient normalisé qui est mené de nouveau à l'intervalle [ - 1, 1 ], est eu :
là où le ck est des fonctions orthogonales dans l'intervalle [
- 1.1 ].
Les deux exemples suivants de l'application sont faits :
) représentation de l'homme blanc de bruit dans un intervalle fini
La fonction de l'autocorrelationship du x(t) est 
avec 
être NX la densité spectrale du processus
bilatéral, remplaçant obtient le système des équations 
qu'il a comme solution de ledit sphéroïdal de fonctions
écrasé.
b) Représentation de l'homme blanc de bruit de la durée infinie
La fonction de l'autocorrelationship du x(t) est avec être NX la densité spectrale du processus
bilatéral, mais dans ce cas-ci elle est faite pour étirer à infini
l'intervalle d'intégration, remplaçant dans 
et
tirer profit de la relation 
N
Xest q obtenu k= et traite donc {ck} s'avère parler largement
stationnaire, il trouve d'ailleurs que la relation 
est vérifiée et donc la convergence
quadratique à la moyenne est eue.