Vibrations réticulaires

1) vitesse de groupe :

Ébauche du dérivé de la pulsation angulaire W concernant le porteur de la vague k .

 

2) les caractéristiques de propagantesi d'une vague élastique dans une chaîne ont formé des atomes égaux :

On le suppose que des mises à niveau elles du type élastique où x sont le mouvement donc la force temporaire soyez .

Nous considérons une chaîne linéaire d'atome que vous expédiez à une distance à entre d'elles, la force que les actes sur l'atome en position s due à l'atome dans la position s p est proporziona elles par C constant_p à la différence de leurs mouvements_États-Unis et_{États-Unis p} concernant les positions de l'equilibrio .

Considérer pendant que l'origine le commencement de la chaîne et des solutions de recherche du sinusoidale dactylographient et le remplacement dans l'équation les différencie qu'elle a et le dividende pour obtient où l'interaction avec des atomes égaler bien à l'interaction avec des atomes a été considérée du côté gauche. S'il est limité à nous à l'interaction avec les premiers voisins simples donc p = 1 et la limite dans la parenthèse comme un sein est écrit, la relation de la dispersion est obtenue.

 

3) zone 1ª de Brillouin :

Écrivant le rapport entre la valeur du mouvement dans un point_{États-Unis p 1} et la valeur du mouvement dans le point précédent_{États-Unis p} un trouve et^l'ika que c'est une quantité périodique avec la période 2p de à ce qu'ils nous intéressent est des valeurs positives que vous que les valeurs ont refusé à vous pourquoi les vagues mettent en boîte propagar êtes vers la droite qui du côté gauche le £ p de kade £ donc - p étant à la distance entre 2 atomes de la chaîne. est eu qui représente la première zone de Brillouin.

 

4) caractéristiques de la relation de dispersion :

Nous avons vu vient obtenu vu l'interaction simple avec les premiers voisins dans le cas d'une chaîne formée des atomes égaux, les ha desquels pu² pour gagner la vitesse de groupe 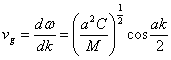dont célèbre cela dans la correspondance au bord de la zone a v_g= 0 et donc nous sont en présence d'une vague debout.

 

5) rapport entre v_g , v_s et la relation de la dispersion :

le pu² de vitesse de groupe pour se gagner de la relation 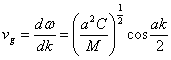de la dispersion. Pour k petit qui est dans la bande acoustique on l'a que le diagramme de la relation de dispersion est assimilable à un droit et donc

 

6) les caractéristiques de propagantesi d'une vague élastique dans une chaîne ont formé de 2 ayant les diverses masses d'atomes :

On le suppose d'avoir une chaîne linéaire constituée à partir d'une alternance d'atome avec la masse M₁ et des atomes avec la masse M₂ , l'interaction de l'atome avec l'endroit de la masseM ₁ en position 2s 1 avec les premiers voisins est donnée du differenziale d'équation :

Analogue l'interaction de l'atome avec l'endroit de la masseM ₂ en position 2s avec les premiers voisins est donnée de l'équation :

Ébauche de 2 équation diffère ils pour quel nous essayent solution dans forme de deux ayant sinusoidi même pulsation mais divers amplitude pour avoir atome divers le masse qui est e qui a remplacé dans les équations différencie elles des dommages système dans incognito x et h qui ont la solution simple si de détermination est décommandée qui est si de ce qu'on gagne le que pour chaque W 2 les diverses valeurs de k existent et analogue pour chaque k existe 2 diverses valeurs de W en particulier que la solution avec le signe va à décrire W aux correspondants plus hauts à la branche optique qui assume la valeur maximum pour k=0 et la valeur minimale sur les bords de zone. La solution avec le â "elle caractérise à la place la branche acoustique qui est beaucoup semblable à la courbe de la dispersion trouvée dans le cas d'une chaîne identique d'atome. Entre les 2 branches est une branche interdite.

 

7) la première zone de Brillouin dans le cas d'une chaîne a formé de 2 ayant les diverses masses d'atomes :

Écrivant le rapport entre la valeur du mouvement dans un point_{États-Unis p 2} et la valeur d'avoir le mouvement dans le point précédent les mêmes trouvailles_{des États-Unis p} de la masse et^ik2a que c'est une quantité périodique avec la période 2p de à ce qu'ils nous intéressent est des valeurs positives que vous que les valeurs ont refusé à vous pourquoi les vagues mettent en boîte propagar êtes vers la droite qui du côté gauche le £ p du £2ka donc - p étant 2a la distance entre 2 ayant des atomes de l'à chaînes la même masse, dans les formules a .

 

8) caractéristique des manières optiques :

Plaçant k=0 dans l'équation de la branche optique et remplaçant dans elle les équations du système dans x et h est trouvé donc les atomes vibre dans l'opposition de phase.

 

9) caractéristique des manières acoustiques :

Plaçant k=0 dans l'équation de la branche acoustique et remplaçant dans elle les équations du système dans x et h est trouvéx = h donc que les atomes vibre dans la phase.

 

10) conditions à la découpe de Karmann :

Le champion est limité doit donc supposer pour joindre les extrémités et donc exiger que la vague assume la même valeur est au commencement de la chaîne pour s=0 qui à l'extrémité pour le s=L. est eu qui est seulement vérifié pour assurer a donc une quantification sur le k. Afin de trouver le nombre n du k vous concourez vous-même dans 1ª assez la zone pour multiplier la densité des états en k à l'unité de la longueur pour la longueur de 1ª la zone, a l'égale qui est au nombre d'atome donc que le k sont quantizzati mais ils rapprochent continu. Analogue l'amplitude de 1ª que la zone peut être divisée pour la distance entre deux k est concourue .