Propriété thermique des isolateurs

1) capacités thermiques au volume constant et à son classique de diagramme :

Il est défini comme le dérivé partiel de l'énergie intérieure et de considérer la température de T au volume constant . Pour la mécanique classique, l'énergie d'atome intérieure chaque est association estimée à chacun de ses 6 degrés de liberté (traslazionali 3 vibrazionali et 3) que une énergie donc considérant un atome classent l'énergie intérieure est et donc constante donc avec la température. La confrontent avec les aperçus elle les éprouve obtient que cette représentation sensiblement est corrigée aux températures élevées tandis qu'aux terres en contre-bas, les capacités thermiques il y a des bouts droits à 0 et comme T³ , il est nécessaire d'expliquer un tel comportement de considérer l'énergie intérieure due à la simple fononi, parce que chacun d'eux a donc le total d'énergie est colombe 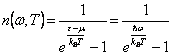(où m = le 0 dans combien de fononi les particules manquant dans la masse) sont la fonction du métier de Bose qui décrit le n° du fononi que à un indiqué la température les possèdent la pulsation W_k mais nous ont attendu que comme k ait contenu dans 1ª la zone qu'elles rapprochent continu peuvent donc être remplacées la récapitulative avec une intégrale. Une difficulté d'une telle intégrale réside dans le D(w), elle peut expérimentalement être obtenue et l'intégrale délibérée numériquement ou les approximations d'Einstein et de Debye sont employées.

 

2) N° du métier du fononi :

Le fononi elles sont de bosoni donc le nombre du fononi que à un donné au posseggono un de la température donné énergie l'est donné des statistiques de Bose Einstein . Une considération importante pour faire qu'elle est à la base de l'hypothèse de Debye est que quand on a®T 0 que le nombre du fononi est élevé pour W petit et donc de la relation de dispersion, pour k petit.

 

3) densité linéaire des états en k :

Nous avons gagné des conditions à la découpe de Karmann qui la distance entre deux k que vous concourez vous-même consécutif est , afin de trouver le w(k) de densité assez du k pour faire de le mutuel obtenant .

 

4) hypothèse d'Einstein :

Einstein propose une densité suivante des états dans W de type, c'est que chaque fonone il possède la même pulsation W=_einsteinde W=W_et donc vu une taille de N de fononi, dont chacun (s'il vaut la peine la loi de Hooke) possède 3 manières indépendantes dont de vibration (2 ceux en coupe et un longitudinale ) est eu d'elle est eu regarde cela pour le ¥®de T que l'exponentiel peut être développé en série et C est _vtrouvé®3Nk=3R tandis que pour T®0 l'exponentiel au dénominateur diverge et donc C_v®0 comme un exponentiel et pas comme T³ qui est la valeur les éprouve, ceci a doit la mauvaise approximation du D(w) qui cependant pour les températures élevées elle est de la préférence à l'approximation de Debye.

5) expression de la densité des états dans W dans le cas d'une chaîne linéaire :

Observant la courbe de dispersion il est nécessaire de mettre dans la relation que la densité des états dans W D(W) avec la densité des états en k a l'allora . Remplaçant l'expression du V_g qu'on l'obtient à partir de la relation de dispersion voit que le D(w) diverge au ¥ dans la correspondance à l'asymptote vertical W = W_maximum . Avec l'approximation de Debye le D(is a constaté quew) est constant jusque 2'à la valeur W_D .

 

6) hypothèse de Debye :

Debye observe de la fonction du métier de Bose 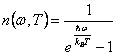qu'aux basses températures (..sono les températures qui intéressent parce qu'avec eux les capacités classiques sont confondues) sont beaucoup de le fononi avec du k petit, mais dans ces régions la courbe de dispersion peut être rapprochée avec 2 tangentes droites à la limite pour k®0. Les effets de cette approximation sont 2 :

)       se rappeler cela a la constante et donc pu² à porter dehors de l'intégrale de C_v .

b)       Ils changent en les fins de l'intégration dans combien la tangente droite rencontre le dépassement vertical pour le bord de la zone pour W_D > W_maximum ha W_D = le W 1.57_maximum .

Effectuant les calculs C _v0®comme T ³est trouvé .

 

7) densité superficielle des états en k :

Il est , est obtenu de la manière analogue au cas d'unidimensionale.

 

8) considérations sur l'approximation de Debye dans le cas bi-dimensionnel :

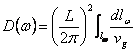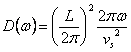Le D(is écritw) considérer des lignes à la constante de W, obtient , afin de la simplifier selon Debye v sont placés_g = v_s et la porte dehors de l'intégrale et d'ailleurs rapproche la courbe de la dispersion avec un cercle du faisceau k donc qui a remplacé dans l'intégrale concourt pour calculer l'énergie intérieure. Vous vous notez que la fin avançée de l'intégrale est W_{le D} qui est uguagliando obtenu le nombre de fononi au produit entre la densité du fononi à l'unité de la surface pour le secteur de la circonférence de Debye. Comme résultat obtient que la densité des états est en croissant dans W jusque 2' à W le correspondant au bord du dopodichè de la zone 1ª elle diminue jusqu'à être en valeur 0 dans la correspondance à la valeur du faisceau de la circonférence rapprochante.

 

9) densité de volumica des états en k :

Il est , est obtenu de la manière analogue au cas d'unidimensionale.

 

10) considérations sur l'approximation de Debye dans le cas tridimensionnel :

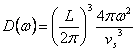Le w) écritpar D(is considérant les superficiels à la constante de W, obtient , afin de la simplifier selon Debye v sont placés_g = v_s et la porte dehors de l'intégrale et d'ailleurs rapproche la courbe de la dispersion avec une sphère du faisceau k donc qui a remplacé dans l'intégrale concourt pour calculer l'énergie intérieure. Vous vous notez que la fin avançée de l'intégrale est W_{le D} qui est uguagliando obtenu le nombre de fononi au produit entre la densité du fononi à l'unité de volume et le volume de la sphère de Debye. Comme résultat obtient que la densité des états est équation quadratique en croissant dans W.

 

11) la température de Debye :

C'est une mesure de la force de la cravate qui caractérise le bonnet, plus grande est la température de Debye, plus grande est la force de la cravate. Il est obtenu à partir de la relation, est donc la température qui correspondà W_{le D} .

 

12) causes de la dilatation thermique de la pleine :

Les forces de l'interaction entre 2 atomes ne sont pas décrites d'un oscillateur harmonique donc d'une parabole puisqu'à elle un linéaire correspond pour ce que donc il vaut la peine la superposition des effets mais d'une fonction plus complexe et surtout plus asymétrique, donc un atome qui à la suite du somministrazione de la chaleur oscille autour dans la position d'équilibre, il y a de la manière asymétrique dans les 2 directions et donc le mouvement moyen n'est pas nul et donc la chaîne linéaire est dilaté.

 

13) coefficient de conductivité thermique K :

C'est le coefficient de la proportionnalité de K entre la quantité de la chaleur de Q que les écoulements dans un matériel et le gradient de la température dans le présent il, a . Afin de gagner la valeur de K on l'observe que la quantité de la chaleur transportée de n ayant les capacités thermiques c de ciascuna de particules est , du repos où t le temps est la période de la relaxation qui est que les passages entre 2 coups sont arrivés à vous, d'ailleurs vu qu'une surface unitaire est eue que dans l'unité de temps il est croisé de n|v_x| le fononi tout à fait dans les deux dos donc est eu où l'isotropia a été supposé donc . Étant le l=vt la manière et le C=nc moyens libres le total thermique de capacités du système est eu donc .

 

14) manière moyenne libre du fononi :

C'est la distance moyenne qu'ils couvrent entre une collision et la successive, est fonction des causes suivantes :

)       présence dans le divers bonnet d'atome qui isotopes ou impurità

b)       Limitatezza physique du bonnet

c)       Collision entre le fononi

 

15) lois de conservation dans une collision entre le fononi :

Loi de conservation presque du moment

Loi de la conservation de l'énergie

L'attention, n'est pas nécessaire que le nombre de fononi conserve.

 

16) typologie des coups entre le fononi et la manière moyenne libre :

Quand le fononi 2 ils sont venus pour trouver dans la même région les espace, une collision est eue dans laquelle elle doit être conservée la quantité d'énergie et de l'impulsion, les 2 types suivants de collision peut être vérifiée :

)       collision normale elle est eue quand le k s'avérant de la somme vectorial du k du fononi les incidents le fonone est contenu dans 1ª que la zone d's'avérer est donc toujours dans la direction du mouvement et contribue à la conduction thermique.

b)       La collision d'Umklapp est eue quand le k s'avérant de la somme vectorial du k du fononi les incidents il sort de 1ª la zone mais le sottraendogli un porteur du bonnet mutuel obtient un fonone avec du k tels de l'opporsi au mouvement. Le fononi utile ils sont ceux qu'ils ont k à côté du bord de 1ª la zone, leur nombre accroît linéairement avec la température en fait donc le descresce de conductivité thermique linéairement avec la température.

 

17) imperfections et manière moyenne libre :

L'effet des imperfections a l'endroit quand la manière libre moyenne qui a du les processus d'Umklapp est comparable aux dimensions physiques du cristal, donc la manière moyenne libre est seulement constante avec la température.

 

18) valeur de la conductivité thermique en fonction de la température pour un isolateur :

La variation est nécessaire pour analyser du coefficient de l'courant ascendant de conductivité avec la température, elle a cela aux températures élevées que le processus prédomine d'Umklapp dans combien de fononi efficace devient pour se développer de la température, aux températures à côté de la température du nombre de Debyeq _D de diminutions efficaces de fononi comme le négatif exponentiel, tandis que si T®0 le nombre de bouts droits efficaces de fononi au zéro et donc manière moyenne libre est constant dans combien d'impôt des imperfections et des dimensions du cristal qui est constant, et domine donc les capacités thermiques C qui poussent la conductivité thermique à zéro comme T³.

 

19) typologie des sondes utilisables afin d'analyser les caractéristiques du fononi :

)       l'électron qu'être non neutre a le problème et donc il est valide seulement pour une analyse superficielle du matériel.

b)       l'annulation électromagnétique et en particulier I rayonne x.

c)       il sont difficiles se produire et arrêter les neutrons qui réagissent faiblement aux champs magnétiques mais.