Propriété des métaux

1) modèle de Drude :

Tous les atomes du métal sont qui font l'utilisation, ont donc un électron simple sur la couche plus externe, elle faiblement sont attirées du noyau ambiant donc déjà à la température vont loin de l'atome d'origine, qui se produit pour tous les atomes et elle est venue donc pour créer un nuage d'électron qui facilite est les conductions thermiques qui les ouvriers électriques et l'acte comme de l'adhésif pour le bonnet cristallin. Le modèle est en position à expliquer les linéarités de la loi de l'ohm dans combien soutient que l'électron accéléré d'un champ électrique externe vient sans interruption pour frapper contre le ionien du bonnet et le pertando se déplace avec une vitesse de la dérive v_d . Avec cet ouvrier électrique modèle se trouve pour la conductivité.

 

2) loi de Wiedemann - Franz :

en fait 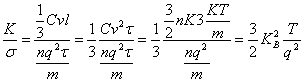est eu où être a été remplacé l'énergie classiquement associée à chaque fonone tandis que v obtiennent à partir de l'égalité entre l'énergie thermique et l'énergie cinétique .

On l'observe qu'il y a des linéarités dans les comparaisons de la température et qu'elle est valide pour n'importe quel matériel dans de combien coûte indépendant le nombre de Lorenz . L'ébauche d'une loi qui vient s'est développée en termes de périodes de relaxation et qui il est trouvée expérimentalement et soutient donc le modèle de Drude.

 

3) non explicable problématique avec le modèle de Drude :

)       les capacités thermiques qu'elles des métaux basés sur le modèle des expériences de Drude devraient être avancées de 50% aux capacités thermiques aux isolateurs en fait dans les métaux là-bas à la contribution 3R de fononico ont également la contribution électronique . Que met dans la crise le modèle de Drude en fait pour un isolateur a eu tandis que pour les métaux essentiellement identiques est trouvé expérimentalement donc à moins qu'à de basses températures où un cours linéaire et non cubique a lui-même.

b)       l'effet de hall dont desume que les porteurs de la charge pas nécessairement ils sont des électrons.

 

4) Effet De Hall :

Un champ est appliqué et_x à un conducteur couvert du courant, plongé dans un domaine de l'induction magnétique B dirigée le long de z, les frais dans le mouvement sont sujets à la force de Lorentz qu'il pousse à eux vers une paroi latérale du conducteur, cette séparation des frais donnent à l'endroit à un champ électrique qui travaill dans le sens opposé, au régime obtiennent donc un équilibre entre l'effetti deux à partir duquel la constante de Hall est obtenue .

 

5) modèle du gaz de la société des électrons libres :

Le métal est vu comme un scato il vide (prive du bonnet) à l'intérieur duquel il y a les fermions qui n'ont pas de l'interaction entre d'eux, ceci est la raison pour laquelle il est parlé au sujet du gaz. Pour dire le gaz l'énergie cinétique simple est appliquée à l'équation de Schroedinger considérant dans le Hamitoniana donc la courbe de et selon k la parabole est une. Dans l'unidimensionale le cas est eu, si de lui qu'ils essayent des solutions dans la forme de l'esponenziali complexe imposant alors ce y(x) assume des valeurs égales aux deux extrémités, en accord avec les conditions de Karmann a la quantification du k, en fait elles sont valides seulement le k tels que . D'ailleurs soyez une question des fermions vous qu'elles peuvent être deux d'elles avec le même un purchè de k ont la rotation vis-à-vis de.

 

6) considérations sur l'impulsion de l'électron libre :

La théorie de schroedinger affecte à l'impulsion l'opérateur, il doit vérifier que la relation avec est obtenue .

 

7) énergie de société :

Ébauche du correspondant d'énergie au porteur k du dernier électron inséré. Afin de le gagner on l'observe que l'énergie dans le cas de gaz de la société est et d'ailleurs la valeur de k obtient imposer cela au commencement et l'extrémité de la chaîne la fonction assume la même valeur et donc que pour les conditions de Karmann est trouvé mais pour la symétrie de la parabole on l'a qu'à chaque niveau n 4 de quantico sont offerts de n les électrons donc et du repos de L=Na où L est la longueur de la chaîne linéaire et à la séparation entre un atome et le successif donc il a de quel ottiene .

 

8) fonction de distribution ferme de Dirac :

Il vaut la peine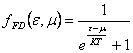 où m sont mise à niveau ils le produit chimique qui est égal à l'énergie de la société seulement à 0K.

 

9) quant à calculez-le les améliore produit chimique :

Si vous notez N et D(etassez) imposant .

 

10) point de société :

C'est un point de l'axe du k qu'il sépare les pleins états des états vides, dans la manière propre à la température 0K et dans la manière moins graduellement définie avec l'augmentation de de la température.

11) densité de D(stateset) dans le cas d'unidimensionale :

Il caractérise le nombre d'états électroniques pour l'intervalle unitaire de l'énergie. On l'estime en observant cela à chaque nombre n de quantico là sont 4 états d'énergie disponibles (pour la symétrie de la parabole et le principe de l'exclusion de Pauli) donc mais étant 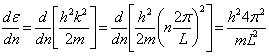quindi où dans dernier a été remplacé. Après que tout donc le diagramme de D(et) selon et est diminuer exponentiel, qui s'est multiplié pour la fonction de la distribution de ferme-Dirac il dit à nous que cela sous l'exponentiel les états sont seulement occupés pour et < et_{le F} .

 

12) circonférence de société :

C'est une circonférence du plan du k qu'il sépare les pleins états des états vides, dans la manière propre à la température 0K et dans la manière moins graduellement définie avec l'augmentation de de la température.

13) densité et société de sphère de D(stateset) dans le cas tridimensionnel :

C'est une sphère dans l'espace du k qu'il sépare les pleins états des états vides, dans la manière propre à la température 0K et dans la manière moins graduellement définie avec l'augmentation de de la température. _ raisonner comme dans le unidimensionale cas être trouver, ébauche un racine sous qui pour et < et_f là être le occuper énoncer.

 

14) explication en termes de gaz de la société de l'égalité entre les capacités thermiques aux isolateurs et les métaux :

En bref que le dilemme est qu'on ne le comprend pas comme, étant à nous beaucoup d'électrons, ils ne contribue pas à l'énergie de magasin, l'explication de celle dans la limite du gaz de la société est que les électrons sont fourrent très à vous et réglé du principe de Pauli donc ceux à vous à une plus petite énergie ne peuvent pas échanger l'énergie parce qu'elles ne doivent pas disposition être libres sur ce que pour se disloquer avec de la peu d'énergie qui vient à lui ont fourni pour la manière thermique. Le pourcentage des électrons qui peuvent acquérir l'énergie KT est donc le nombre d'électron qui peut acquérir l'énergie est et le total d'énergie est donc et d'elles les capacités thermiques sont seulement ébauche gagnée d'une valeur inférieure d'un cent concernant les capacités thermiques dues au fononi dans combien de T⁴ _F @10K.

Nous sommes donc en position à interpréter le cours les éprouve des capacités thermiques aux métaux affirmant qu'à de basses températures le cours linéaire qui a eu règne aux électrons tandis qu'aux températures élevées le cours cubique qui a eus règne au fononi.

 

15) explication en termes de gaz fermes de de l'ouvrier électrique de conductivité :

Ç$⪠que la loi de l'ohm dans la forme locale est , afin de gagner v_d s'applique à un champ électrique et, la force qui les actes sur l'électron est et pour 2ª la loi de la dynamique de laquelle il regarde cela est constante et donc il y a un mouvement rectiligne uniforme dans l'espace du k, à la présence des imperfections est en position au traslata le maintien la société de sphère après que soit déplacé la période dt de la quantité , puis a de quel et donc l'ouvrier électrique de conductivité est .