Diffraction des cristaux et du bonnet mutuel

1)    état de Bragg :

C'est la condition pour imposer à la longueur d'onde d'un incident d'annulation avec un angle q concernant l'axe X de sorte qu'il puisse donner l'endroit à l'interférence constructive si sended contre des plans réticulaires sépare de la distance d. le condizione à vous

il est caractériser obtenu immédiatement au-dessous du plan réticulaire, concevant le faisceau qui réfléchit là-dessus et estimant la longueur optique dans plus concernant la réflexion sur le plan surplombant. Affinchè les deux faisceaux ont lieu dans la phase sont nécessaire qu'une telle différence de la distance soit un n multiple de la longueur d'onde l.

 

2) Calcolo di Laue pour l'amplitude de la vague diffuse :

L'ébauche d'un calcul qui vient a présenté afin de limiter l'erreur de la base du calcul de Bragg, celui considère les plans réticulaires comme des miroirs se reflétants parfaitement et donc.

Un des points du bonnet comme l'origine est considéré ou, un point situé à une distance r de lui vient investi d'une vague plate que nous considérerons toujours chronométrer t = 0. Dans r est eu mais ce point devient source des vagues sphériques secondaires pour lesquelles l'amplitude de l'annulation sur l'endroit de détecteur à une distance r de r et R de l'origine il est où le Kr ils sont les modules parce que dans une vague sphérique les deux porteurs sont toujours des parallèles.

Nous écrivons à r en fonction des autres le grandezze et donc l'ha 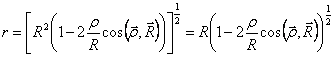où r< < R dans combien le cristal a des dimensions infinitésimales, puis se développer en série de tailleur a cela remplacé dans l'exponentiel donne à la limite et^l'ikR peut être négligé dans combien de constante sur tout le volume tout en étant le porteur dans avoir la direction qui l'origine avec les cartels de détecteur et car le module k a où Dk il est le porteur de la dispersion.

Naturellement le détecteur que les contributions des autres points du bonnet atteignent 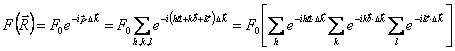également.

Si comme exemple dans le bonnet là sont des atomes de M et nous considérons premier seulement le récapitulatif est eus : 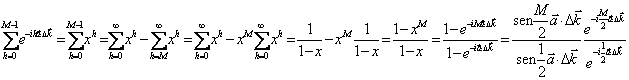là où j'ai rassemblé l'exponentiel avec la moitié de l'exposant.

Il vient mais a trouvé l'image de module de cette taille le maximum dont elle est obtenue décommandant le dénominateur pour lequel est et donc où q il est entier.

Analogue pour le sommaire d'autres trovano 2 .

Ce calcul est mais encore imparfait dans combien il ne juge pas le compte du multiple de dispersion.

 

3) états de Laue pour la diffraction maximum :

Ils sont gagnés du calcul précédent de Laue :

là où q, r, s est des nombres entiers.

 

4) porteurs de la traduction du bonnet mutuel :

là où le dénominateur représente le volume de la cellule du bonnet cristallin.

Leur expression a été construite de sorte qu'une celui qui ils combinaison linéaire satisfait les équations de Laue pour la diffraction maximum.

 

5) état de diffraction :

La diffraction est eue selon Laue quand le porteur de la dispersion s'avère être égal à un lesquels des porteurs de G du bonnet mutuel c'est-à-dire, ne doivent pas être nulle démontrée dans combien les porteurs de la traduction du bonnet mutuel , a été construits juste pour satisfaire les équations de Laue. Cette loi peut également être exprimée en divers allora de forme en fait , l'élévation à la place est eue mais soit une question elle-même de disperser l'élastique que c'est k eu^'= k et donc l'équation assume la forme qui est satisfaite si k il finit sur un plan normal à dans le point de moyens de .

 

6) relation entre le bonnet mutuel et le bonnet cristallin :

Chaque porteur du bonnet mutuel est orthogonal à un plan du bonnet cristallin.

Nous considérons le plan qui intersecte les as du bonnet cristallin dans les points , à lui appartenons les porteurs e . On le démontre que leur produit vectorial avec un porteur générique vaut la peine 0, obtiennent 3 équations qu'elles sont satisfaites pour , dans lesquelles regarde cela que les coefficients de G correspondent aux index de Miller du bonnet cristallin.

 

7) distance entre deux plans réticulaires :

Elle est donnée de la relation où h, k, l ils sont les index de Miller du plan à quel G il est orthogonal. De cette relation on déduit qu'à chaque point de la réflexion possible de bonnet mutuel du bonnet cristallin correspond on.

 

8) relations entre les lois de Bragg et celle-là de Laue :

On a les deux lois des équivalents 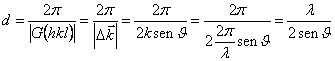en fait et donc qui est juste l'état de Bragg.

 

9) première zone de Brillouin :

Ébauche de la cellule de Wigner Seitz construite sur le bonnet mutuel.

 10) sphère d'Ewald :

Étant allora donc concevant à un porteur k que vous finissez dedans à l'n'importe quel point du bonnet mutuel et d'imaginer de le faire au ruotare pour créer un cercle ou une sphère, si un faisceau de diffratto intersecte un autre point du bonnet mutuel, vous vous formez, le porteur trouvé est orthogonal au plan du bonnet cristallin concernant lequel il y a réflexion.

 

11) facteur de structure géométrique :

La théorie de Laue est corrigée dans le chaque cas le point que réticulaire est formé d'un atome simple mais si les atomes sont plus d'un, un facteur de structure géométrique devra être considéré que le compte de la position de ces atomes à l'intérieur des prises unitaires de cellules ce facteur de correction vaut la peine où f_j il est le facteur de forme et c'est une mesure de la puissance de la dispersion du j-esimo d'atome dans la cellule unitaire.