Bandes d'énergie

1) évolution du modèle du gaz de la société :

Le modèle du gaz de la société néglige 2 phénomènes importants :

)       à raisonnable ? c'est un électron-électron d'interaction, il est des mises à niveau associées ils ignoto mais constante.

b)       Il est raisonnable qu'il y ait une interaction avec la ionienne du bonnet, est des mises à niveau associées elles périodiques dans l'analogie serrée avec la nature périodique avec quels atomes ils sont présenté dans le bonnet dans combien doit être le compte tenu que l'électron supporte une fortement répulsion d'une partie des noyaux dans la vertu du principe de l'exclusion de Pauli, puisque dans la correspondance des noyaux tous les états sont occupés.

 

2) équation de vague pour un électron dans les mises à niveau elles périodiques :

Nous considérons un bonnet linéaire en du lequel les atomes sont distance à vous à entre d'eux. Dans l'équation de Schroedinger ils sont remplacés :

)       la série de Fourier de yle (x) supplémentaire sur le simple k vous approuvez vous-même des conditions avec la découpe .

b)       la série de Fourier des mises à niveau elles u(x) périodique supplémentaire sur les porteurs de G du bonnet mutuel .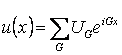

L'obtention à partir ce que qui a l'endroit K '= G K mais qui est un index sourd-muet peut également être risostituire avec du K donc plaçant d'elle a 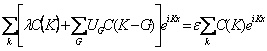l'uguagliando les coefficients des 2 séries et portant tous à 1° le membre est eu qui est ledit système des équations les centre.

 

3) théorème de bloc :

Il affirme que l'autofunzioni de l'équation de Schroedinger pour la mise à niveau elles périodiques ont la forme qui est sont le produit d'une vague plate pour la mise à niveau les ayant la même régularité du bonnet.

Nous avions assumé pour y(x) de la forme du type.

Du système des équations qu'ils centre des regards à celui le k permis pour la fonction de vague, ils ne sont pas continue mais ils sont de la forme où k est choisi pour enfermer entre le k est approuvé des conditions la découpe. Elle a elle-même : 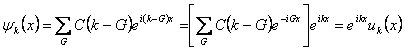là où c'est des mises à niveau ils périodiques depuis la série effectuée sur les porteurs du bonnet mutuel, est invariable pour la traduction de la même.

 

4) considérations sur l'impulsion pour l'électron du bloc :

Il vérification que la relation à la base de la théorie de Schroedinger en fait n'a pas elle-même : donc k n'est pas le moment de l'électron du bloc et ne vient pas donc presque appelé moment ou moment cristallin.

 

5) le modèle de presque libèrent des électrons :

Vu 2 équations tirées du système des équations les centre qu'elles diffèrent seulement pourun porteur G ₁ du bonnet mutuel, ha est noté qu'il y a relatif le récapitulatif à l'énergie les améliore parce que dans le modèle de presque libérez les électrons on le suppose que que l'énergie cinétique est beaucoup la plus grande de l'énergie les améliore, nous pourrait la négliger complètement mais nous tenons 2 limites afin de faciliter les calculs, suppose que d'ailleurs que la fonction égale les améliore périodiques est on donc . On trouve le système précédent a les solutions simples si de détermination est 0, qui les racines sont , à ce point s'il est choisi pendant que l'index de l'autofunzioni coïncide avec le bord de 1ª la zone, obtient et donc e . Remplaçant dans les équations de départ est déterminé et et d'elles le y qu'elles s'avèrent être 2 vagues se tenantes une du type type cosinus pour lequel a que la densité de la probabilité pour trouver des électrons est maximum dans la correspondance de la ionienne positi à vous et donc elle diminue l'énergie, alors que l'autre est de type sein et la densité de la probabilité pour trouver des électrons est maximum entre deux ceux ioniens est donc la solution à une énergie plus élevée.

 

6) espace d'énergie :

C'est la bande des énergies interdites qu'il jaillit de l'équation de l'électron du bloc. Nous avons puisque sur le bord de zone e est eu donc l'espace vaut la peine 2u₁ . Vous vous notez que cela dans le modèle du gaz ferme de u₁ = 0 et donc l'espace pas est et une parabole continue est eue.

 

7) nombre d'états dans une bande :

Nous avons eu déjà puisque s'appliquant les conditions à la découpe de Karmann un constate que le n° de compatible de k contenu dans 1ª la zone il est l'égale juste N qui est au nombre d'atome duquel la chaîne linéaire se compose, mais les électrons sont des fermions donc que nous peuvent être 2 électrons avec du même k mais tourner l'opposé, donc à l'intérieur de 1ª la zone 2N ils ont été disponibles.

 

8) détermination des métaux avec la théorie des bandes :

Chacun des atomes de N d'un métal peut fournir un électron qui au total sera N et donc ils peuvent seulement remplir la moitié de 1ª que la bande composée de 2N soit libre, ces électrons sont donc libre pour absorber l'énergie et pour passer aux états à l'énergie élevée plus. D'une façon généralisée toute sont les métaux les atomes avec la valence un nombre inégal d'électron.

 

9) détermination des isolateurs avec la théorie des bandes :

Chacun des atomes de N d'un isolateur peut fournir deux électrons qui au total seront 2N et donc ils remplissent complètement 1ª que la bande composée à partir de 2N soit libre, puisque les états libres sont séparés à vous du dessus de la pleine bande élevée d'un espace, ces électrons ne peuvent pas absorber donc pour transporter l'énergie. D'une façon généralisée toute sont les isolateurs les atomes avec un n° égal des électrons de valence.

 

10) détermination des semi-conducteurs avec la théorie des bandes :

Les atomes de semi-conducteur de N a la valence moyenne 4 donc au total est les atomes 4N et donc les 2 premières bandes seront complètement pleines comme pour un isolateur, duquel mais d'elles distinguez dans combien l'espace entre le 2ª et le 3ª la bande coûte beaucoup petit, donc déjà aux électrons ambiants de la température dans la bande de conduction sont eus.

 

11) contour de la zone réduite :

C'est un procédé qui consiste en fabrication que le porteur index cristallin du moment k de la fonction du bloc appartient à 1ª la zone de Brillouin, cela qu'il est toujours possible ajoutant un porteur opportun de G du bonnet mutuel.

 

12) contour de la zone répétée :

Elle est obtenue répétant l'espace le long de l'axe du k, combien a été obtenu pour le k de 1ª la zone, une est obtenue en tels fonction de manière et_K périodique.

 

13) contour de la zone étendue :

On l'a que pour chaque zone il vient rapporté la valeur corrigée de l'énergie des états disponibles, sans celui doit comprimer toute à l'intérieur de 1ª la zone.

 

14) comme concevoir la surface de la société pour les électrons libres :

Ils conçoivent 1ª, 2ª, 3ª la zone avec le procédé de Wiegner Seitz, considère alors la circonférence de la société qui contient 1ª la zone entière, parce que l'autre répartit en zones autre n'est pas faite à cela pour caractériser l'intersection avec la circonférence de la société et du traslare ces secteurs à l'intérieur de 1ª la zone de sorte qu'ils créent avec relié.

 

15) comme concevoir la surface de la société pour presque librement des électrons :

La surface de la société est gagnée avant pour les électrons libres et alors il est nécessaire de tenir le compte qu'au bord de zone le v_g il est décommandé et donc le gradient de l'énergie concernant k vaut la peine 0 qui est nous ne peut pas être des discontinuités, n'est pas donc nécessaire de mat les angles.

 

16) effet d'un champ électrique et sur l'électron du bloc :

S'appliquant à un champdans une direction, l'intégration est donc des augmentations eues de k du temps dans la direction opposée à jusque 2'à celle, atteint sur le bord de zone qu'il supporte Umklapp et le ricompare de l'autre côté de 1ª la zone qui est avec du k un négatif, est qui est venu pour créer un courant alternatif, que dans le fondamentamente de vérification de vérité pas pour la présence de deux causes qui rendent améliorez-les non périodiques à l'effet contraire de combien sont affirmés dans l'hypothèse du bloc :

)       les imperfections dans le bonnet aiment des lacunes ou l'impurità.

b)       à 0K le bonnet il est seulement ferme tandis qu'aux plus grandes températures, le bonnet est dans la vibration et à la moyenne la régularité du même bonnet est seulement eue.

 

17) mouvement d'un électron en présence d'un champ magnétique :

Les électrons couvrent les lignes de la société ont en fait et du repos donc la force est toujours orthogonale au mais elle est orthogonale à la superficielle à l'énergie constante car exactement les lignes de la société selon lesquelles après tout le mouvement de l'électron est effectué. Au deuxième au sujet de la distance en arrière l'électron est parlé au sujet de l'orbite du type ou du type espace. Le type orbites sont espace eu quand le dessus d'une pleine bande possède des états vides.

 

18) lacunes :

La détention restante que les seuls porteurs de la charge est les électrons et a le négatif de charges, l'hypothèse de leur existence est beaucoup de bénéfice afin d'expliquer la situation suivante :

Il y a une bande complètement pleine à moins qu'on soit libre (espace) dans le dessus à lui, appliquant un champ et_z dans la direction du k l'augmentant est eu que les électrons (..e implicitement l'espace) sont déplacés sur être gauche . Vu un moment successif à l'application du champ on l'a que l'espace a été déplacé, et sa vitesse est augmentée (..corrisponde à la tangente à la bande). Un tel résultat peut être motivé ou assignant à l'espace qu'il charge le négatif et une masse négative, ou d'accord à la mécanique classique, à une masse positive et aux charges positives.

 

19) seconde loi de dynamique pour les électrons libres :

La partie de la détermination du travail accompli du champ et sur un électron dans le temps dt d'ailleurs et donc l'uguagliando le det a donc est apparemment 2ª respecté la loi de la dynamique, apparemment en combien k ne coûte pas l'impulsion de l'électron du bloc puisqu'il ne respecte pas .

 

20) la masse efficace :

C'est une mesure de l'inertie qu'un électron de bloc présente quand à elle une force externe est appliquée, est la dérivation gagnée concernant le temps où le v_g a : _ et donc être avoir où m^* être le efficace masse qui donc être inverse proporziona les le courber le courbe dispersion dans le espace le k, en particulier dans correspondance le zone bord le courber être négatif donc être aussi le efficace masse, qui vouloir pour dire cela appliquer un force diriger vers le zone bord, le mouvement produire dans opposé sens, qui produire pour par l'intermédiaire le réflexion le Bragg. De manière analogue si elle est approchée à nous le bord de la zone de la bande avançée que courber est positif et avec elle la masse efficace, cela elle est petite est donc comme si un effet de recul facilite l'électron pour aller loin à partir du bord de zone.

 

21) Resistività d'un métal :

Le resistività r d'un métal est fonction est de la température qui des imperfections du bonnet, est en particulier de chargeing à ce dernier resistività résiduel r₀ qui est eu également quand la température descend à 0 K. On l'a que les feuilles de resistività de la valeur r₀ se développe comme T⁵ pour T < < q_D dans l'ordre puis à se développer comme T aux températures T < < q_D .

Il est important cependant de noter que pour un métal le resistività devient la croissance de la température tandis que pour un semi-conducteur le resistività diminue à la croissance de la température.

 

22) explication du cours linéaire du resistività aux températures élevées :

Il est nécessaire de faire la référence à la sphère de traslata de la société et aux modalités afin de la lui rapporter en position les commence une fois que le champ électrique n'agit pas plus. Le resistività augmente pour par l'intermédiaire de des coups du type d'Umklapp du fononi avec des électrons, le fononi utile elles sont ceux avec du k semblable à k_{le Debye} et leur nombre augmente linéairement avec la température et lui le resistività.

 

23) explication du cours du type T⁵ du resistività en fonction de la température :

Avec diminuer de la température, on l'observe de la fonction de Bose-Einstein que le nombre du fononi capable donner l'endroit aux coups du type d'Umklapp diminue de la manière exponentielle, mais devient le nombre du fononi signicatif cela en raison d'arrivé à vous frappe avec du k plus petit réussissent pour obtenir le même résultat.