Propriété des systèmes dans l'espace d'état
1) norme d'une matrice :
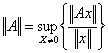
étant défini en termes de norme de x évidente que divers elle est choisie pour ||X|| ils impliquent différentes normes de à.
2) l'équilibre d'un système des équations les différencie :
Le supposer que le système 
admet la
solution banale X = 0 ceci vient assumé comme équilibre et est
supposé que que le point relatif d'Al de solution les commence x0 existe autour dans un son.
3) équilibre stable :
L'équilibre serait stable si pour le chaque et > 0 un d existe > 0 tels que 
chaque pour le ³t0de t et à condition
que ||X0|| < d . En
bref on l'a que si le point les commence x0 il est contenu dans un ipersphere de faisceau centré d dans t0 alors est eu que la solution du
système des équations les différencie les restes confinés dans un
ipercilindro de faisceau et autour
de l'axe t qui implique que si l'équilibre est stable dans la
correspondance pour chronométrer le t=t0 est alors stable dans la correspondance à celui qui 0 fois les commencent t 1>t aussi pour choisir valeur opportune pour d.
4) équilibre attrayant :
L'équilibre s'avère être attrayant s'il existe h> 0 tels qu'ha 
pour
le chaque ||X0|| < h .
5) asymptotiquement équilibre stable :
L'équilibre est dit qu'asymptotiquement l'écurie si elle est en même temps est stable qu'attrayante.
6) asymptotiquement équilibre stable total :
Ébauche du cas dans lequel pendant que la valeur les commence elle prend un divers point de l'origine.
7) équilibre instable :
L'équilibre de l'équation les différencie est instable s'il n'est pas stable.
8) états d'équilibre pour un système linéaire et stationnaire :
On observe la solution de l'équation d'état dans le cas
stationnaire 
considère au commencement l'absence de
forcer 
le quindi que la solution est combinaison
linéaire 
des limites où l est l'autovalore de la matrice de dynamique et du r
sa variété, est eue donc que l'équilibre est asymptotiquement
écurie si toutes les racines de la caractéristique polynôme de la
matrice pour avoir la vraie partie négative, si également simple
d'elles est à la vraie partie positive, l'équilibre est instable.
Dans le cas à la place que les variétés 1 ont des racines pour annuler la vraie partie alors, relativement elles, le système est stable mais pas asymptotiquement écurie tandis que le système est instable si les racines pour annuler la vraie partie ont une plus grande variété d'une.
Considérant également la réponse obligatoire, on l'a
que le système s'avère l'écurie si tout l'autovalori de la matrice
de dynamique sont à la vraie partie négative et forcer est limité
en fait 
.
9) état controlable :
Un état serait controlable dans la correspondance à un
moment t>0 si une fonction d'un tel revenu permis existe u qui
est eu l'espace des états controlable
est indiqué avec Xc.
10) Matrix de la contrôlabilité :
elle concourt pour caractériser exactement à l'intérieur de l'espace de l'état que le sottospazio des états controlable a déterminé à partir de l'image de cette matrice.
11) principe fondamental caractéristique de avec des états controlable :
Avec des états controlable il ne dépend pas du temps t, ceci seulement de la manière théorique dans combien pour un vrai système physique, pour passer d'un ne coûte pas nul à un soit nul dans un temps arbitraire pourrait exiger un revenu tellement large pour introduire la saturation un certain élément du système.
12) système controlable :
C'est un système pour lequel avec des états controlable il coïncide avec l'espace d'état, celui se produit si la matrice de contrôlabilité a le rang de maximum, qui est est inversible.
13) système raggiungibile :
Un système serait raggiungibile si supposer que l'état les commence est la nulle x(0) = 0, peut être fait de la manière de rattraper un temps final déterminé td'Al de l'état X f étant appliqué un revenu opportun entre 0 et t.
14) forme de Kalman pour la contrôlabilité :
Si le grade de la matrice de contrôlabilité n'est pas maximum, et donc l'espace des états controlable est plus petit de l'espace d'état, il est nécessaire de choisir car la base pour l'espace d'état une base dont le premier les porteurs restants sont une base pour l'espace des états controlable et des porteurs est n'importe quel purchè dans le nombre opportun.
Dans la nouvelle base le système est décrit des matrices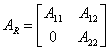 
; 
; 
,
d'ailleurs le porteur d'état peut être partizionato dans le parent 
par porteur aux états controlable et le vettore 
a relativement aux états non controlable, les
équations d'état peut facilement être estrinsecare et elles pour
déduire le contour équivalent aux blocs. La fonction de
transfert qui gagne 
est relativement au
sous-ensemble controlable décrit donne seulementà 11 , b1 , c1 .
15) forme de la Jordanie pour la contrôlabilité :
Si la matrice de dynamique à est diagonalizzabile, alors le système est controlable à condition que les membres du porteur du revenu transformé dans la nouvelle base sont tout le non nuls. Si à la place il n'est pas diagonalizzabile, alors il est nécessaire de la transformer dans la forme canonique de la Jordanie et l'état de contrôlabilité est que les membres du porteur du revenu transformé b les correspondants aux dernières lignes des blocs de la Jordanie qui constituent la matrice transformée ne sont pas nuls.
16) état indistinguible de l'état 0 :
Un état X est indistinguible de l'état 0 dans
l'intervalle (0,t) s'il vaut la peine le escroc 
de
relation 
, celui est si à l'état correspond une
réponse dans l'évolution libre nulle dans l'intervalle (0,t).
17) états non observables :
Un état n'est pas observable s'il est indistinguible de l'état 0. L'espace des états non observables est indiqué avec Xpas.
18) Matrix d'osservabilità :
C'est la matr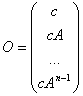ice 
, il concourt pour
caractériser exactement à l'intérieur de l'espace de l'état que le
sottospazio des états non observables a déterminé à partir du
noyau de cette matrice.
19) système observable :
Un système est observable si avec des états non observables qu'il a la dimension nulle donc n'existent pas soit l'inosservabili divers de zéro, celui se produit si la matrice d'osservabilità a le grade de maximum qui est le noyau (…ce il caractérise les états non observables) coïncide avec avec vide.
20) forme de Kalman pour l'osservabilità :
Si le noyau de la matrice d'osservabilità n'a pas la dimension nulle, est nécessaire pour choisir car la base pour l'espace de l'état restant une base dont les premiers porteurs sont une base pour l'espace des états non observables et des porteurs est n'importe quel purchè dans le nombre opportun. Dans la nouvelle base le système est décrit des matrices :
;
;
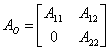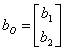d'ailleurs le porteur d'état peut être partizionato dans
le parent 
par porteur aux états non observables et
parent que 
un porteur à la chose observable
énonce, les équations d'état peuvent facilement être estrinsecare et elles pour déduire le contour équivalent aux
blocs. La fonction de transfert qui gagne 
est
relativement au sous-ensemble observable décrit donne seulementà 22 , b2 , c2 .
21) forme de la Jordanie pour l'osservabilità :
Si la matrice de dynamique à est diagonalizzabile, alors le système est observable à condition que les membres du porteur de l'évasion transformé dans la nouvelle base sont tout le non nuls. Si à la place il n'est pas diagonalizzabile, alors il est nécessaire de la transformer dans la forme canonique de la Jordanie et l'état d'osservabilità est que les membres du porteur transformé des correspondants de l'évasionc j aux premières lignes des blocs de la Jordanie qui constituent la matrice transformée ne sont pas nuls.
22) décomposition canonique de Kalman :
Il est nécessaire de déterminer 4 bases :
) B1 est une base pour les états controlable et non observables
b) B2 est un accomplissement de B1 à une base pour l'espace des états controlable
c) B3 est un accomplissement de B1 à une base pour l'espace des états non observables
d) B4 un accomplissement est-il de B1 ? B2 ? Basede B 3 à un d'"4
dans la base de "n qu'il obtient le giustapponendo les porteurs des bases précédentes, le système est décrit des matrices :
;
;
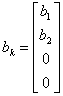d'ailleurs le porteur d'état peut être partizionato dans :
un porteur X1(t) a rapporté le système au controlable
un porteur X2(t) a rapporté le système à la chose observable controlable de e
un porteur X3(t) a fait rapport au système non controlable e non observable
un porteur X4(t) a fait rapport à la chose observable non controlable du système e
Un résultat important est que la fonction de
transfert qui gagne est relative seulement au
sous-ensemble controlable et observable.
23) l'affinchè de condition un système est observable et controlable :
Il doit écrire dans la forme minimale qui est la fonction de transfert ne doit pas avoir des annulations.
24) annulations légales :
Une annulation est ledit légale si la manière associée à elle est stable.
25) réalisation :
Les moyens du s le passage de la représentation au moyen de la fonction du transfert à celui-là dans l'espace d'état.
26) réalisation dans la forme canonique du contrôleur :
Ébauche du passage de la fonction du transfert à la matrice de contrôlabilité.
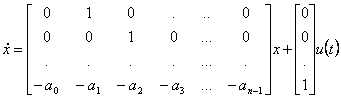
là où b0 …bm sont les coefficients de I du numérateur de la fonction du transfert età 0 …à n-1 sont les coefficients du dénominateur de monico de le même. La matrice de la contrôlabilité de ce système s'avère indépendamment être du rang maximum du fait qui nous a été ou les petites annulations et donc le système est controlable sûr.
27) réalisation dans la forme canonique de l'observateur :
Ébauche du passage de la fonction du transfert à la matrice d'osservabilità
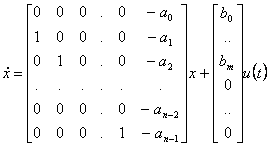
là où b0 …bm sont les coefficients de I du numérateur de la fonction du transfert età 0 …à n-1 sont les coefficients du dénominateur de monico de le même. La matrice de l'osservabilità de ce système s'avère indépendamment être du rang maximum du fait qui nous a été ou les petites annulations et donc le système est chose observable sûre.
28) réalisation dans la forme canonique de la Jordanie :
Ébauche du passage de la fonction du transfert à la forme de la Jordanie, il est particulièrement utile dans le cas que le dénominateur de la fonction de transfert est fattorizzabile facile, et donc la résiduelle peut être calculée, peut être installée le problème de deux diverses manières obtenant seulement l'alerte à vous égale pour cela qu'elle considère la matrice de dynamique à.
Comme exemple considérant un poteau triple et deux poteaux simples les équations d'état d'associé sont :
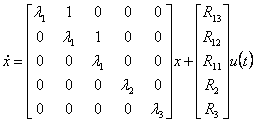
