L'endroit des racines

1) endroit des racines :

Il est un technique que concourt pour représenter graphiquement les effets du passage du cycle ouvert, en bref est eu qu'à changer du gain k les poteaux sont déplacé d'une telle manière déterminant la stabilité ou l'instabilité du système, d'ailleurs de vrais poteaux ouvrir le cycle qu'elles peuvent également être créées des conjugés complexes de poteaux à vous a fermé le cycle qui si le système est stable détermine un en raison amorti par réponse d'oscillation de x et de W_i que dans les listes détaillées il vient exigé de l'entité légère.

2) système à la stabilité régulière :

C'est un système qui s'avère l'écurie pour un intervalle du gain comporté k entre 0 et une limite avancée par valeur k_Lqui peut coïncider avec le ¥ , un tel gain caractérise les courrier de poteaux sur l'axe imaginaire. Il est parlé au sujet du système à la stabilité paradoxale dans combien qui augmente le và gagnez vers la stabilité.

3) système à la stabilité conditionnée :

C'est un système qui est stable si le gain est contenu dans un intervalle du gain comporté k entre deux valeurs finies.

4) système à la stabilité paradoxale :

C'est un système qui s'avère stbile pour un intervalle du gain comporté entre une limite finie par valeur k_L et le ¥.

5) endroit positif :

En outre l'endroit des racines est dit et correspond dans la position des racines de l'équation caractéristique de la fonction du transfert du système de boucle bloquée pour un gain k > 0.

6) endroit complémentaire :

En outre l'endroit est ledit négatif et correspond dans la position des racines de l'équation caractéristique de la fonction du transfert du système de boucle bloquée pour un gain k < 0. Il est important pour l'étude des systèmes pour la rétroaction positive, et dans le cas dans lequel un système qu'elle est stable pour des valeurs vous a seulement nié de k.

7) relation fondamentale pour la construction de l'endroit des racines :

Être lui est eu que l'équation caractéristique est vérifiée si cette condition implique un sur les modules et une condition dessus est faite.

8) état des modules :

La relation fondamentale est vérifiée jusque les modules si le module du trasferenza pour ouvrir le cycle est , cette condition ne concourt pas pour tracer l'endroit dans combien pour chaque k est satisfait des points d'infinites du plan, cependant une fois que l'endroit a été tracé par la condition sur les modules il concourt pour la recevoir un diplôme en k en fait pour chaque point s que concerner l'endroit peut être gagné le k pour l'associer quel rapport entre le produttoria des longueurs des porteurs qui combinent les poteaux du F(s) avec s et le produttoria des longueurs des porteurs qui combinent les zéros du F(s) avec squi est .

9) la condition de est faite :

La relation fondamentale est vérifiée jusque des marques si la phase du trasferenza pour ouvrir être entier positif de è de F(s) de cycle r ou nul. En bref par point s du plan complexe appartient à l'endroit positif si la somme des angles concernant le plan horizontal des porteurs tracés des zéros et des poteaux du F(s) vers le point s est nombre impair multiple ±de 180°. Dans pratique c'est r=0 utilisé et pour k>0 il est pris moins.

10) branche de l'endroit complet des racines :

C'est l'endroit des points du plan complexe couvert d'une des racines de l'équation caractéristique quand k qu'il change entre -¥ et ¥ .

11) nombre de cuivre de l'endroit des racines :

Le nombre de cuivre est égal à plus grand entre le nombre de poteaux n et le nombre des zéros m de la fonction du transfert au cycle ouvert F(s).

12) points de l'endroit des correspondants de racines à k = 0 :

Ils sont les poteaux du F(s) en fait , remplaçant k=0 est obtenus .

13) points de l'endroit des correspondants de racines à k = ±¥ :

Ils sont les zéros du F(s) en fait de la condition sur les modules a en fait pour le ¥®de k a 0 à 2° le membre et donc afin de vérifier les 0 égalités NumF(s) doit être également qu'elle se produit si nous nous trouvons dans les zéros du F(s).

14) Simmetrie de l'endroit complet des racines :

Une symétrie concernant le vrai axe est eue toujours en fait l'équation caractéristique est à de vrais coefficients donc que ses racines est vraie ou aux croisillons complexes conjugués. Simmetrie des poteaux sont possible également et respect de zéros à d'autres as qui doivent nécessairement être verticaux dans combien obtiennent vrai axe pour vallon géométrique de transformations le 'qui doit mais respecter toujours le respect de symétrie à un croisillon des poteaux.

15) nombre de cuivre avec lequel l'endroit positif diverge à l'angle infini et relatif :

L'endroit positif diverge à infini avec |n-m| cuivre, l'angle vaut la peine , avec le positif entier de r donc si un système présente une égale les poteau-zéros qu'excessifs à 0 n'a pas le sens le schematizzazione du 0 à l'infini. On déduit de la condition dessus est fait observer cela quand le point va à l'infini tous les porteurs qui le combinent avec des poteaux et les zéros sont des parallèles ont donc la même phase. On l'observe que les asymptotes caractérisent donc ne vous font pas la partie de l'endroit et ne sont pas donc cuivre de l'endroit positif que ceux du négatif d'endroit peuvent intersecter les mêmes asymptotes.

16) Barycentre de l'endroit et des formules afin de le caractériser :

Ébauche du point du vrai axe qui s'avère être intersection des 2|n-m| des asymptotes, dans les systèmes de boucle bloquée il s'avère être invariable à changer de k, est caractérisé de la formule 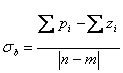que le pu² pour se simplifier vous considérant le soleil laissent vraie puisque les poteaux et les zéros sont conjugé complexe à vous et donc l'elidono de pièces imaginaires.

17) états des affaires de l'endroit positif au vrai axe :

Tous les points du vrai axe appartiennent à l'endroit positif qui laissent à leur droite un nombre tout à fait inégal de vrais poteaux et de vrais zéros de la fonction du transfert au cycle ouvert, compte chacun à vous avec la variété respective. On le démontre au congé d'une condition dessus est fait observer cela le porteur qui combine un poteau avec un point s correspond une contribution dans la phase de -180° si le poteau est trouvé vers la droite ou de 0° si le poteau est trouvé du côté gauche du point s, alors que si vers la droite du point s un zéro sont trouvés, la contribution dans la phase est de 180°.

18) angle du départ à un poteau :

C'est l'angle auquel la branche de l'endroit positif est assortie loin du poteau, il est donné de la relation suivante :

19) angle d'arrivée dans un zéro :

C'est l'angle avec lequel la branche de l'endroit positif arrive dans les zéros du F(s) va loin du poteau, il est donnée de la relation suivante :

20) comme caractériser les points d'intersection de l'endroit des racines avec l'axe imaginaire :

Il doit être appliqué au critère de Routh caractérisant donc le k pour lequel le système est à la limite de stabilité et donc les poteaux sont sur l'axe imaginaire, remplaçant cette valeur de k dans l'équation caractéristique que les valeurs de W sont obtenues .

21) points de singulier de l'endroit des racines :

On pique des points qu'ils représentent les racines multiples de l'équation caractéristique, cela est qui appartiennent en même temps cuivre davantage de l'endroit. À l'endroit complet des racines ils appartiennent davantage à n m-1 que le singulier se dirige.

Le singulier se dirige dans ce qui sont rassemblement simple distingué cuivrent concerner le même endroit et les points singuliers multiples dans lesquels le rassemblement concernant cuivre sont à l'endroit positif qui au négatif d'endroit, de tels points sont individualiste exclusivement dans les poteaux multiples ou mettent des multiples à zéro de la fonction du transfert au cycle ouvert F(s).

22) relation afin de caractériser les points de singulier :

_ l'uguagliando à zéro le dérivé de la trouvaille caractéristique d'équation le singulier de point qu'au but appartenir à l'endroit doit également satisfaire le nombre d'ébauche de La de La complexe et donc pour être de solution difficile, dans son vece peut employer 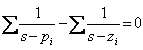que ne pas caractériser le multiple singulier de point, mais ceci obtiennent immédiatement en combien coïncident avec le poteau multiple et le multiple de zéros de la fonction du transfert au cycle F(s) ouvert. En outre pour cette équation la trouvaille de points à vous doit alors satisfaire .

23) la relation entre la variété et cuivre entrer dans le point singulier :

Si m sont la variété dont est le nombre cuivre présenter dans le point puis ces derniers qu'elles divisent le plan dans des domainesde 2 m d'amplitude égale.

24) nombre de points singuliers entre un poteau et un ceux contigu zéro :

Il y a toujours un numéro égal (0) des points singuliers entre un poteau et un ceux contigu zéro.

25) nombre contigu des points singuliers entre 2 poteaux ou deux zéros :

Il y a toujours un numéro inégal (1) des points singuliers entre un poteau et un ceux contigu zéro.

26) vers des flèches dans l'endroit positif et le négatif d'endroit :

D'une façon généralisée les flèches sont dans le sens du k augmentant -le ¥ un ¥ donc dans le négatif d'endroit les flèches vont des zéros (-du ¥) aux poteaux (0), alors que dans l'endroit positif elles vont des poteaux (0) aux zéros ( ¥).

27) analogie hydraulique :

Pour l'endroit positif les poteaux aiment les sources que donc le rejet cuivre de l'endroit et les zéros comme des piscines peuvent être considérées qu'attirez donc cuivre de l'endroit.

28) conditionne sur le système pour ouvrir l'affinchè de cycle que le système de boucle bloquée est écurie sûre :

Les poteaux et les zéros pour ouvrir la trouvaille toute de cycle dans le semiplan gauche, le barycentre est dans le vrai axe d'axe négatif et le nombre d'asymptotes est plus petit ou pour égaler plus à deux.

Fini retarde

29) quand il est nécessaire de se tenir le compte du retarde fini dans les vrais systèmes :

Quand l'ordre de grandeur du retarder s'avère plus grand de la plus grande constante que la période du système.

30) l'équation caractéristique en présence de fini retarde :

Du on l'a que les poteaux sont caractérisent à vous de l'équation caractéristique

31) des conditions sur les modules et dessus sont faites :

À partir du ricava caractéristique d'équation et donc elles obtiennent la condition sur les modules et la condition sur le fasi .

32) le nombre de cuivre de l'endroit :

Le nombre de cuivre de l'endroit est être infini infini le nombre de solutions de l'équation caractéristique importante.

33) typologie des points de l'endroit complet des racines pour lesquelles c'est k=0 eu :

De la condition sur les modules on regarde cela 2° que le membre est infiniment donc l'égalité est si nous nous trouvons dans les poteaux du F(s) ou du s = - ¥vérifié .

34) typologie des points de l'endroit complet des racines pour lesquelles le ¥ est eu k ±= :

De la condition sur les modules on regarde cela 2° que le membre est donc l'égalité nulle est vérifié si nous nous trouvons dans les zéros du F(s) ou du s = du ¥ .

35) Simmetrie de l'endroit complet des racines :

La symétrie concernant le vrai axe dans combien coûte se développer eu en série de tailleur obtient un algebrico polynôme.

36) l'application du critère de Routh dans le cas de fini retarde :

L'équation caractéristique ne peut pas être appliquée dans combien coûte importante a donc les solutions infinies, les intersections avec l'axe imaginaire peut être déterminée de la manière rapprochée avec un développement de la série coupée de l'exponentiel.

37) asymptotes de l'endroit complet :

Les asymptotes sont des infinites et sont tous les parallèles à l'axe des abscissas et ils l'intersectent dans la correspondance aux points .

38) relation entre k des infinites les endroits à l'intersection avec l'axe imaginaire :

On l'a que k que le correspondant à la branche qui intersecte l'axe imaginaire avec l'ancien plus petit est inférieur au k des cuivre qui intersectent l'axe imaginaire avec plus grand ancien.

39) concernant des considérations le tracciamento rapproché au moyen de développement en série :

Si l'exponentiel est développé en série, autre n'est pas fait à cela à ajouter des zéros dont le type (vrai ou complexe) et numérotez-lui dépend de l'ordre du développement auquel est arrêté à nous, regarde en particulier cela si est arrêté à nous à un ordre inégal il a vrai zéro qui détermine un endroit que le signe de la limite de l'ordre inégal de la puissance élevée n'est pas compatible avec les asymptotes horizontaux d'ailleurs que plus impose que pour échanger l'endroit positif avec le négatif. Le nombre de zéros présentés d'ailleurs se développe avec l'ordre du développement est donc nécessaire pour s'arrêter à un ordre 2 ou 4 au maximum, aussi parce que pour des puissances égales avançées des croisillons des zéros à la vraie partie négative sont eus.

40) approximation de Padè :

Fratta concourt pour rapprocher un polynôme avec une fonction les rationne, choisissant le degré du numérateur égal au degré du dénominateur est trouvé pour l'approximation de l'ordre 1° de l'exponentiel 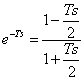tandis que pour l'approximation de 2° l'ordre 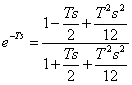célèbre cela dans les les deux les caisses obtient l'important avéré pour laisser les poteau-zéros excessifs mais dans le cas de l'approximation de 1° l'immutato d'ordre il est nécessaire pour échanger l'endroit positif avec le négatif d'endroit.

41) les considérations sur la stabilité dans le cas des systèmes à fini retarde :

On a l'ébauche des systèmes toujours instables, dans combien coûte présent des zéros équivalents qui sont trouvés dans le semiplan positif et puisqu'à la croissance de k l'endroit il est déplacé des poteaux au cycle ouvert vers les zéros au cycle ouvert, qui nécessairement và vers l'instabilité.

42) relation entre les poteaux pour ouvrir le cycle et les poteaux :

Une règle valide pour des systèmes avec le ³ 2 de n-m affirme que la somme de la position des poteaux pour ouvrir le cycle est égale à la somme de la position des poteaux.

43) découpe des racines :

En cas dans lequel dans un système là-bas au gain un autre paramètre comme la position à d'un poteau peut changer également, l'équation caractéristique factice obtenue fixant k (l'égale à 1 est écrite normalement) et rassemblant les limites dedans à , on l'obtient donc à partir derrière de ce qu'il peut être changé et trouvant l'endroit correspondant des racines.