L'analyse dans l'espace d'état

1) variable d'état :

Ils sont les variables qui doivent être créés quand une équation est eue les différencie de l'ordre n et elle est voulue être réduite à un système des équations de n les différencie du degré 1°, ébauche donc de l'intermédiaire variable que pas nécessairement elles correspondent aux largenesses mesurables physiquement cependant concourent davantage une description du soin pris du système concernant la fonction de transfert. Ils constituent un porteur d'état si la valeur de l'évasion dans un moment peut être obtenue

t > t₀célèbre qui est la valeur de toute la variable de l'état pour chronométrer t₀ et la valeur des revenus u au ³ t ₀ du tempst .

 

2) la comparaison entre l'approche au moyen de variable d'état et l'approche au moyen du transfert fonctionnent :

L'approche au moyen de la fonction de transfert est valide choisissent dans le cas du preferibilmente linéaire et stationnaire de système à un revenu simple et à une évasion variable simple alors que l'approche au moyen de d'état d'installation étant dans le dominion du temps, n'a pas ces limitations.

3) Spazio d'état :

C'est l'espace dans lequel les membres du porteur d'état sont les as coordonnent à vous.

4) trajectoire d'état :

C'est la distance décrite, dans l'espace de l'état, de l'extrémité libre du porteur de l'état à changer du temps.

 

5) équations dynamiques pour un système MIMO :

Un système MIMO possède de divers revenus et de diverses évasions sont décrites de la colombe de système :

À elle est la matrice du système, ou la matrice de dynamique

B est la matrice du revenu au système, ou matrice de forcer

C est la matrice de l'évasion du système

D est la matrice du revenu sorti par ouverture directe, dans les vrais systèmes qu'elle est nulle

u est le porteur de revenu

y est le porteur d'évasion

X est le porteur d'état

 

6) équations d'état pour un système SISO :

Un système SISO possède un revenu simple et une évasion simple, est décrit du système où le stavolta b, u et c est des porteurs et des matrices comme n'ont pas été eues dans les systèmes MIMO.

 

7) les équations d'état du moteur dans le continuum commandé circulent sur l'armure :

Observant les équations , , on l'observe que les seuls largenesses dérivés sont_{m que}le (t) eed W_m(t) sont donc prêtent bien pour constituer le porteur de l'état, du repos d'ailleurs le variable de revenu d'un moteur dans l'écoulement de continuum de Fédéral sur l'armure est senz 'autre la tension de l'alimentation de l'armure et_à(t) tandis que le variable de l'évasion est senz 'l'autre vitesse angulaire W_m(t). Localisant dans le premier membre de 4ª l'équation et remplaçant dans elle le 2ª et également localisant dans 1° le membre de 3ª l'équation et le sostiutendo dans lui le 1ª il est atteinte les équations d'état suivantes 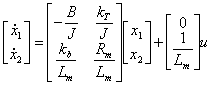où x₁ = W_m X₂ = I_m u = et_à y = W_m .

 

8) Matrix de la transition de l'état dans le cas du revenu nul :

C'est une matrice qu'en vigueur de l'absence concourt pour passer du porteur de l'état au temps 0 au porteur de l'état à la son expression du temps t c'est-à-dire, est la résolution obtenue au moyen de Laplace que l'équation la différencie et puis l'antitrasformandola, est eu en fait et donc quel antitransforming est eu et a donc que la matrice de la transition de l'état est . Il peut démontrer qu'il est esprimibile également dans la forme d'exponentiel de la matrice .

 

9) propriété de l'exponentiel de la matrice :

à)                  

b)                 

c)                  

 

10) propriété de la matrice de la transition de l'état :

à)      

b)      

c)      

 

11) équation de la transition de l'état :

La transformation selon Laplace et quindi est eue, antitransforming a et se rappelant cela et cela au produit dans le domio de Laplace le convoluzione dans le domio correspond de l'heure ha , de lui pu² de gagner la réponse du système qui s'avère être la somme de la réponse libre et de la réponse obligatoire

 

12) l'équation de la transition de l'état commençant d'un moment les commence n'importe quel t₀ :

13) réponse au régime y_r(t) :

C'est la réponse qui est eue pour le ¥®de t qui est t₀®-le ¥ qui est .

 

14) réponse transitoire y_t(t) :

là où 2 intégrales ont été réduites à on changeant l'intégration finit opportun.

 

15) Calcolo de l'autovalori d'une matrice à :

Les solutions de l'équation caractéristique doivent être trouvées.

16) dimensions du noyau de la matrice à :

là où n il est la dimension de la matrice et du r(a) le grade qui est le nombre de lignes ou de colonnes indépendantes. Cette relation appliquée à (à lI) concourt pour estimer immédiatement la variété géométrique pour des données d'autovalore et donc pour voir moins si la matrice à laquelle il appartient peut être diagonalizzata ou.

17) Calcolo de l'autovettori d'une matrice à :

Avoir fondé ensuite l'autovalori, ils un au temps dans la matrice ( à lIest remplacé), on l'aura nécessairement qu'une ligne est décommandée et donc l'uguagliando à zéro le noyau comme l'envergure de ou plus de porteurs est caractérisé, en particulier dans le cas que la variété d'algebrica est r, alors la variété géométrique, qui est le nombre de correspondants d'autovettori, est comporté entre 1 et r, la matrice s'avère diagonalizzabile choisit si la variété géométrique est r.

18) inverse d'une matrice de T :

est eu où additionné a dans la position (ligne r, colonne c) de détermination du sottomatrice qui est obtenu éliminant la colonne r et la ligne c, tout pesé avec la matrice des signes alternés.

19) méthodes pour le calcul de la matrice de la transition du stato jle (t) = et^à :

)       une matrice de T du changement de la base constitué de l'autovettori de la matrice peut être caractérisée à cela elle le transforme en L matrice sur lequel la diagonale que l'autovalori de ce qui sont présent à elles vont il se multiplie à vous pour t et il élève à vous à et, obtenant d'une telle manière la matrice diagonale et^Lt, finalement est retourné dans la ligne du départ .

b)       la matrice doit être antitransformed selon Laplace (â")^-1 .

20) forme canonique de la Jordanie :

Les matrices qui ne peuvent pas être diagonalizzate dans combien d'autovalori de posseggono dont la variété d'algebrica est diverse de la variété géométrique, bidon cependant pour être des capacités à la forme diagonale ladite forme canonique de "a presque" de la Jordanie dans laquelle il y a des zéros d'ovunque à moins que sur la diagonale principale où il y a les blocs dont de la Jordanie chacun a immédiatement sur la diagonale l'autovalore multiple et la diagonale au-dessus de chacun des 1.

 

21) nombre de blocs d'associés de la Jordanie à vous à chaque autovalore :

Il est égal à la différence entre la dimension n de la matrice à et du grade de la matrice (à l₁I) ou, plus simplement, lui est égal à la variété géométrique de l'autovalore.

 

22) Autovettore généralisé de l'ordre k :

Ébauche d'un autovettore qu'il respecte suivre la propriété 2 :

)                   ( à l₁I)^kv_k = 0

b)                  ( à l₁I)¹0^{de k-1} v _k

 

23) procédé pour le calcul et^à par de la forme canonique de la Jordanie :

)       l'autovalori de la matrice sont trouvés à

b)       l'autovettori pour avoir l'autovalori sont variété égale estimée d'algebrica à la variété géométrique

c)       pour chacun de l'autre autovalori l'autovettori sont estimés généralisent à vous avec le procédé suivant

1)       le nombre de chaînes d'autovettori est caractérisé et donc des blocs de la Jordanie il vous associe à l'autovalore simple, un tel nombre est égal à la variété géométrique de l'autovalore au lequel peut être estimé comme différence entre les dimensions de la matrice et au grade de la matrice (à lI)

2)       la longueur d'une des chaînes associées à l'autovalore multiple est calcul estimé (à lI)ⁱ avec i = 1.2.3,… sinchè que le grade de la matrice obtenue à l'étape k 1 est égal au grade de la matrice obtenue à l'étape k, la longueur de la chaîne est donc k

3)       se rappelant les relations qui définissent le generalizzato d'autovettore ( à l₁I)^kv_k = 0 et ( à l₁I)¹0^{de k-1} v _k elle calcule le porteur_Royaume-Uni concernant le noyau de (à lI)^k et par le relazioni

v_k-1 = ( à l₁I)v_k , v_k-2 = ( à l₁I)v_k-1 … , v₁ = ( à l₁I)v₂ elles obtiennent l'altri l'autovettori de ricorsivamente concernant la chaîne

4)       si au point 2) la présence d'une autre chaîne a été trouvée, d'elle est célèbre implicitement la longueur k et donc l'autre autovettore de l'ordre k concernant le noyau de la matrice ( à l Iest trouvé)^k et de lui l'autre autovettori sont alors obtenu ricorsivamente.

d)       tout le rassemblement la trouvaille d'autovettori dans une matrice de T à vous cette porte dans la forme de la Jordanie

et)       ^{le JT} est estiméet se rappelant cela à chaque bloc de la Jordanie actuelle sur la diagonale un tel bloc : est associé

f)        on l'estime et^à = T et^JT T^-1.

 

24) comme le dépassement de l'équation d'état à la fonction de transfert :

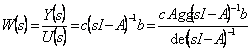Transformé de Laplace des équations d'état est e dans cette dernière limite 1° au membre 2° est zéro dans combien pour la fonction de transfert considèrent les conditions les commencent la nulle x(0) = 0, est quindi eu et le quindi regarde donc pendant que les poteaux de la fonction de transfert coïncident avec l'autovalori de la matrice de dynamique à.