Rflexion et rfraction des vagues planes
1) Incidence normale sur un matriel dilectrique :
Dans ce caso 
, pour respecter les
conditions de continuit des composantes tangentiels des champs Et et
H on engendre une vague r3flchie et une vague rifratta par
consquent les quations est 
e 
, en les projetant sur les as on obtient 
et mme 
, en substituant le
1 dans le 2 se dtermine le rapport 
dicte
coefficient de rflexion pour incidence normale, analoguement on
arrive au coefficient de rflexion pour le champ H 
, s'observe que si le champ Et est concorde, le champ H
est discorde et viceversa. Les coefficients de transmission sont 
e 
.
2) Incidence normale sur un matriel dissipativo :
Nous avons vu que pour une vague plane qui se propage dans
un demi conducteur on a 
pendant que pour la vague
qui se propage dans le moyen dilectrique elle est 
ed 
donc le coefficient
de rflexion est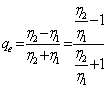 
en tant 
pour la prsence de g au denominatore qu'il tend , a que qEt @ 1 et avec des considrations
analogues
qH @le 1 donc champ Et le rifratto sera nul pendant que le champ H rifratto sera le double de cela incident mais dcade esponenzialmente en pntrant dans le moyen dissipativo pendant que dans le moyen dilectrique on instaure une vague stationnaire laquelle il n'est pas associ quelque transport de puissance.
3) Incidence oblique sur un matriel dilectrique :
Nous supposons le asse x horizontal, de l'asse y sortant
la feuille et asse z diriges vers le bas, par consquent en
supposant que la vague incident appartienne au plan xz il a que le
vecteur b a composante soit le
long de x qui de z, pour z=0 l'galit entre les composantes
tangentielles de Et porte la relation 
,
l'galit qui a pour chaque triade de champs condition que les 3
esponenziali soient gaux c'est--dire qu' 
de
cette relation drive la loi d'Erone 
et la
loi de Snell 
ainsi que en tant 
l'evidente galit entre les vitesses de phase long
x de 3 heures vagues. Pour dterminer les coefficients de
rflexion on considre deux vecteurs Et0h et Et0v locati dans le
plan orthogonal b , Et0h dirig le long y (…de
sortant de la feuille) et Et0v dans la direction 
, en se traitant
d'une vague plane a 
(…t'observes l'inversion des verseurs) en outre en
manire analogue s'crivent les champs Et et H relatifs la vague
r3flchie et la vague rifratta. En projetant Et et H de y on
obtient les relations 
e 
, en substituant le 1 dans le 2 on obtient 
laquelle en ramassant h2 et en utilisant
, 
, porte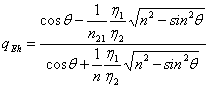 
la
, s'observe que qEh crot
monotonamente de la chaleur qui a pour incidence normale jusqu' la
valeur 1 thse pour incidence tangente.
En projetant Et et H de y on obtient les relations 
ed 
en tirant Et0v on obtient 
que,
avec des considrations analogues celles faites pour qeh il se rduit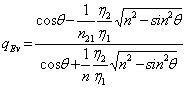 
.
De la premire expression on remarque qu'elle existe mme une
valeur q de dit angle de
Brewster pour lequel qEv s'annule, on doit avoir 
que,
labore porte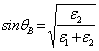 
la .
4) Incidence oblique sur un matriel dissipativo :
Les champs incidents ont la habituelle expression 
, 
comme pures les
champs r3flchis 
, 
pendant que pour les champs rifratti il faut
tenir compte qu' 
et quindi 
, 
. Pour z
= 0 on doit avoir la continuit des composantes tangentielles des
champs et donc l'galit des exposants qui est vrifie seulement
si 
qui en galant les coefficients rels
donne 
et donc dans le moyen dissipativo est parallle l'asse z
pendant qu'en galisant les coefficients imaginaires on a 
qui est encore la loi de Snell mais exposition qui 
n'est pas parallle 
et donc la vague dans le moyen pas dissipativo n'est pas plus
uniforme. De l'galit 
on peut
driver une quation relative la partie relle et une quation
relative aux parties imaginaires, de il est possible dduire et en dveloppant les
suivants cas :
a) Demi avec basse dissipation :
e
donc le vecteur de phase est le mme qui a dans le caso de moyen pas dissipativo pendant que pour je module du vecteur d'attnuation a qu'il est proportionnel la conductibilit et dpend mme de l'angle d'incidence.
B) Demi conducteur :
e
analoguement quel on avait dans le caso des vagues uniformes, je motive de cela est que la vague rifratta se propage presque orthogonalement la superficie de discontinuit quindi '/ b'qu'est vraiment la dfinition de vague uniforme.
Elle est en outre dfinie la profondeur de
pntration c'est--dire la distance de la superficie de
discontinuit laquelle le champ se rduit 
de sa valeur initiale pour de la conductibilit, a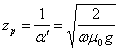 
et il s'observe comme soit infinitsimal pour un
conducteur idal (…g®), ceci est motive pour lequel
les conducteurs sont utiliss comme crans lectromagntiques et
le spessore ncessaire il diminue crotre de la frquence.
Pour dterminer les coefficients de rflexion il faut
tenir compte qui le 2 demi est dissipativo par consquent la
relation entre 
et 
avec 
du rapport
entre Et0 et H0 on dduit l'impdance de vague
superficielle 
qui seulement pour un
conducteur concide avec l'impdance intrinsque, le coefficient de
rflexion peut tre scritto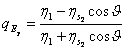 
et on
remarque que la puissance incident sur un conducteur vient presque
compltement rifratta donc la puissance de dissipe est
infinitsimale, aussi en tant dissipativo.
5) Rflexion totale :
L'angle de rfraction est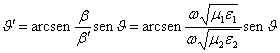 
clairement si 
(…c'est--dire si
la vitesse de propagation dans le moyen 1 est minore que dans le moyen
2) il n'a pas qu'il existe un angle limite qL tel qui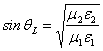 
et quindi 
c'est--dire
la vague rifratta se propage parallelment la superficie de
discontinuit.
Pour qL il a qu' 
est la plus
grande donc la vitesse de phase de la vague rifratta est moindre mais
toujours majeur de la vitesse de phase le long de x de la vague
incident comme s'est suppos 
toutefois si
la vague rifratta est pas uniforme a qu'il augmente et donc diminue la vitesse de phase de la vague
rifratta en permettant de telle manire l'galit demande des
conditions au contour, en dfinitive a que pour q < qL la vague rifratta est uniforme
pendant que pour q > qL est pas
uniforme. En ce qui concerne la puissance il a que si
nous polarisons horizontalement la vague incident, mme la vague
rifratta est polarise horizontalement et le vecteur de Poynting a
une composante imaginaire le long zde 0 donc il n'y a pas transport de puissance travers la
superficie de discontinuit mais seulement paralllement elle
puisqu'on a mme une composante relle le long de x0 du vecteur de Poynting.