La propagation guidée dans faiblement le disomogenei signifie

1)       ponceau atmosphérique :

Si l'indice de réfraction n'est pas monotone avec la quote-part mais il présente un maximum pour h = h₀ , les faisceaux qui entrent dans le ponceau avec le petit angle concernant son axe, quand ils rattrapent le correspondant de quote-part au fléchi avançé de l'indice de réfraction viennent coudé vers le fond tandis qu'ils viennent coudé vers le haut quand ils rattrapent le correspondant de quote-part au subordonné fléchi, est eus donc qui les faisceaux demeurent confinent à vous dedans autour de la quote-part h₀ .

 

2) modes guidés de la structure de la propagation une à glisser vers le bas :

Supposer d'avoir un ponceau avec l'indice de réfraction de maximum pour le h=h₀ , nous plaçons à une telle taille z=0 qui est le plan xy et supposons d'ailleurs que le propaghi d'annulation seulement le long de x. Cerchiamo une solution de l'équation des vagues du type au separabili variable , remplaçant est eu et le dividende pour T(z)X(x) les deux équations sont obtenus

.

Puisque les paramètres des moyens ne changent pas alors avec x k_X sont indépendants des coordonnées et 1ª l'équation a la solution tandis que pour 2ª l'équation que nous avons que l'indice de réfraction divers avec les coordonnées z avec le cours parabolique 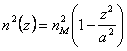donc, puisque pour l'état de separabilità est , le pu² d'équation à récrire 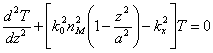dans lequel et plus tard est remplacé, l'endroit plus simple de rassemblement et devenant est atteint 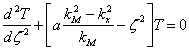le che, s'avère être l'équation de Schroedinger pour l'oscillateur harmonique d'unidimensionale, parce que lui est eue donne à théorie de quantistica cela à chaque autovalore est associé un autofunction de gauss et de Hermite (…où est le polynôme de Hermite de l'ordre m) que c'est solution de la même. Remplaçant la valeur de , la solution essayée pour l'équation des vagues est 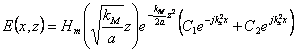où est obtenu à partir de la définition de g qui est 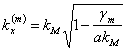est observé en particulier qui si complexe les racines sont eus qui, remplacé dans l'endroit d'élasticité de solution au vrai esponenziali qui se délabrent donc et pas à l'esponenziali complexe qui ils sont associés des oscillations périodiques.

3) vous ondule, TM e TEM :

La solution de l'équation des vagues relativement à la manière de l'ordre m est , le remplacement d'elle dans et l'application de la relation vectorial avec et et finalement de la simplification et du dividende pour jWm₀ est obtenu que la prolongation qui si et est orthogonal polarisée à la direction de propagation (VOUS) alors H possède un membre également dans la direction et le viceversa de propagation, un tel comportement peu désiré est décommandé si le trasversa dérivé du trasversa de membre change lentement. Dans l'expression de H on peut d'ailleurs définir que la rigidité de la vague qui caractérise le membre du porteur de Poynting dans la direction de propagation, en particulier pour une manière sous la coupure a une puissance imaginaire qui donc propaga.

 

4) fibre optique à la variation continue de l'indice de réfraction :

On suppose que la fibre cylindrique est caractérisée d'un indice de réfraction qui est le maximum n_M sur l'axe et diminue avec un cours parabolique jusqu'à ce qu'à la valeur minimale n_m chargiez sur le bord, la constante diélectrique a un cours parabolique qui est 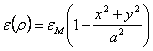. La solution de l'équation des vagues est assumée du type au separabili variable c'est-à-dire, le remplaçant a 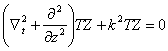, dividende pour l'ottenegono de ZT les équations, ayant comme la solution et où remplaçant donc et la valeur de et obtient 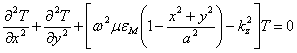où , et on peut 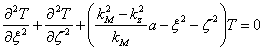placer l'ottenendo qu'ensuite pour avoir la factorisation de la nécessité une d'endroit du ce elle donne en arrière à de quel equazioni extrayant le ciascuna di.le de e qui a la forme de l'équation de Schroedinger pour l'oscillateur harmonique, à chaque autovalore correspond une solution d'autofunction de . On obtient se multiplier pour Z(z) que la solution de l'équation 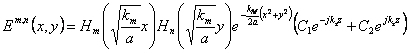de la colombe de vagues est obtenue qui est de la définition de g 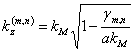qui donne l'endroit au Se de propagation .

 

5) vitesse de vitesse de phase et de groupe dans une fibre optique :

Pour la vitesse de la phase ha 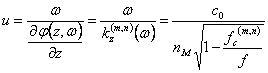, on l'observe que si le dénominateur est plus petit de 1, à la manière (n,m) dans l'issue concurrence une vitesse d'une plus grande phase de c₀ . Pour le groupe on a la vitesse 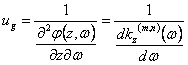à la place qui est différente de la vitesse de la phase à la confirmation que l'indice de réfraction dépend de la fréquence.

 

6) typologie de dispersion dans une fibre :

Dispersion de Modale :

L'affinchè de condition que le moyen présente la dispersion est , a dans ce cas-ci donc les moyens est dispersif en raison de la dépendance non linéaire de la constante de la propagation de la fréquence.

Dispersion du matériel :

Il est dû au fait que l'indice de réfraction de maximum qui est eu sur l'axe de la fibre, n'est pas constant mais divers avec la fréquence, un minimum de la dépendance pour m de l ₀= 1.3 est meu.

Dispersion intermodale :

Chacun dont peut être eu qui pour un indiqué fréquence de fonctionnement les sont en activité davantage qu'un mode de la propagation, est caractérisé d'un divers un u_g qu'il peut donner à endroit aux augmentations des impulsions approximativement du niveau 10ns/Km. des fibres (a=30 m m, n _M devrait être essayé pour activer une manièresimplemais aux valeursconstructives = 1.5) correspond mm de l ₀=150, pour lequel on est atténuation eue aux kilomètres beaucoup haut un.

 

7) longueurs d'onde utilisables dans une fibre optique :

L'atténuation est inférieure à 1dB/km pour des longueurs d'onde seulement comportées entre 1.2mm et 1.7mm, en fait pour de plus grandes longueurs d'onde la dispersion sont réticulaires eu tandis que pour l'absorption avançée de longueurs d'onde qui a dus la polarisation du matériel est eue.

 

8) fibres de monomodali :

L'ébauche de fibre dans laquelle l'indice de réfraction présente une discontinuité en fait il est leggermente plus grand dans le cylindre intérieur (..core) que pas dans le cap (..cladder), d'une telle manière est réussi pour obtenir une fréquence de la coupe de la manière dominante égale approximativement à 100Thz, que la longueur d'onde correspond une sujet à à faible atténuation.

 

9) fibres qui tirent profit pas des linéarités diélectriques du matériel :

Elles tirent profit du fait que la constante diélectrique dépend de l'amplitude du champ et donc elle est décrite d'une équation de Schroedinger non linéaire de laquelle on le déduit que les restes d'énergie attrapés dans une zone étroite et concourt le transport des impulsions de la courte durée sur de longues distances.