Propagation

1) contenant l'équation des vagues les améliore porteur magnétique pour des moyens de disomogeneo :

Étant le solenoidale H , parce que lui il existe des mises à niveau ils porteur à tels que , le remplacement de lui dans obtient qui a remplacés avec à dans il donne en arrière avoir tiré profit de la relation et avoir défini l'équivalent de constante diélectrique. Remplaçant l'état de Lorentz il est doit 1° le membre et définir est obtenu.

du qui le célèbre qu'également le diélectrique de disomogeneità des moyens peut être considéré comme les ouvriers électriques de sources.

 

2) contenant l'équation des vagues les améliore porteur pour faiblement des moyens de disomogeneo :

Dans la la limite peut être négligé à condition que la condition est respectée 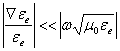donc dans le cas du VHF ou faiblement du disomogeneo le moyen est eu.

 

3) Utilizzo des mises à niveau elles porteur :

L'équation des vagues avec des mises à niveau elles porteur vient seulement utilisé quand on le trouve à nous dans la proximité des sources dedans dans la mesure où l'extérieur des sources vaut la peine la relation homogène de toute la semblable à celle-là qui puà à obtenir pour le champ électrique et pour le magnetico de champ .

 

4) équation d'eiconale et équation du transport :

L'équation des vagues pour faiblement le disomogeneo et les moyens non dispersifs est

la colombe ED , parce que elle Luneburg Kline suppose que une solution dans la forme qui a remplacé dans l'équation peut caractériser des conditions qui doivent être vérifiées, en particulier est observé qu'e(r) est le produit du mesurage pour un porteur et que le laplaciano du produit est , remplaçant et devenant plus simple est obtenu.

Développant le récapitulatif et égalant les coefficients de k₀² l'équation d'eiconale est obtenue tout en égalant les coefficients de k₀ l'équation du transport est obtenue .

 

5) vitesse de la propagation dans la direction r₀ :

L'expression de la fonction de champ électrique de l'espace et du temps qui dérive de l'expansion asymptotique de Luneburg et Kline est , celui est ébauche d'une fonction de sinusoidale a lieu du temps qui de l'espace, a cela à la croissance de t si cela considère la direction de la propagation r₀ , doit être eu duquel la vitesse de la phase dans _{le 0} est direction obtenuede r .

 

6) expression des champs et et de H en fonction de la position :

Si les petits moyens de disomogeneo sont considérés, l'expansion asymptotique de Luneburg et Kline peut être employée, dans elle si W suffisamment qu'il est élevé peut être considéré seulement des limites dominantes et₀ et H₀ e d'obtention , les remplaçant dans et tirant profit de l'ottiene vectorial de relation 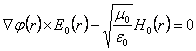tout en remplaçant dans elle est obtenue . Le remplacement dans l'entrambe , dérivant de l'équation d'eiconale, et la rigidité intrinsèque de la moyenne est obtenu :

là où s₀ sont le débiteur dans la direction de cela est est orthogonal à superficiel l'equiphase ceux.

 

7) rigidité intrinsèque locale :

 

8) faisceaux électromagnétiques :

L'ébauche des courbes qui dans chaque point sont orthogonales sur la surface de propagation, le long d'eux propaga l'énergie électromagnétique, car il peut observer du porteur de Poynting où la relation vectorial ₀ a été employée et étants le débiteur orthogonal à superficiel de la vague j(r) = costante. les caractéristiques de la trajectoire des faisceaux peut être desunte de l'équation d'eiconale par laquelle est gagné, la relation dont est déduite que les restes de faisceau confinés dans le plan caractérisé de s ₀ et et ont courber c'est lui a la concavité tournée vers la région avec l'augmentation de l'indice de réfraction, comme exemple pour l'atmosphère l'incurva de faisceau vers le fond dans combien le plus est approché à nous la terre, plus qu'il augmente à la concentration et donc à l'indice de réfraction.

 

9) loi de Snell généralisé :

À partir de l'eiconale l'équation est obtenue appliquant le rotor et se rappeler la putréfaction grad[. ] = 0 de che a dont le théorème charge l'obtention peut être appliqué, choisissant donc un circuit rectangulaire en lequel au côté avançé un indice de réfraction n et au côté inférieur correspond un indice de réfraction n vers le bas, faisant pour s'étirer à zéro que les côtés verticaux est obtenus où q il est l'angle inclus entre s₀ et descendant vertical z₀ .

 

10) principe de Fermat :

Il affirme que la longueur de la distance électromagnétique est stationnaire qu'est le propaga électromagnétique d'énergie le long de la trajectoire qui rendent le minimum la valeur de L.

 

11) cours des faisceaux dans des moyens stratifiés radialement :

Dans des moyens stratifiés radialement, l'indice de réfraction a la symétrie radiale, il obtient que les restes de faisceau confinés dans un plan passant pour l'origine de la structure sphérique et contenant s₀ .

 

12) cours des faisceaux dans les moyens stratifiés lentement :

Les moyens stratifiés sont lentement des moyens pour lesquels on déduit l'indice de réfraction divers seulement avec la quote-part z, du qui le faisceau demeure toujours confiné dans un plan orthogonal au plan xy, obtient que si q est l'angle inclus entre s₀ et z₀ , est eu.

 

13) faisceaux dans le troposphere :

Ébauche de la partie inférieure de l'atmosphère qui va de 0 à 10km aux poteaux et de 0 à 15Km à l'équateur, il est constitué à partir de l'azote (78.1%), de l'oxygène (20.9%), de la vapeur de l'eau jusque 2'à un maximum de 5% et d'autres gaz. L'indice de réfraction divers avec la quote-part en fonction de la densité et le polarizzabilità des membres simples, au niveau de la mer vaut la peine 1.0003, afin d'estimer des petites variations qu'il vient a défini la réfringence que pour l'atmosphère au £ 40GHz de f vaut la peine d'être p_t le total de pression atmosphérique et p_W la pression partielle de la vapeur de l'eau et donc la première limite est la limite sèche ayant des valeurs élève à vous mais l'écurie dans combien a comporté entre 265N et 284N tandis que la limite célèbre supporte des variations fortes pouvant passer de 102N 31N. On l'observe que la réfringence diminue en second lieu à la croissance de la quote-part h où N_s est la valeur de la réfringence _{aux 0} terres eth la taille caractéristique qui vaut la peine approximativement 8Km, ces valeurs changent en particulier dans les conditions météorologiques donc à une basse altitude sont eus :

)       l'atmosphère inférieure si unité de N/Km

b)       norme de l'atmosphère si unité de N/Km

c)       superstandard de l'atmosphère si unité de N/Km.

 

14) équivalent de faisceau de terre :

Dans le cas des raccordements entre les stations situées à la terre est eu d'ailleurs que l'angleq entre la tangentedu débiteur s ₀ avec le faisceau électromagnétique et dirigent radialement vers le fond est approximativement 90° donc que courber est, considérant que courber de la terre est peut être fait à un changement de coordonnent qui décommande courber du faisceau électromagnétique simplement au pacte pour magnifier la terre. D'ailleurs être ha , un regarde cela si puis R_et®¥ et donc le propaga d'énergie parallèlement à la surface de terre, qui est établit un ponceau électromagnétique.

 

15) visibilité entre les antennes :

Deux antennes indiquent pour être dans la visibilité quand le faisceau électromagnétique qui combine à elles n'intersecte pas la surface de terre, puisque le faisceau électromagnétique présente la concavité tournée vers la terre est eue qui la visibilité électromagnétique est plus grande de la visibilité géométrique.

 

16) Approximation WKB :

Remplacement dans l'équation du transport qui est gagné de l'eiconale il obtient en quel :

)       vu un débiteur t₀ orthogonal à s₀ peut être décomposé le gradient dans ces deux directions et donc écrire

b)      

c)       pour la définition de divergence, vu qu'avoir la section de streamtube les commence S, est eu .

Le remplacement est obtenu pour laquelle s'est multiplié et₀^* et simplifié donne de retour 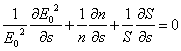cela est des limites qui jaillissent du dérivé d'un logarithme, après que tout ait 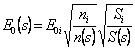tandis que pour la limite de la phase de l'expansion de Luneburg et de Kline est eu, l'approximation WKB déterminent la valeur du champ à l'abscisse curviligne s .

 

17) cours du champ dans faiblement des moyens dispersifs de disomogeneo :

L'équation d'eiconale étant avec (…le compte de prises donc est des dissipations dus à la conductivité qui de ceux dus à la polarisation), n'est pas satisfaite moins que la fonction que la mettent en phase n'est pas une fonction complexe , remplaçant une telle expression dans l'eiconale et égaler les vraies pièces est obtenu tandis qu'égaler les pièces imaginaires est eu où superficiel est orthogonal à l'equiampiezza, l'expression du champ devient .

 

18) cours du champ dans faiblement le disomogeneo et faiblement les moyens dispersifs :

Les moyens sont faiblement dispersifs si 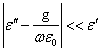aussi on obtient le complexe restant qui est si l'indice de réfraction, est eu que la vraie partie règne clairement sur la partie imaginaire, que l'equiphase et superficiel superficiels l'equiampiezza coïncide, e 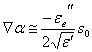, remplaçant de telles expressions dans l'équation du transport 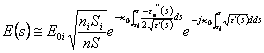est trouvé et donc un vrai exponentiel est eu également qui atténue le champ à la croissance de s. En particulier il vient a défini l'atténuation spécifique des moyens à l'abscisse s et 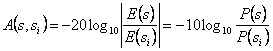l'atténuation supportée du champ dans la distance entre s et s.

 

19) vague non homogène :

Ébauche d'une vague pour laquelle la superficielle de la vague est dans chaque point orthogonal à le superficiel d'amplitude.