Irradiation électromagnétique
1) la fonction à l'élever du vert :
Dans l'électromagnétisme une réponse impulsive dans
l'espace dans la façon dont beaucoup est considéré les sources a un
cours de sinusoidale du temps mais eux sont ovunque nul à moins que
dans le point r 'dans ce qui sont ils placiez, il concourt pour
déterminer les largenesses électromagnétiques produits de la source
dans les points r de l'espace, notamment la réponse impulsive peut
être des mises à niveau déterminées qu' 
ils le
porteur dans ce cas coïncide avec la fonction à l'élever du vert,
ou le pu² pour déterminer le champ 
où le stavolta
la réponse impulsive est la fonction de diadica du vert qui est plus
complexe s'occupant qu'un porteur. Afin de déterminer la
fonction à l'élever de la référence verte est faite à l'équation
des vagues à s'élever (…projeté sur un des as
cartésiens) en présence d'impresse impulsif de courants de l'espace 
dont la fonction à l'élever du vert est solution.
L'origine du système des coordonnées est le point où la
source est placée, si nous considérons l'équation précédente dans
les points externes à la sphère qui comporte des sources a 
de quel dividende pour r et prendre le rG de solution
est eu dont la solution est la somme d'une vague
progressive et d'une vague régressive, ne vient pas considéré dans
combien physiquement n'a pas le sens une vague qui collassa. Le
dividende pour r trouve l'expression de la fonction à l'élever du
vert 
où le coefficient C s'avère intégrer
l'équation 
sur le volume sphérique de contenir le
faisceaur les sources 0, en utilisant les coordonnées sphériques et le
dividende pour r2 
est obtenu qui,
effectuant la porte de calculs 
à cela pour r®0 devient infini mais vu les infinites de l'ordre avançé
et de devenir plus simple 
est obtenu et donc 
. Après que tout le lequel de l'espace les améliore
porteur d'un point soit trouvé avec de la La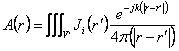 
prolongée au seul volume qui contient des sources.
En particulier dans le cas d'une source impulsive 
est trouvé dont le rotor dans des coordonnées
sphériques, deviennent un compte plus simple de possession qui 
pour par l'intermédiaire de de la symétrie axiale de la
source, donne
et est donc toujours orthogonal à la source, le
remplacement d'elle dans 
obtient 
donc des mensonges dans un méridien qui contient la
direction des sources. À partir les précédents la fabrication 
le du champ d'induction est obtenue tandis que la
colonne 
obtient le champ d'annulation.
2) irradiation des sources des dimensions finies :
Une source plus impulsive est considérée mais que des
dimensions finies, un son point est pris comme l'origine du système
des coordonnées, tous les autres points de la source pour être r
éloigné 'de lui et R du point p d'observation ce à la place TOS
soit r éloigné de l'origine. Le champ de H est gagné des
mises à niveau elles le porteur auquel la fonction est legs aux
sources par la réponse impulsive…(à l'élever du vert) 
, clairement pour r®0 des
limites dans la parenthèse considère seul 
tandis
que pour le ¥®de r on le
considère j solob .
L'intégrale qui obtient pour le champ à la grande distance 
devient plus simple dans combien si la dimension du
maximum D de la source est beaucoup de mineur de la distance de R
(…entre un point de la source et le point p) est eu qui le
débiteur R0 @ r0 et est donc
constant en volume de V'qui enferme la source et peut être porté
dehors de l'intégral, comme pur au dénominateur @ r de R tandis que dans l'argument de
l'exponentiel 
est remplacé où 
est le débiteur dans la direction que cela se joint
l'origine avec le point p de source 'ce ce TOS soit r éloigné
', après que tout l'ha 
se remplaçant dans soit obtenu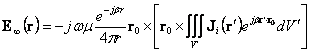 
.
Le carateristiche des champs obtenus sont décrits de l'état d'annulation :
.
3) réciprocité électromagnétique :
Le champ produit à partir d'une source monochromatique à 1 constitué à
partir de l'impresse magnétique J m1de
courants et des ouvriers électriques i1de J satisfait les
équations 
, tandis que pour la
source 2 analogue à l'opération à la même fréquence a 
, se multiplier respectif pour H2 , et2 , - H1 , - et1 et ajouter le membre au membre obtient
à 1° le membre une quantité qui avec le solità identité
vectorial elle vient apporté de nouveau à 
.
Intégrant au 1° et au 2° le membre sur un volume V qui contient
les sources, à 1° le bidon de membre après que tous soient
appliqués au théorème de la divergence obtenant le théorème de la
réciprocité valide pour l'isotropo de moyens 
et
soient tracés où le compte a été gardé qui les sources i1et J m1de
J n'est pas nulle choisissent en volume V1 que la source à 1 contient et analogue pour la
sourceà 2. Des conditions
d'annulation on déduit que le champ à l'infini devient donc
intégration infinitésimale sur un volume V qui contient toutes les
annulations de l'espace le traverser la surface de S qui l'enferme et
l'égalité des réactions est eue 
donc de quel
suivre peut être alerte déduite à vous :
) vu absent l'impresse magnétique de courants dans deux dipöles minces qui peuvent être contenus deux cylindres et en décomposant l'intégrale du volume de la série d'une intégrale de la surface que pour la présence de J le courant caractérise et d'une intégrale de ligne, pour dont la présence et, caractérise la tension V, le dividende pour I1I2 obtient l'égalité des stiffnesses mutuels.
b) On a eu l'application de
l'égalité des réactions à une source à et à une source impulsive
d'espace d'essai 
ayant qui concourt pour gagner le
champ produit à partir de la source à dans un point r.
4) théorème de l'équivalence :
On le suppose d'avoir une source à et une source d'essai
unitaire qui concourt pour estimer 
la réaction,
parce que l'égalité des réactions elle est également égaleau tA , le théorème de la
réciprocité sur un volume est considéré mais qui contient tout le
volume de l'espace ad.eccezione.del au lequel contient la source à et
est inclus de la surface de S , d'une
telle manière n'a pas l'intégrale sur le volume joint de Sà , obtient 
à partir
de ce qui par la colombe vectorial 
de relation 
est ouvrier électrique obtenu est superficiel le
courant tandis qu' 
est magnétique le courant
superficiel.
Il a lui-même donc que le champ et le nella 0 directionsde produit de t lui donne que la source à est le même produit les donne aux équivalents superficiels de courants qui trouvent sur une surface qu'elle enferme la source à.
