Dispersion

1) vitesse de phase et de groupe d'un champ presque monochromatique :

Vu la limite dominante simple actuelle et₀(s) dans le développement de Luneburg-Kline et à supposer qu'il est vrai, est eu que l'expression du champ en fonction du temps et du s est le j est dans ce cas-ci ignota donc est approchée de 1° l'ordre au moyen de tailleur et le remplacement également 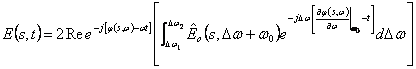est eu où le 1° exponentiel est relativement à une taille périodique avec la pulsation W₀ qui propaga avec la vitesse 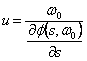de la phasetandis que le 2° exponentiel il module dans l'espace et le temps le 1° exponentiel, et l'enveloppe est dit, à elle correspond une vitesse de groupe .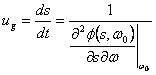

2) l'état de l'égalité entre le groupe et la phase expédient :

_ la vitesse d'uguagliando de la phase et le group velocity di gruppo et portent le dénominateur au numérateur du membre vis-à-vis de, obtiennent qui soit vérifie le Se , remplace dans lui et simplifient l'ottiene et le quindi qui soit seul vérifient si l'indice de réfraction di rifrazione pour ne pas dépendre de W.

 

3) propagation d'un champ non monochromatique :

Porter à la fréquence W ₀ a modulé en ayant l'amplitude d'une impulsion gaussienne est considéré durée les commence donc l'expression del field , l'inscription le cosinus dans des gains exponentiels de forme transformés du nel de Fourier du point les commence 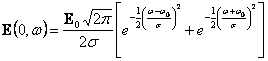cpstituita de deux bandes gaussiennes d'amplitude 4- W dessus centrépar s₀ et W₀ . La valeur de transformée de Fourier dans le point s est se multiplier gagné pour , l'antitrasformandola l'obtient 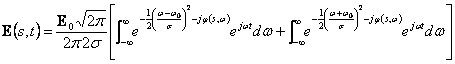contient la fonction d'eiconale qui est incognito, toutefois pour que le pu² 1° intégral soit remplacé avec un développement en série a arrêté à 2° l'ordre obtenant en ce que qui effectue la substitution et plus tard e il est obtenu, toujours pour le 1° analogue qu' intégral il est procédé pour l'intégrale 2° où le stavolta pour la concordance avec les positions précédentes pour la fonction d'eiconale le développement est eu d'où moins de présent sur le dérivé avant lui détermine la définition les largenesses ont conjugué concernant les précédents et obtiennent donc, pour l'intégrale 2° . Remplaçant les deux qu'elle s'avère à vous trouve à vous et se rappeler cela a .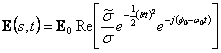

 

4) facteur d'amplitude :

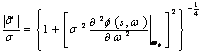
donc avec l'augmentation de de la distance couverte l'amplitude du champ diminue.

 

5) facteur de transport :

à elle la forme de l'impulsion est attachée qui est encore gaussienne mais elle change son amplitude qui est plus grande après la propagation. Le facteur du transport dans combien dans lui s'appelle est présent est le temps qu'on peut gagner l'espace et donc la vitesse de l'impulsion gaussienne qui est trouvée est égale à la vitesse de groupe.

 

6) durée de l'impulsion :

donc avec l'augmentation de de la distance couverte augmente la durée de l'impulsion.

 

7) différence entre les moyens dispersifs et les moyens dispersifs :

On l'a que les moyens dispersifs transforment l'énergie électromagnétique dans la chaleur pour l'effet de Joule alors que les moyens dispersifs ne transforment pas l'énergie électromagnétique dans une autre forme d'énergie mais simplement elle la redistribue dans l'espace, donc si nous l'envoyons à une impulsion dans des moyens dispersifs qu'elle augmente et elle diminue l'amplitude du champ.