Aléatoire variable
1) aléatoire variable :
Ébauche d'une fonction qu'elle a pendant que le dominion l'intégralité de S de s'avère vous d'une expérience et comme le codominio avec des vrais nombres.
2) fonction de distribution cumulative :
Elle laisse mesurer la probabilité qu'aléatoires variables le X assument que de plus petites ou égales valeurs à des données évaluez x
3) propriété de la fonction de distribution :
) FX(-¥) = 0 FX( ¥) = 1
b) FX est une fonction non décroissante monotone, celle est si le £X 2 de x1 > FX(£de x 1) FX(x2)
c) P{X>x} = 1 - FX(x)
d) la fonction de distribution
est continue du destra ![]()
et) P{x1 < £ X de X2 } = FX(x2) - FX(x1)
f) le saut de la fonction de la distribution dans la correspondance d'un point de discontinuité X0 est égal à la probabilité que la variable assume la valeur X0
4) aléatoire variable du type continu :
Une parole aléatoire variable de x de type continu si sa fonction de distribution est continue.
5) aléatoire variable du type discret :
Une parole aléatoire variable de x de type discret si sa fonction de distribution est une fonction aux étapes.
6) aléatoire variable du type mélangé :
Une parole aléatoire variable de x de type mélangé si sa fonction de distribution est ligne de traitement en différé mais pas aux étapes.
7) empiricist de distribution :
Un empiricist de distribution est une fonction aux étapes ayant comme des points du dominion les valeurs de la variable le correspondant aléatoire aux résultats de l'essai, à chacun d'elles que l'empiricist de fonction associe une étape 1/n de taille.
8) percentile :
Le percentile u (ou le n-esimo de percentile) d'aléatoire variable le X est qu'une telle valeurX u ce £ X ude P{X} = u. Le percentile de fonction est donc l'inverse de la fonction de distribution. Dans autre le percentile de 10 mots indique que la valeur de x pour laquelle le secteur dont va -subtended le ¥ à x et de la fonction de distribution est égale à 10%.
9) médiane d'aléatoire variable le X :
L'ébauche du percentile de la valeur 0.5 et a été indiquée avec le m. de lettre.
10) densité de probabilité de fonction :
La densité de la probabilité fX(x) est définie comme le dérivé de la fonction de
distribution ![]() .
.
11) propriété de la densité de probabilité :
) la fonction de densité (x) n'est pas le ³négatif0 de f X
b) FX(x2) - FX(x1)
= ![]()
c) FX(x) = ![]()
d) ![]()
et) P{x1 < £ X 2de X } = ![]()
12) fonction de la masse des probabilités variables pour aléatoire :
Ébauche de la fonction pk = P {X = xk}.
13) valeur prévue :
La variable la valeur prévue d'un aleatoria X est le centre de la gravité de la densité ou les masses de la probabilité dans les caisses continues ou respectif discret. En d'autres termes c'est la valeur moyenne de la distribution.
14) la valeur prévue variable de aléatoire continue :
![]()
15) valeur prévue d'un discret aléatoire variable :
![]()
16) propriété des statistiques moyennes :
) E[a*X ] = a*E[X ]
b) E[a*X b*Y ] = a*E[X ] b*E[Y ]
17) désaccord :
Le désaccord variable aléatoire d'un X exprime une mesure du âconcentrazioneâ? des valeurs assumées d'un aléatoire variable autour de sa valeur moyenne.
![]()
18) ligne de manoeuvre norme :
C'est la racine du désaccord
![]()
19) le désaccord variable de aléatoire continue :
![]()
20) désaccord d'un discret aléatoire variable :
![]()
21) relation quadratique entre la moyenne et le désaccord :
![]()
22) moment de l'ordre n d'un X aléatoire variable :
mn = E[Xn]
23) le moment les centre de l'ordre n d'un X aléatoire variable :
![]()
24) inégalité de Chebyschev :
![]()
25) inégalité de Markov :
![]()
26) de variable indépendant statistiquement :
Deux X et Y aléatoires variables indique statistiquement
le indépendant si, donné 2 ensembles arbitraires et à B des valeurs
de X et de Y respectifs, il est eu ![]() .
.
27) uniforme aléatoire variable :
La variable que aléatoire continue X indique l'uniforme
entre ![]() e
e ![]() si sa densité est
constante dans l'intervalle
si sa densité est
constante dans l'intervalle ![]() nul et ailleurs.
nul et ailleurs.
28) gaussien aléatoire variable :
La variable que aléatoire continue X est ledit gaussienne si sa fonction de densité est de la forme
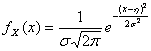
29) norme gaussienne variable :
Ébauche nulle d'un gaussien variable avec le milieu de valor et le désaccord unitaire.
30) fonction de densité d'un exponentiel aléatoire variable :
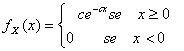
31) fonction de densité d'un iperexponential variable :
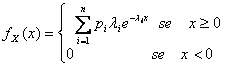
32) fonction de densité d'un Rayleigh distribué aléatoire variable en second lieu :
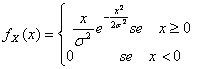
33) fonction de densité d'un lognormale variable :
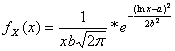
34) fonction de densité d'une variable distribuée selon le modèle de gamme :
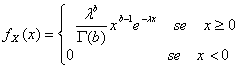
35) fonction de densité d'un aléatoire variable distribué selon l'qui-image modèle :
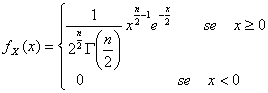
36) fonction de densité d'un aléatoire variable distribué selon le modèle d'Erlang :

37) fonction de densité d'un étudiant distribué aléatoire variable en second lieu :
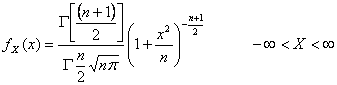
38) fonction de densité d'un aléatoire variable distribué selon le modèle de K :
![]()
39) fonction de densité d'un aléatoire variable distribué selon le bêta modèle :

40) fonction de densité d'un aléatoire variable distribué selon le modèle de Cauchy :
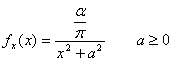
41) fonction de densité d'un aléatoire variable distribué selon le modèle binomial :
![]()
42) fonction de densité d'un aléatoire variable distribué selon le modèle géométrique :
![]()
43) Poissoniana aléatoire variable :
Si l il est un paramètre et entier aléatoire de X un et positif variables.
![]()
44) loi des grands nombres :
Dans une série de n répété examine, dans lequel la
probabilité de la réussite d'un essai simple est égale à p, le
rapport entre le nombre de succès k et le nombre de bouts droits des
essais n avec p quand ¥ ® de n , ![]()
45) le théorème les centre de la limite pour des fonctions binomiales :
Dans une série de n répété examine, indiquant avec X le nombre de succès, variable de constructions le Y aléatoire
![]()
La distribution de la probabilité FY(y) est telle que 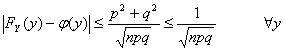
46) fonction de distribution d'une fonction variable d'aléatoire :
La fonction de la distribution FY(y) assure le £ y de la probabilité P{Y}
47) théorème fondamental de la densité de probabilité :
Pour une valeur spécifique y de la densité fY(y) est donné le da 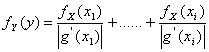
48) valeur prévue d'un aléatoire variable Y = g(X) :
![]()
