Statistiques mathématiques
1) estime pour des intervalles :
Ébauche d'avoir l'estime l'objectif à caractériser entre toutes les valeurs I de c1 et de c2 pour lesquelles {c1 < X < 2C } = g, celui-là de la longueur minimale.
2) vérification des statistiques d'hypothèses :
La branche de la théorie de la décision basée sur le choix entre 2 fonctions des distributions de la probabilité est une.
Laditehypothèse basse de H 0
Laditealternative d'hypothèse de H 1
3) Spazio des événements :
Il est avec des événements possibles entre lesquels choisir, est indiqué avec M.
4) Spazio des marques elles :
Il est avec de toutes les formes possibles de vague sended à l'observateur, est indiqué avec S.
5) Spazio des observations :
Il est avec de des tous les possibles les marque des reçus, est indiqué avec Z.
6) Spazio des décisions :
Il est avec de des tous les possibles s'avère vous du procédé de décision, est indiqué avec D.
7) règle de décision :
Ébauche d'une règle de determinist qui s'associe à chaque décision de l'observation une.
8) l'erreur de 1° saisissent une décision binaire après observation simple :
Une erreur du type 1° est eue si l'hypothèse H0 vient également rejeté étant vraie.
9) l'erreur de 2° saisissent une décision binaire après observation simple :
Une erreur du type 2° est eue si l'hypothèse correcte est H1 mais elle s'avère vous de l'expérience ne soutiennent pas le refus de H0.
10) Critère du verosimiglianza maximum :
La règle de décision choisit l'événement qui a une plus grande probabilité pour avoir causé l'observation.
11) rapport de verosimiglianza :
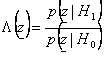
12) Critère de Neyman - personne :
Il caractérise une règle de la décision qui diminue b , ayant fixé à .
13) différence entre l'estime de paramètre et la vérification des hypothèses :
L'estime de paramètre concourt par les observations sur un modèle simple à l'évaluation de ou à plus de paramètres tandis que la vérification des hypothèses met aux modèles de la comparaison 2, à celui-là de l'hypothèse nulle et à celui-là de l'alternative d'hypothèse.
Nombres accidentels
14) définition fonctionnante de nombre accidentel :
L'ordre des nombres accidentels est on s'avérant d'une expérience physique
15) définition conceptuelle de nombre accidentel :
L'ordre d'aléatoire variable est un i.i.d.
16) modalité pour la génération des nombres accidentels :
à) par des tables
b) par des algorithmes de congruenziali
17) décrivent un générateur de ricorsivo accidentel de nombres :
La partie d'une valeur les commence et silicium elle obtient la valeur successive en fonction de la valeur précédente.
18) décrivent un générateur de congruenziale accidentel de nombres :
La valeur actuelle est basée sur le concept de congruenza donc qu'ils est legs au reste de la division pour m de la valeur précédente.
19) méthode afin de produire des nombres accidentels avec un donné la distribution par un calcul :
(u) est nécessaire pour calculer les valeurs de la fonction-1de F pour u = ui , étant {u} un ordre des nombres accidentels uniformes.
20) décrivent le bâti Karl de méthode :
Il est basé sur un prélèvement accidentel et employé comme exemple pour le calcul des intégrales, dans N pratique est porté dehors chronomètre une expérience aléatoire et alors on l'estime la moyenne de tous les tours dehors obtenus à vous.
Théorie de l'estime
21) estime de point :
Ébauche d'une fonction de l'observation X il è 
= g(x)
22) priseur :
L'ébauche d'une fonction de porteur X a constitué à partir de toutes les
observations X il è = g(X)
23) erreur de l'estime :
C'est la différence entre le priseur et incognito le
cioè du paramètre
q et = - q
24) polarisation du priseur :
Ébauche du milieu de valor de l'erreur du b(de
stima) = E(- q)
25) désaccord d'un priseur :
C'est la valeur prévue de la place de l'erreur de
l'estime V() = E[ (- E())2 ]
26) priseur de consister :
Un priseur consiste si l'erreur d'estime s'étend à 0 pour N qui s'étend à infini.
27) priseur optimal :
Il est le priseur qui diminue le milieu quadratique
d'erreur e = E[ (- q)2 ]
28) décrivent l'estime pour des intervalles :
Ils viennent ont défini un croisillon des fonctions de
l'observation1 = g 1 (x) e 2 = g 2 (x) qui
définissent un intervallo à l'intérieur duquel le paramètre q est contenu avec une
probabilité g.
29) objectif de l'estime pour des intervalles :
Pour diminuer la longueur de l'intervalle |1 - 2 | .