Questions de la théorie des phénomènes aléatoires

1) les définitions statistiques de la probabilité et de leurs cravates :

Il y a 4 définitions possibles pour la probabilité :

) à axiomatique

La probabilité de l'événement sûr est unitaire.

La probabilité est un nombre comporté entre 0 et 1.

La probabilité d'un événement qui est somme de deux n'ayant pas des éléments d'événements en commun est la somme des probabilités.

b) Fréquence de répétition

La fréquence relative d'un événement à est le rapport entre le nombre d'essais dans des lesquels un élément a lui-même comme le résultat avec à et le nombre d'essais, quand s'étendent au ¥ , la fréquence relative s'étire à la probabilité.

c) Classique

La probabilité d'un événement à est le rapport entre le nombre de le possible s'avère à vous favorable à l'événement à et le total de nombre de le possible s'avère à vous. Une amélioration de la définition exige que la simple s'avère à vous est equiprobabili.

d) Subjective, la probabilité est le prix qu'un individu pense loyalement pour payer afin de recevoir 1 si la vérification d'événement.

2) le paradoxe de Bertrand :

C'est un legs de paradoxe à la définition classique de la probabilité et cela il le met dans la crise quand le nombre de le possible s'avère à vous qu'il est sans limites. Une circonférence C de faisceau est r eu, doit être estimée la probabilité qu'une corde choisie ab au cas a de plus grandes dimensions du côté de la triangle équilaterale enregistrée dans la circonférence, trouvera donc au moins trois divers ceux s'avère à vous tout les justes :

) ils considèrent le soleil ayant des cordes le centre à l'intérieur du cercle de faisceau , la probabilité dans des classiques de limites peuvent alors être exprimés comme le rapport entre 2 secteurs, le secteur du cercle en lequel il peut tomber le centre de la corde et le secteur de C, la probabilité exigée vaut la peine le ¼.

b) a fixé une extrémité de la corde, constatera que l'autre extrémité doit être comportée dans un angle égal avec 1/3 du périmètre de la circonférence, donc la probabilité est dans ce cas-ci 1/3.

c) les cordes plus longues sont horizontales imaginé et avec l'ancien tra comporté et , constatez dans ce cas-ci que la probabilité vaut la peine le ½.

3) théorèmes du total et du Bayes de probabilité :

Le théorème du total de probabilité affirme cela si une cloison de l'espace témoin est S eu dans des événements de m_{à 1}...,_{À m} et à un événement de B définis sur S alors la probabilité de B est donnée de la relation, est démontrée écrivant B comme intersection avec l'espace témoin et donc avec la cloison_{à 1}...,_{À m} , décomposant et puis employant la probabilité conditionnée.

Le théorème de Bayes concourt pour des moyens du théorème du total de probabilité a posteriori de gagner la probabilité d'un événement concernant une cloison₁...,_{À m} de S sachant sa probabilité a priori, c'est lui est eu . On gagne de l'égalité qui jaillit de la probabilité conditionnée et d'employer le dénominateur le théorème du total de probabilité.

4) statistiques de l'indépendance des événements variables et aléatoire :

Deux événements sont statistiquement indépendant si la probabilité de l'intersection d'événement est égale au produit des probabilités des événements simples . Deux ceux aléatoires variables sont à la place statistiquement indépendant si donné deux avec arbitraire à et est-ce que B des valeurs de X et de Y respectifs, P{X est eu ? À, Y ? B} = P{X ? } à P{Y ? B}.

5) la probabilité conditionnée : Définition et interprétation en termes de fréquence relative et sa propriété :

C'est la probabilité qui a lieu un événement ensuite à cet événement B a été eue lieu . En termes de fréquence relative, la probabilité conditionnée de à des données de B est approximativement égale à la fréquence relative avec laquelle on présente l'événement à dans la succession des essais dans lesquels l'événement de B est présenté.

6) essais répétés et loi binomiale :

Ébauche des essais qui produisent d'un espace égal témoin au produit cartésien des espaces S étant n le nombre d'essais et S témoin de n l'espace témoin des résultats de l'essai simple. Les essais de Bernoulliane sont à la place une caisse particulière des essais répétés, dans combien les essais coûtent entre de indépendant eux et 2 sont seule alerte possible à vous. Elle est parlée au lieu des essais généralisés de Bernoulliane si chaque essai a r possible s'avère à vous.

La distribution des succès est décrite de la loi binomiale, en particulier le nombre des succès dans n'importe quel ordre est tandis que le nombre de succès dans n'importe quel ordre est .

7) la fonction de distribution est définie et si d'elle ils montrent la propriété :

La fonction de distribution est susceptible de décrire la probabilité qu'un événement est eu lieu est comporté dans un intervalle de données, il est décrit de la terminologie donc que la fonction de la distribution d'une valeur variable sûre X d'aléatoire le X caractérise la probabilité que X ont la valeur inférieure à x. Ayez la propriété suivante :

) elle est comportée entre 0 et 1 devant représenter une probabilité.

b) elle possède des discontinuités de saut qui sont des solos continus de droite et dont la valeur est égale à la probabilité qu'aléatoires variables le X assument la valeur X dans l'issue .

d) Si x₁ < x₂ puis

et) la fonction croissante est une monotone.

8) ils sont écrits et la propriété de la densité de probabilité sont démontrées :

La densité de probabilité est définie comme le dérivé variable concernant aléatoire le X de la fonction de la distribution , donc l'intégrant entre 2 points X₁ et x₂ la probabilité est obtenu que le X sont comporté dans cet intervalle ; de celui il suit que l'intégrale prolongée à tout le vrai axe doit être en valeur 1.

9) la densité de l'empiricist de probabilité (histogramme) et de son interprétation en termes de fréquence relative :

L'axe X dans les intervalles de l'amplitude de D est subdivisé , après quoi une expérience est exécutée des temps de n et une étape de taille est associée à chaque proporziona d'intervalle de D qu'ils au nombre de s'avère à vous qu'ils tombent dans l'intervalle, obtient donc un histogramme qu'il doit être normalisé de sorte que le secteur de subtended le soit unitaire ; elle s'étend à la fonction de la distribution pour

¥ ®et D 0®de n.

10) les inégalités de Chebyschev et de Markov : démonstrations et applications possibles :

Tous les deux résolvent pour faire pour limiter pour déterminer des inégalités qu'elles donnent une idée dessus de même qu'est distribuée la densité de probabilité.

L'inégalité de Chebyschev affirme que la probabilité qu'aléatoires variables le X supposent que des valeurs externes à un intervalle arbitraire (net , n et) est négligeable si le rapport s/et est suffisamment petit :. Elle est obtenue installant la solution comme le désaccord des deux masses de probabilité.

L'inégalité de Markov affirme à la place que la probabilité cela .

11) variable l'exponentiel aléatoire et ses moments de l'ordre 1 et 2 :

Sa densité de la probabilité est indiquée de . Le moment de l'ordre 1 le moment de l'ordre 2 est obtenu à partir du moment de

12) c aléatoire variable² :

Une propriété importante est que la somme des places des normes indépendantes gaussiennes de n est un C² avec des degrés de liberté de n. Beaucoup dans les statistiques pour le calcul du désaccord des fonctions gaussiennes au milieu de valor est incognito une distribution utilisée, qu'on le trouve lui sont distribués comme un C² avec des degrés de la liberté n-1 où n dans pratique il coïncide avec la dimension de l'échantillon.

13) aléatoire variable le géométrique :

Sa densité de somiglia binomial de probabilité beaucoup à un moins qu'exponentiel . Sa valeur prévue est qui est obtenue pour la comparaison avec le dérivé de la série exponentielle.

14) la loi des grands nombres :

Elle affirme que la probabilité que la fréquence relative diffère davantage de la probabilité en ordre qu' et vallée 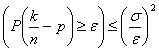. On le démontre appliquant simplement l'inégalité de Chebyschev et se rappelant que le nombre de succès est distribué un binomial avec le npq de désaccord deuxièmes.

15) le théorème de la limite les centre ; pour donner ou plus déclare à vous et pour indiquer une ou plusieurs applications :

) quand le ¥ de npq®de produit que le binomial s'étire à le gaussien.

b) le convoluzione de n gaussien est toujours un gaussien

c) la distribution variable de la somme de bouts droits aléatoires de n, à la croissance de n, un gaussien. Si le variable est continu également la densité gaussienne de densité rapproche un.

d) Si X₁ ..., X_n est i.i.d. aléatoires variables avec le milieu h de valor et le désaccord s² puis pour le ¥®de n que la variable s'étire à une norme gaussienne.

16) l'approximation de Poissoniana de Binomiale(Teorema di Poisson) déclaré et démonstration :

Dans le cas des événements rares qui est des essais répétés pour des lesquels la probabilité de réussite est plus petite de 10%, elle est s'assemblent pour rapprocher binomial avec le Poissoniana dont la densité de la probabilité est décrite du, en lequel le l c'est la valeur prévue et il vaut la peine le np étant n le nombre d'essais et probabilité de réussite de p de. Le théorème est démontré au congé de la formule de Bernoulli tirant profit que n > > k et n > > np donc pour q = 1-p = et^{- p} il a pu employer le développement du tailleur valide dans le cas de p infinitésimal. Le remplacement est trouvé.

17) le théorème fondamental : densité de la probabilité d'une fonction variable d'aléatoire :

Ce théorème concourt pour calculer la densité de la probabilité d'une fonction variable aléatoire de partir de la connaissance du dérivé de la fonction et de la densité de la probabilité variable de l'aléatoire de laquelle c'est fonction, est eu :. Il est obtenu prenant 3 racines du y=g(x) d'équation et l'inscription le moment peut finalement être exprimée facilement en termes de x et observer cela . Remplaçant le théorème on le démontre.

18) les statistiques de concept de l'indépendance entre les événements, dans un croisillon et un n-n-pla d'aléatoire variable :

Deux ceux aléatoires variables sont statistiquement indépendant si le £ X de P{X, le £ y de Y} = le £ y du £ X} P{Y de P{X}.

19) densité des probabilités d'un g(X deux X aléatoire variable Y et, fonction Y) :

Il est obtenu à partir du dérivé de 2° que l'ordre de la fonction de la distribution combinée F_XY est eu :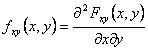

20) coefficient et aléatoire variable de corrélation de la corrélation, cas dans quelle indépendance elle coïncide avec le scorrelationship :

Le coefficient de corrélation de deux X et Y aléatoires variables vaut la peine où m_XY est le covarianza et vaut la peine .

Deux ceux aléatoires variables sont ledit scorrelate si E[XY ] = E[X]E[Y ], la relation qui a remplacé dans la prolongation de covarianza qui pour le scorrelate variable le covarianza et le coefficient de corrélation est nul.

Deux ceux aléatoires variables sont ledit indépendant > f_XY = f_X(x)f_Y(y).

Vous vous notez que le scorrelationship indique l'absence d'une cravate linéaire entre la variable deux tandis que l'indépendance indique l'absence de n'importe quel type de cravate entre la variable deux ceux, donc l'indépendance implique le scorrelationship mais pas le viceversa à moins que dans le cas de gaussien aléatoire variable.

21) transformation d'un croisillon d'aléatoire variable ; pour démontrer le théorème fondamental et pour décrire l'utilisation du membre variable des corps auxiliaires de l'armée des femmes afin d'obtenir la fonction de la densité variable d'une fonction de 2 ceux aléatoires :

Si on a 2 fonctions variables aléatoires d'un tel Z et W que Z = f(X, Y) e W = g(X, Y) alors le théorème fondamental décrit comme obtenir pour des moyens du Jacobiano la fonction combinée de densité de probabilité. est eu, au moyen d'opportun choisi d'un membre variable du bidon auxiliaire de corps de l'armée des femmes comme exemple soit calculé la densité des probabilités variables de la somme de 2 ceux aléatoires.

22) Parlare au sujet des transformations linéaires d'un porteur aléatoire et au sujet du gaussien multivaried un :

Un porteur aléatoire est un tel porteur celui-là n'importe quelle combinaison de ses membres détermine un gaussien aléatoire variable.

23) Ricavare la transformation linéaire qui laisse rendre les membres du milieu un porteur aléatoire gaussien à l'incorrelate de nulle de valor et avec la matrice assignée de covarianza :

24) la courbe de la régression d'un aléatoire variable sur un autre : la propriété produit d'eux, caisse particulière d'un croisillon conjointement de gaussien aléatoire variable :

L'ébauche de l'intégrale qui définit la valeur prévue de Y a conditionné à X pensé comme la fonction de j(x).

25) la vie d'un système ; fiabilité ; fréquence conditionnée des pannes et de ses cours typiques ; interprétation en termes de fréquence relative :

La vie d'un système est l'intervalle de temps que des passages entre la mise dans la fonction et la première infraction, il est décrit d'aléatoire variable le X, sa fonction de la distribution F_X(t) est la probabilité en panne cette le système avant le moment t tandis que l'inverse est la probabilité que le système fonctionne au moment t et s'appelle la fiabilité.

la valeur prévue de la vie du système s'appelle MTBF et caractérise exactement la période moyenne de l'opération sans pannes d'un système. Elle vient a finalement décrit la fréquence conditionnée par préceptes des pannes, conditionnée exactement au fait que le système a fonctionné jusque 2'au temps t. Les cours possibles de la fréquence conditionnée des pannes sont : constante, avec la mortalité infantile, usure, dans la baignoire.

26) cravate entre la fréquence conditionnée des pannes et la fiabilité ; valeur prévue du taux les pannes :

les préceptes ont conditionné la fréquence des pannes, conditionnée exactement au fait que le système a fonctionné jusque 2'au temps t. La valeur prévue de la vie d'un système est égale à la somme des fiabilités simples des sous-ensembles desquels elle se compose.

27) la densité conditionnée et la densité de bivaried le son gaussien de probabilité :

28) le concept du champion aléatoire ; définition de la moyenne du champion ; valeur et désaccord prévus de la moyenne du champion :

Un champion aléatoire est avec de n i.i.d. variable extrait à partir seulement d'aléatoire variable un X, la moyenne du champion ou la collection moyenne d'échantillons est décrite 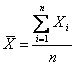de la relation, sa valeur prévue coïncide avec la valeur prévue h de la population tandis que son désaccord avec le désaccord de la population mais de l'uniforme pour n.

29) la densité des probabilités variables de la somme de 2 ceux aléatoires dans le cas général et le cas de l'indipendenza. :

Dans le cas de l'indépendance il est donné du convoluzione des 2 fonctions variables de la densité de deux les aléatoires tandis que la fonction caractéristique est égale au produit des deux fonctions caractéristiques.

30) convergence quadratique à la moyenne et convergence dans la probabilité : définitions et raccordement entre les deux convergences :

La convergence quadratique à la moyenne est donnée de la relation.

La convergence dans la probabilité à la place est donnée de la relation .

La relation entre les deux est que si X_n converge alors à c quadratique à la moyenne elle converge à c dans la probabilité pendant qu'elle est obtenue appliquant l'inégalité de Markov.

31) c aléatoire variable² : statistiques de définition et d'utilisation :

La propriété de c² sont suivante :

) si X sont un C² avec des degrés de m de liberté puis Z = X Y sont un C² avec des degrés de liberté de m n.

b) la somme des places des normes indépendantes gaussiennes de n est un C² avec des degrés de liberté de n.

c) Un C² avec 2 degrés de liberté est une densité exponentielle.

32) distribution de la moyenne et de la collection de désaccord d'échantillons :

La collection moyenne d'échantillons est 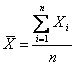lui a la valeur prévue par égale h à celui-là de la population et du désaccord . La collection de désaccord d'échantillons est , sa valeur prévue s'avère est égale au désaccord de la population. Un résultat important est que la variable l'aléatoire est distribuée comme un C² avec des degrés de la liberté n-1. Pour des valeurs il vous élève de n que la collection moyenne d'échantillons suit la loi normale approximativement.

33) décision binaire avec l'observation simple : les concepts produisent d'eux et de l'essai de Neyman - Pearson, avec la démonstration relative :

Une décision binaire quand dans l'espace de lui les marque S sont 2 les marque, à chacun d'eux est eue est l'associée des 2 cloisons de l'espace des observations de Z et doit est prise une de 2 décisions d₀ ou d₁ . L'erreur du type 1° est la probabilité qui les marque était S₀ mais il vient la décision incorrectement prise d₁ , est indiqué avec à et c'est ledit niveau d'importance de l'essai. L'erreur du type 2° est la probabilité qui les marque était S₁ mais il vient la décision incorrectement prise d₀ , est indiqué avec b et son inverse P = 1 - la puissance de b de l'essai est dite.

34) théorie de la décision et du critère de Neyman - Pearson :

On lui propose de partager l'espace des observations pour s'associer des éléments à l'espace des décisions. Le critère de Neyman Pearson mène à l'endroit d'une règle de décision à la laquelle diminue b ayant fixé . En bref on s'applique à la méthode de multiplicateurs de Lagrange essayant entre toutes les régions pour lesquelles le niveau d'importance de l'essai est celui à ₀fixé , celle-là qu'il maximise la puissance de l'essai b . On constate que le rapport de verosimiglianza est plus grand du multiplicateur l choisit d₁ choisit autrement d₀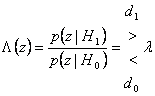

35) théorie axiomatique : Illustre la différence entre l'estime de Bayes et celle-là pas de Bayes ; elle est exemplifiée au cas de l'affette de mesures des erreurs :

Dans le classique d'approche le paramètre q de la distribution f_X(x,q) est vu comme une constante, incognito mais determinist. Dans les statistiques de Bayes incognito le paramètre q est vu comme une réalisation d'un F aléatoire variable .

36) génération de pseudo - accidentel avec la distribution assignée laissant des nombres pseudo - uniformes accidentels de nombres dedans [ 0.1 ] :

Si X sont un un aléatoire variable avec la distribution F(x) puis U = F(x) c'est uniforme distribué dedans (0.1) avec assez la distribution de F(x) donc pour s'appliquer le F^-1(u) à chaque u concernant l'ordre des nombres accidentels avec la distribution uniforme dedans (0.1).

37) décrivent le bâti Karl de méthode :

C'est une méthode basée sur un prélèvement accidentel, en bref une expérience aléatoire est répétée des temps de n et on l'estime la moyenne de s'avère obtenu à vous. La méthode est employée est pour les statistiques d'applications qui pour des applications de determinist. Elle est employée comme exemple dans le calcul des intégrales pour lesquelles les deux méthodes suivantes sont disponibles :

) par le riscalamenti elle est faite de la manière d'intégrer entre 0 et 1. L'intégrale s'avère être la valeur prévue de la fonction g appliquée à un uniforme variable dans (0.1) extraire donc quelques champions, l'intégrale est caractérisée de leur collection moyenne d'échantillons.

b) 2 uniformes variables sont produits dedans (0,1) u et v et pour chaque valeur du u il est commandé si v sont plus petits du g(u). Incognito l'intégrale donc est donnée du rapport entre le nombre d'essais dans lesquels le g(u de £ de vi) et le nombre d'essais.

38) construction des priseurs avec la méthode de moments :

La méthode de moments consiste en égalant les moments de la fonction de la distribution célèbre avec les évaluations de moments à vous

39) estime de paramètre avec la méthode de verosimiglianza maximum. Propriété des priseurs du verosimiglianza maximum :

La méthode de verosimiglianza maximum est basée sur prendre cette valeur de q que plus de verosimilmente qu'il a donné l'endroit aux données observe à vous. Cela en bref se produit dérivant concernant incognito le paramètre la fonction de verosimiglianza qui est la densité du porteur aléatoire du f(X de championsde I , q) pensé comme la fonction de q. Ils sont des priseurs qui pour de petits champions prennent des exécutions insuffisantes, alerte polarise en fait à vous et avoir le grand désaccord, avec l'augmentation de du nombre de champions qu'elles diminuent est la polarisation qui le désaccord et la fonction des bouts droits de distribution à les gaussiens.

40) statistiques de Pearson et l'essai de la qualité de l'adaptation entre une loi théorique et un empiricist de loi :

L'essai a la portée pour établir si un modèle théorique de données adapté aux données efficacement est trouvé à vous, ou si deux ensembles de données il les éprouve ils peuvent être décrits du même modèle. L'hypothèse basse est que les probabilités des événements de m_{à I} sont égales aux valeurs données par m p_0i . Les statistiques qui s'emploie 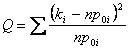est obtenues considérant que les binomiales peuvent être rapprochées d'une normale.

41) statistiques de Pearson et l'essai de c² :

Les statistiques de l'essai de Pearson 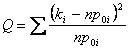se prêtent mal à l'endroit du percentile q₁ alors pour des valeurs élève à vous de n que la distribution des statistiques vient rapproché avec un C² avec des degrés de la liberté m-1 puisque la cravate est régnée , l'hypothèse basse vient rejeté si la valeur 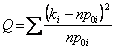des statistiques est plus grande du percentile c²₁(m-1).

42) la méthode des moindres carrés : interprétation, statistiques et predittiva de determinist. :

On doit caractériser une fonction j (x)que meilleur adapté en second lieu un critère a prédéfinie à avec des points donnés. La méthode consiste en déterminant les paramètres l _ide m du modèle j(x) de sorte qu'elle s'avère minimal l'erreur quadratique .

Interprétation de Determinist :

Croisillons (x_i , yi) sont des croisillons des nombres célèbres. Supposer à rapprocher avec un un bx droit de y=a afin de déterminer à et b autre ne doit pas être fait à cela pour diminuer l'erreur quadratique que c'est uguagliando obtenu à 0 le respect de dérivés à à et considérer b.

Statistiques d'interprétation :

Abscissas X sont des nombres célèbres, alors que les formeurs que y sont les valeurs aléatoires vous observent de n Y variable de la valeur prévue E[Y] = j(le xi).

Interprétation de Predittiva :

C'est les abscissas que les formeurs sont les valeurs vous observent d'aléatoire variable.