Théorie des fonctions d'un complexe variable

1) succession convergente :

La succession {z_n} est ledit convergent à la limite z si " et > 0 $ un N(indexet) pour partir de ce que tous les éléments z_n de la succession satisfont l'inégalité |z - z_n| < et pour n > N(et).

 

2) état nécessaire et suffisant de sorte que {z_n} converge est qu'ils convergent simultanément {_{à n}} et {b_n} :

 

3) succession limitée :

Une succession est limitée si $ un tel nombre positif M qui l'" élément z_n ? {z_n} il vaut la peine l'inégalité |z_n| < M

 

 

4) de chaque succession limitée on peut être subsuccession convergent extrait  :

Si {z_n} il est limité alors ils sont également roide S on a que z nord-estS Imz _n donc choisissant un un nopportun _k que _{le nk du nk}Im z du roiz converge.

 

5) Critère de Cauchy :

La succession {z_n} est convergente > " et > 0 que un N(index peut être trouvéet) tels que |z_n - z_m| < et pour le ³ N(de n,met)

le ž   si z_n il est convergent, parce que 2) les vraies successions _{à n} doit converger également et b_n et donc bidon de $ N ₁ dessus ils soient appliqués le critère de Cauchy et être dit qui " et >0(et) tels que " n,m > N₁(et) est eu cela |_{à n} -_{à m}| < et / 2 et celui

" et > 0 $ de N₂(et) tels que " n,m > N₂(et) sont eus cela |b_n - b_m| < et / 2. N(de choixet) = le max(N₁(et), N₂(et)) on l'a que pour le n, m plus grand de N(et) est eu |z_n - z_m| < et .

?   Il peut observer que le module |z_n - z_m| est plus grand sûr du module de la différence des vraies pièces ou du module de la différence des pièces imaginaires, donc de l'ha |_{à n} -_{à m}| < et e |b_n - b_m| < et et donc {_{à n}} et {_{à m}} est les successions convergentes et donc aussi {z_n}.

 

6) succession indéfiniment croissante :

Une succession {z_n} indique indéfiniment l'augmentation si " le nombre positif R existe un index de N à partir de ce que les limites de la succession satisfont la condition |z_n| > R pour le ³ N de n.

 

7) point à l'infini :

C'est le point que chaque succession croissante converge indéfiniment.

 

8) définition de point à l'infini au moyen de la projection stereographic :

Les images que le plan complexe correspond au plan xy de R³ et considère la circonférence d'unitaire de faisceau centré d'origine, la transformation bonne T s'associe à chaque point de point complexe de plan de sphère qui s'avère de l'intersection de la même sphère avec la combinaison du point avec le Polonais du nord, une telle intersection s'avère dans Polonais du nord si le point est externe à la sphère tandis que Polonais Du sud est dedans si le point est intérieur à la sphère, puits si nous avons une succession des points que qui sur la sphère s'étire au Polonais du nord, alors la transformation inverse T^-1 s'étend au point aux infini.

 

9) point intérieur :

Un point z indique le point intérieur d'ensemble et si le son complètement contenu dedans existe ensemble autour et

 

10) avec ouvert :

C'est de seuls points intérieurs constitués d'une intégralité.

 

11) avec relié :

Il est avec dans quels 2 pris n'importe quel concerner se dirige à lui, ils peuvent être joint au moyen d'un poligonale dont les points sont contenus dedans avec mêmes.

 

12) dominion :

Ébauche ouverte et reliée de avec.

 

13) point de frontière :

Un point z indique que le point de frontière pour et si dans chaque son autour il y a il est piqué d'ensemble et cela de sa complémentaire.

 

14) dominion clôturé :

L'ébauche de l'union d'un dominion avec le son est visée de la frontière.

 

15) dominion limité :

Ébauche d'un dominion situé complètement à l'intérieur d'une circonférence de faisceau fini.

 

16) limite d'une fonction complexe :

Le nombre W₀ indique la limite de valeur du f(z) de fonction dans le point z₀ si " et > 0 un d peut être trouvé > 0 tels que pour tous les points z qu'ils satisfont la condition 0 < | z - z₀ | < d il vaut la peine le disuguaglianza |f(z) - W₀| < et .

 

17) continuité d'une fonction complexe :

Le f(z) de fonction est continu dans le point z₀ si " et > 0 un d peut être trouvé > 0 tels que pour tous les points z qu'ils satisfont le condizione | z - z₀ | < d il vaut la peine le disuguaglianza |f(z) - f(z₀)| < et .

 

18) dérivé de fonction d'un complexe variable :

Si cette limite existe finissait alors la limite qu'elle indique dérivé du f(z) de fonction concernant le complexe variable z dans le point z₀ .

 

19) interprétation géométrique du dérivé complexe :

En outre dans le cas complexe le dérivé est vu comme le rapport entre la variation de l'image Wde D et la variation du dominion zde D, avec la limite pour qui s'étend à 0, ne traitant pas avec nous du fait qui est le dominion que l'image est bi-dimensionnelle, a donc qui est ébauche d'un nombre complexe au dont l'argument est donné de la différence entre l'argument du numérateur et l'argument du dénominateur mais de ces arguments quand Dz®0 est égal aux tangentes aux courbes respectives dans l'image et le dominion et cela est est par à l'angle inclus entre le vrai axe et le porteur Dz ou différencede D W à cette est même pour le chaque un autre point passant pour z₀ . Cette propriété est dite de la conservation des angles.

La propriété de l'expansion linéaire, est obtenue faisant à la place le module du à partir de ce qu'elle trouve cela et donc k caractérise le coefficient de la balance du similitudine.

 

20) définition de fonction différentiable dans le sens complexe :

f(z) il est différentiable dans z₀ s'il respecte l'équation suivante :

étant e .

21) f que c'est analytics dans z₀ > f est différentiable dans z₀ et il est eu :

ž                 Deriva directement de l'analytics de définition de fonction

? Assez pour prendre la définition de differenziabilità

porter le f(z₀) au premier membre et puis se diviser pour (z-z₀) tirer profit de cela est eu la définition de derivabilità qui est seulement eue dans le cas que f est analytics.

 

22)Se le f(z) = l'u(x de fonction, y) le v(x, y) est derivabile dans le point z₀ = x_{0 0 qu'}iy alors dans le point (x₀ , y₀) existe les dérivés partiels de l'u(x de fonctions, y) et v(x, y) concernant x et y variable et le sussiste la relation de Cauchy - Riemann

a) u_X = v_y b) u_y = - v_X

Pour la définition une fonction est analytics s'il est différentiable et mais du repos est eu que donc et remplacement analogue dans le précédent les conditions de Cauchy-Riemann sont obtenu juste.

 

23) analytics ou olomorfa de fonction ou pour régler :

Le f(z) de fonction indique l'analytics, olomorfa ou pour régler s'il est derivabile dans tous les points du dominion et son dérivé est continu.

 

24) f c'est analytics  > les dérivés partiels de l'u(x de fonctions, y) et v(x, y) ils existent, ils sont continus et pour eux ils valent la peine les conditions de Cauchy - Riemann :

25) théorème de Gouisal :

Si f il est allumé analytics ouvert avec puis f ? Là

 

26) fonction entière :

Ébauche d'une fonction d'olomorfa en tout le C.

 

27) à application conformée :

L'ébauche de la transformation d'autour du point z₀ dedans autour du point W₀ a effectué de l'analytics de fonction

W = f(z), ayant dans le point z_{les 0} propriétés de la conservation des angles et du costanza de l'expansion linéaire.

 

28) la forme différencie pour les tracer :

W = A(x, y)dx B(x, y) B dy, continu complexe sur W .

 

29) théorème de gauss - vert :

C'est W ouvert (limité) et ¶parfois un tel W régulier qui W ? Là(w) ? C(W)

 

30) la forme les différencie écluse :

Une forme les différencie que W indique que l'écluse s'il est exact et derivabile, parce que une forme les différencie l'écluse est doit_y = B_X .

 

31) si W est un dominion simplement relié, ž

W que c'est chiusa > W est exact 

le ž si W il est écluse puis se décomposent F = 0 au lequel est_y = B_X donc appliquant le théorème du vert de gauss à l'effet contraire a et est l'une des définitions de W exactes qui est que son intégrale le long d'une distance fermée est nulle.

?   Si W il est exact puis il admet que une fonction les améliore un tel U au lequel = U_X et B=U_y dérivant avant que le respect à y et le deuxième respect à x et tirer profit du théorème de Schwarz sur l'égalité des dérivés mélangés, soit eu

Àon a _y =U _xy =_yx de U =B _X et donc que W il est écluse.

 

32) formule de vert dans le cas complexe :

Être lui est eu qu' a=f trompeur e B = si donc doit partir du résultat valide dans le vrai domaine

 

33) découpe clôturée :

L'ébauche d'une écluse régulière de courbe prive parfois des intersections de voiture.

 

34) théorème de Cauchy :

Dans un dominion simplement relié l'intégrale prolongée du f(z) est définie un ž de f(z) d'analytics de fonction à chaque découpe fermée G, complètement contenue dans le dominion de G, est égale à 0.

après avoir appliqué les conditions de Cauchy Riemann puisque f il est analytics.

 

35) seconde formulation du théorème de Cauchy :

Si le f(z) de fonction est l'analytics dans un dominion simplement relié a limité une découpe régulière parfois C et est continu dans le ž fermé du dominion G l'intégrale du f(z) prolongé de fonction à la frontière du dominion de G qu'il est égal à zéro.

 

36) intégrales de Fresnel  :

Intégrant sur un circuit fermé, les 2 vraies intégrales sont obtenues

 

37) formule intégrale de Cauchy :

Si le f(z) il est long analytics en dedans et frontière C d'un ž simplement relié de la région R

Vous vous notez en fait que le f(z) il est ovunque d'analytics sauf que dans z = à, donc l'intégrale soit indépendante du circuit fermé au lequel enferme, cela est l'intégrale le long de C est égale à l'intégrale effectuée le long d'une circonférence de faisceau et centré dedans c'est-à-dire, un parametrizzazione pour le è de G z = à et et ^q et donc dz = et et le remplacement ^{de q} sont obtenus

et passant à la limite pour et ® au 0 et isolant le f(a) obtient la thèse.

 

38) théorème du milieu de valor :

La valeur de f est olomorfa de f dans le dominion au ž dans un point de à est égale à la moyenne des valeurs de f sur une n'importe quelle circonférence centrée dans celle point contenu et, avec à son intérieur, dans A :

On le démontre au congé de la formule de Cauchy où admettre ce z = au roi que ^{le q} est un parametrizzazione du dz = de la colère ^q du cercle C haet remplaçant dans l'intégrale il est obtenu .

 

39) principe du module maximum :

C'est analytics de f(z) en dedans et longue une ligne simple ž de l'écluse C le maximum de |f(z)| on le trouve moins le long de C que le f(z) que ce n'est pas une constante.

La fonction est continue sur compacte admet donc un maximum, suppose pour l'absurdité qu'un tel maximum est assumé dans un point à l'intérieur au dominion, s'appliquant le théorème de la moyenne sur un cercle centré dedans à la volonté ayez donc la valeur du f(a) est M juste et est égal au milieu de valor, mais pour les points de la circonférence elle doit avoir elle-même |f(a)| > |f(a au sujet du q)| alors la valeur moyenne M ne peut pas être rattrapée et ceci implique que c'était une absurdité et que donc le maximum vient a supposé sur le bord du cercle. Évidemment donc si le maximum est intérieur au dominion, la fonction ne peut pas cela être constant à l'intérieur de le même, si n'est pas donc alors la fonction assume le maximum sur le bord d'ensemble.

Nous avons dans une telle manière avons démontré que la fonction est constante à l'intérieur du cercle du centre à, afin de prolonger le résultat à tout le dominion, les prises à à n'importe quels point et lui est combiné avec une ligne, dopodichè que un point est pris sur cette ligne qui est à côté du bord du premier cercle et on le suppose comme le centre du nouveau cercle sur lequel répétant les considérations précédentes.

 

40) Corollario du principe du maximum :

C'est à l'olomorfa un dominion limité et f dedans à, il continue dedans à , et pas ž de costante la fonction z® |f(z)| il assume le maximum sur la frontière de à.

 

41) théorème du module minimal :

C'est analytics de f(z) dans et suivant la ligne simple l'écluse C et est le ¹ 0 de f(z) dans le ž de C |f(z)| il assume son long minimum C.

f(z) c'est analytics dans C et puisqu'il n'a pas des zéros dans un tel dominion qu'il suit que specularly qui est également analytics dans C donc étant en conditions de la validité du théorème du maximum une telle fonction de module peut seulement admettre le maximum sur la frontière C et donc |f(z)| il peut seulement assumer le minimum sur la frontière C.

 

42) évaluation du dérivé d'un employé intégral d'un paramètre :

Le dérivé de l'intégrale est égal à l'intégrale de l'integranda dérivé de fonction concernant le paramètre.

 

43) lemme de dérivation sous le signe de l'intégrale :

Elle est à un dominion et à un G un arc de courbe orientée, et à un j une fonction définie et continue sur le ž de G que la taille définit dedans \ G une fonction d'olomorfa, et son dérivé a l'expression

d'ailleurs f qu'il possède dérivé de chaque ordre et est eu.

Partie de l'intégrale de Cauchy , l'integranda de fonction est analytics concernant z et son dérivé partiel se rappelle donc que l'intégrale de Cauchy est un employé intégral du paramètre z, est eu qui son dérivé est égal à l'intégrale du dérivé concernant le paramètre de l'integranda de fonction.

 

44) théorème de tailleur :

C'est f est analytics à l'intérieur du cercle C avec le centre dedans au ž la série de tailleur de f dans le point : converge au f(z).

C'est z par point intérieur à C et un cercle C ₁est construit qu'il joint z mais il est contenu en C et les les deux les cercles sont centraux à vous dedans à. La valeur du f(z) donc est indiquée de la formule intégrale de Cauchy mais du repos elle est eue 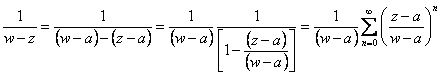à condition que c'est le rapport plus petit de 1 ossia |z-a| < |w-a| donc à l'intérieur du cercle C₁ . À ce point il est multiplié pour f(w)/2pi, l'intégrale une sur C₁ obtenant donc au premier membre le f(z) tandis qu'au membro 2°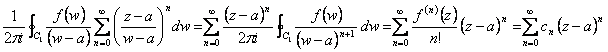

 

45) unité du développement en série de puissances :

C'est olomorfa de f dans le dominion à z₀ ? À, e il est eu, dedans autour du žde z ₀

 

46) inégalité de Cauchy :

Si le f(z) il est long analytics en dedans et le cercle C r de faisceau et centre dans z = à, étant M : |f(z)| < M

La partie de la formule intégrale du dérivé de Cauchy duquel prenant au module et le maggiorando l'intégrale curviligne avec la longueur de la circonférence 2pr multipliée pour le maximum M chargent de la fonction sur la circonférence 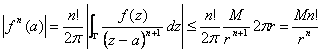est obtenue.

 

47) théorème de Liouville :

Si pour tous les points d'entier lentement le complexe un, f(z) il est analytics et f(z) limité de ž il est constant.

Il est obtenu à partir de l'inégalité de Cauchy prenant n = 1 ha et étant le dérivé nul avant que " z qu'il suit que la fonction doit être constante.

 

48) théorème fondamental d'algèbre :

Chaque polynôme du ³ 1 du degré n elle possède au moins un zéro dans le plan complexe.

Nous admettons pour l'absurdité que le polynôme le P(z) n'a pas des zéros, donc c'est analytics pour n'importe quels z et lui s'avère également être limité dans le module par ¥® de z donc pour le théorème de Liouville que la fonction doit être constante, mais un polynôme il ne peut pas être être constant du ³ 1 du degrén et donc le polynôme est tombé en contradiction, par conséquent doit admettre un zéro au moins, sera démontré alors que le n° des zéros il est exactement n.

 

49) théorème de Laurent :

Si le f(z) il est analytics en dedans et long concentré de 2 cercles du faisceau centre respectifs de R₁ et ₂R et à nous dedans au ž

escroc

DÉMONSTRATION DE L'EXISTENCE

Nous caractérisons 2 circonférences du faisceau R₁ et ₂contenus R <R _{un 1} à l'intérieur de la couronne circulaire et au point intérieur z aux 2 circonférences, alors la valeur de la fonction dans ce point z est donnés de la formule de Cauchy, parce que 1° la limite est raisonné donc quant à la série de tailleur caractériser la somme d'une série convergente 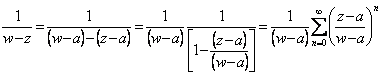a donc avec .

Le rassemblement analogue pour 2° 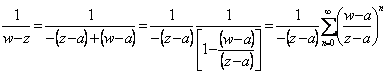le membre est obtenu contre . Puisqu'à l'intérieur de la couronne circulaire la fonction est analytics, le ž le théorème de Cauchy peut être appliqué et donc l'intégrale est indépendante de la distance particulière, en suit que les 2 solutions peuvent être groupées dedans avec .

DÉMONSTRATION DE L'UNICITA '

On le suppose d'avoir 2 séries qui diffèrent pour un coefficient simple, multiplie tous les deux pour (z-z₀)^{- m-1} et si de il y a l'intégrale le long d'une circonférence comportée dans avoir l'anneau de l'olomorfia et le centre dans z₀ , remplaçant à ce point z = roi^{le q} trouve des 0 intégrales qu'il vaut la peine si le ¹mde n tandis qu'il vaut la peine 2psi n=m, après que tout dans chaque développement il y ait une limite non nulle simple et soit égal pour les deux séries cela coïncide donc.

 

50) Singolarità dismissable :

Si une fonction au solénoïde une valeur n'est pas définie dans z = à, mais lui existe dit que z = au singolarità dismissable est un.

 

51) si le f(z) il est analytics limité et dans un dominion qui exclut z₀ , dirigez alors z₀ est un point singulier dismissable :

Affinchè z₀ est un singulier dismissable de point, les coefficients de la partie principale de la série de laurent doivent être tout les nuls, qu'on le démontre écrivant c_n en termes d'intégrale et effectuant le compte usuel de possession de maggiorazioni que la fonction est limitée cet is!f(z)| < M, remplaçant alors (â "z ₀de z) = roi^{le q} et faisant la limite pour r®0 obtient 0 comme intentionnel.

 

52) Polonais :

Si une fonction au solénoïde une valeur a un poteau dans z = à, le ž et le nombre de limites actuelles dans la partie principale de la série de Laurent correspond à l'ordre du poteau.

53) si le point z₀ est un poteau du ž de f(z) d'analytics de fonction pour z®z₀ le module du f(z) de fonction se développe infiniment, indépendamment de la manière de laquelle le point z il s'étend au point z₀ :

Assez pour écrire le développement de Laurent au congé exactement du â?"m de limite supposant un poteau de l'ordre m, se rassemblant dans la partie principale (z-z₀)^{- m} ont limité où j le (z) est analytics et dedans autour de z₀ et donc de limite (z-z₀)^{- m qu'} il commande et il pousse vers infini le f(z) pour z®z₀ .

54) si un f(z) de fonction, analytics dedans autour d'un son z d'isolement par point singulier₀ se développe infiniment dans le module indépendamment de la manière de laquelle le point z ₀ du point z s'étend au ž du point z ₀ il est un poteau du f(z) de fonction :

On considère la fonction qui les bouts droits à 0 pour z®z₀ est donc limité et donc pour lui z₀ sont un singolarità dismissable et peuvent donc être écrits où j(z) est une fonction un tel analytics que le ¹0 de j(z ₀) a donc que c'est la définition du poteau de l'ordre m.

 

55) Singolarità essentiel :

Si le f(z) chaque singolarità est une fonction au solénoïde un ž de valeur qui n'est pas d'un poteau d'un zéro est un singolarità essentiel, en particulier si z = à la partie principale du développement de Laurent est un singolarità essentiel alors a un nombre infiniment de limites.

 

56) fonction de meromorfa :

Une fonction indique le meromorfa si c'est analytics dans tout le plan excepté un nombre fini de poteaux.

 

57) Theorem di Casorati - Weierstrass :

Pour le chaque et> 0 dans lequel autour d'essentiel un point singulier z₀ du f(z) de fonction par point z ₁ dans lequel la valeur de la fonction existe au moins f(z) il diffère moins d'un nombre complexe B arbitrairement assigné dans l'ordre qu' et.

Nous supposons pour l'absurdité qui existe autourde z ₀ dans lequel on le a lieu que , puis la fonction est limitée et donc le point z₀ est un point singulier dismissable du jy

cil donc pour le théorème précédent, peut être écrit venu et gagner le f(z) du est obtenu mais si ce développement m=0 caractérise un point régulier pour le f(z) caractérise autrement un poteau de l'ordre m et de non un singolarità essentiel comme le théorème a exigé.