Série complexe
Série Numérique
1) série convergente :
La série indique le convergent si la
succession {S n}de
ses sommes partielles est convergente, dans un tel cas que la limite
de S de la succession {Sn}
indique la somme de la série .
2) n-esimo de repos de la série :
Ébauche de la série 
.
3) Critère de convergence de Cauchy :
La série est convergente > " et > 0 un index de N peut être trouvé tels que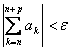 
par ³ Nde n.
4) absolument série de convergent :
Si la série à de vraies limites 
est
alors convergente également la série qui est dans
ce cas-ci absolument convergente .
5) Critère de convergence de d'Alembert :
La série est convergente si, commencer d'un
index de N, ³ N de n 
vaut la peine relation le ".
6) Critère de convergence de Cauchy :
La série est convergente si, commencer d'un
index de N, ³ N de n 
vaut la peine relation le ".
Série de fonctions
7) convergence ponctuelle :
La série de fonctions 
indique le
convergent dans son dominion si la série numérique au parent il
converge " z qui est si " z et pour chaque nombre positif et un index de N peut être
trouvé tels que 
pour n > N .
8) convergence uniforme :
La série d'uniforme de fonctions
indique le convergent dans son dominion si la série numérique au
parent il converge " z qui est si " nombre positif et peut être trouvé un N(indexet) tels que " n > N(et), chaque pour z concernant le dominion.
9) Critère de Weierstrass de total de convergence :
Si dans un dominion les modules des limites de la série
de fonctions sont ovunque accru des limites
d'un numérique absolument convergent de série la série elle converge uniforme dans son dominion.
10) Critère de Cauchy :
L'état nécessaire et suffisant pour la convergence
uniforme de la série est que " et > 0 un N(existset) tels que 
la relation est vérifiée simultanément dans tous les
points du dominion pour le ³ N et " m de n.
11) théorème de Weierstrass sur la propriété de la série convergente uniforme :
Si les fonctions un(z) sont continues dans le dominion de u et si la série converge uniforme dans ce dominion au f(z)
de de f(z) de fonction
également elle est continue dans le même dominion.
12) théorème d'Abel ou Cauchy - Hadamard :
Si la série de puissances 
converge
dans un ¹ z0 du point z1 , elle converge absolument également dans un tel point z
cela |z-z0| < |z1 - z0| ; d'ailleurs la série converge uniforme
en chaque cercle |z-z0| £ r de faisceau r < |z1 - z0|.
En étant la série convergente en sestermes de z 1 alors
étirez au zéro pour le bidon®général de limite de ¥ de n donc qui est soit
augmenté d'un M constant 
et donc 
est eu mais nous sommes intéressés de voir si la série
pour un tel point converge absolument z cela |z-z0|<|z1 - z0| donc nous prenons le module
de la série 
de puissances mais est une série géométrique de raison q<1 et donc
la série indiquée est convergente donc pour le critère de la
comparaison converge absolument. Afin de démontrer la
convergence uniforme on emploie le critère de Weierstrass qui
visionne le maggiorazione avec une série numérique convergente qui
comme exemple il peut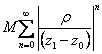 
être r < |z1 - z0| .
13) la série convergente de puissances
au f(z) est une en cercle de convergence D(z0 , R)
le f(z)
de est
l'analytics et le f '(z) = 
14) théorème du passage de la limite sous le signe de l'intégrale :
Donné une série de fonctions continues convergentes uniformes et à l'u(z) dans un
dominion de D
la courbe régulière parfois contenue du " G
dans D est eue 
Elle s'observe que la différence entre
l'integrandi deux est égale au n-esimo de repos et à être
l'uniforme convergent de série, le bidon qui est soit augmenté 
où L est la longueur de la courbe le long de
laquelle l'intégrale, donc 
est eue et donc il y a
l'égalité entre les deux limites.
