Théorie de la résiduelle

1) résiduel :

Ébauche du coefficient_{à -1} de la série de Laurent

 

2) formule afin de calculer le résiduel dans z = à le moment où à lui est un poteau simple :

Il est obtenu pour partir du développement en série de Laurent, se multipliant pour (le z-a) et en faisant à la limite toutes les limites soyez le coefficient décommandé c _-1d'ad.eccezione.del .

 

3) la formule afin de calculer le résiduel dans z = à le moment où à lui est un poteau et un f(z) simples est un rapport des fonctions :

Le f(z) le dénominateur a un poteau au lequel est a un zéro dedans et donc il peut être écrit en série de tailleur et d'observer la fonction qu'il constate que le coefficient de est juste

 

4) formule afin de calculer le résiduel dans z = à le moment où à lui est un poteau de l'ordre m :

Si à la série de Laurent de f(z) est un poteau de l'ordre m puis il est : se multiplier par (z-a)^m obtient une série de dérivation de tailleur que m-1 chronomètre et la fabrication de la limite pour z®à est obtenue_{à -1} en fait de quel la formule exigée.

 

5) théorème de le résiduel :

C'est f(z) par fonction au solénoïde une valeur et un analytics à l'intérieur et sur la ligne simple faite eccezion de l'écluse C pour le singolarità à, b, c... à l'intérieur de C que les données résiduelles ont l'élasticité_{à -1} , b_-1 , žde c _-1 ....

Il est suffisant le prendre pour chaque de singolarità contenu dans C et circonférence centrée dans le même singolarità, et observer cela et observer que chacun des intégrales au deuxième membre peut être simplement extrapolée du coefficient_{à -1} de la série de Laurent, en fait est eu .

 

6) résiduel à l'infini :

Résiduel de la fonction le f(z) d'analytics dans le point z = ¥ c'est le complexe égal à la valeur de l'intégrale

 

7)       si le f(z) il est un analytics de fonction dans tout le plan complexe excepté un nombre fini d'isolats singuliers de points à vous entre quel z = ž de ¥ la somme de la résiduelle est zéro.

8) Di Jordanie de lemme :

Si le f(z) de fonction est analytics dans tout le semiplan avançé excepté un nombre fini de points singuliers lui des isolats à vous et lui s'étire à zéro pour |z| ® le respect uniforme de ¥ par q avec le ž du £ p du £ q de W 0 par > à 0 a être Cr 'l'arc de la circonférence du semiplan avançé avec |z| = R.

est eu dont plaçant |f(x)| < m_R X = roi^{i j} e dX = roi de I^{i j} dj ha

et tirant profit que dans [ 0,p/2 ] la sondej > 2j/p il est eu : et donc le lemme est démontré.

 

9) si le f(x) il est une fonction définie sur tout le vrai axe et peut semislowly être prolongé analytiquement au semiplan avançé et dans tels il satisfait les Di Jordanie de lemme et il n'a pas les points singuliers sur le vrai ž $ d'axe  étant z_k les points singuliers du f(z) de fonction dans le semiplan avançé.

 

logaritmica 10)Derivata :

Si le f(z) il est un univoca d'analytics de fonction avec un nombre fini de singolarità dirige des isolats à vous, tous les poteaux dont personne des trouvailles sur la frontière du dominion alors le membre de fonction des corps auxiliaires de l'armée des femmes n'est ledit logaritmica dérivé

 

11) logaritmico résiduel :

L'ébauche du résiduel de la fonction le membre des corps auxiliaires de l'armée des femmes j(z) est estimée à vous dans des ses têtes de singolarità.

 

12) valeur de logaritmico résiduel dans un zéro d'ordre k du f(z) de fonction :

Le logaritmico résiduel est égal à l'ordre du zéro.

On le démontre en observant que si à est un zéro de commande n pour le f(z) puis dans son autour bidon lui-même soyez écrit le f(z) = (z-a)ⁿ f₁(z)

vient utilisé dans le calcul du membre 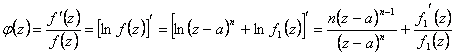de fonction des corps auxiliaires de l'armée des femmes devenant plus simples et se rappeler que le résiduel est égal au coefficient de (z-a)^-1 obtient qu'il vaut la peine n qui est est égal à la variété du zéro.

 

13) valeur du logaritmico résiduel dans un poteau de l'ordre k du f(z) de fonction :

Le logaritmico résiduel est égal à l'ordre du poteau pris avec le négatif de signe.

On le démontre en observant que si à est un poteau de la commande n pour le f(z) alors dans son autour bidon lui-même soit écrit le f(z) = (z-a)^{- p} f₁(z)

vient utilisé dans le calcul du membr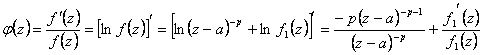e de fonction des corps auxiliaires de l'armée des femmes devenant plus simples et se rappeler que le résiduel est égal au coefficient de (z-a)^-1 obtient qu'il vaut la peine - p qui est lui est égal à la variété du poteau changé du signe.

 

14) théorème de l'argument :

Si le f(z) il est un ovunque d'analytics de fonction dans un dominion fermé G sauf que dans un nombre fini de singulier dirige z_{k qu'} il vous situe à l'intérieur de G. Supponiamo que tout le z_k sont des poteaux et que les annulations de f(z) de fonction pas dans aucun point de la frontière de G du ž du dominion G la différence entre le total de nombre des zéros N et le total de nombre des poteaux de P du f(z) de fonction du dominion de G n'est définies de l'expression .

Le théorème est démontré calculant l'intégrale à selon le membre par le théorème de le résiduel et observant que le logarithme résiduel d'une fonction dans un zéro est égale juste à la variété du 0 et analogue le logaritmico résiduel dans un poteau qu'il est égale juste à la variété d'algebrica du même poteau.

 

15) interprétation géométrique du théorème de l'argument :

Il doit être remplacé à l'intérieur de l'intégrale du théorème de l'argument et pour décomposer le logarithme comme le logarithme du module plus les temps la variation de l'argument de la fonction, a

Est en fait un vrai univoca de fonction donc que la variation de son argument est 0 tandis qu'2° le membre exprime la variation de l'argument qui est le nombre de totaux de tours autour du point w=0 que le point W accomplit quand le point z couvre le bord du dominion dans le sens positif.

 

16) index d'un respect de point à une courbe :

L'index d'un respect de point à une écluse de courbe est le nombre de fois que ceci vient couvert concernant le point.

 

17) théorème de Rouche :

Si le f(z) de fonctions et le j(z) sont analytics dans le dominion fermé G, et sur la frontière de G du dominion de G il vaut la peine l'inégalité |f(z)|_G > |j(z)|Le ž _{de G} le total de nombre de zéros de la fonction F(z) = f(z) j(z) est égal au total de nombre de zéros du f(z) de fonction.

On l'a que le nombre de zéros de la fonction de F(z) est tandis que pour le f(z) de fonction que le nombre de zéros détourne le membre au membre doit constater que la différence entre le nombre de zéros doit être nulle. 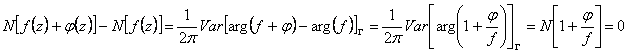est en fait le point eu W = 0 est trouvé extérieurement au circuit couvert de W.

 

18) théorème fondamental d'algèbre :

Un polynôme du degré n qu'il possède dans les zéros complexes du plan n exactement (comptant également leur variété).

On nous observe remplisseur en état de pouvoir s'appliquer au théorème des chapeaux de Rouche à un tel but si e est pris, écrivant le rapport des modules ha, qu'on peut toujours trouver une circonférence d'un tel faisceau de R qu' et donc est eu |g(z)| < |f(z)| donc pour le théorème du f(z) polynôme de Rouche le g(z) possède le même nombre de zéros du f(z) polynôme qu'il a des zéros tous de n dans l'origine.