Gamme, bêta, fonctions de Bessel

Fonctions d'Euler

1) Range di Euler :

ébauche d'une fonction d'olomorfa dans Rez plat > 0.

 

2) formule de répétition :

Elle est obtenue calculant l'intégrale pour des pièces, est eue .

 

3) formule de la factorielle :

Elle est obtenue à partir de la formule de la répétition ; jusqu'à l'alla d'arrivée et au placement dans lui z = 1 le résultat est obtenu.

 

4) la prolongation du G(z) également aux valeurs vous a nié de z :

En gagnant l'iterando la formule de la répétition jusqu'à atteindre le G(z n) est obtenu à selon le membre que une expression multipliée pour le G(z) qui peut donc être estrinsecata, obtient une relation indépendante de n pendant qu'elle peut être remplacement vérifié n = n p, la relation a la validité pour Re(z n) > 0 et présente le singolarità de n polaire.

 

5) qui alliage de relation le G à l'intégrale du gauss :

On se rappelle l'est obtenu avant de remplacerles t=s ² dans la définition du G (z) et après que le ½ soit placé z = et de lui à nous de la valeur de l'intégrale du gauss .

 

6) bêta d'Eulero :

 

7) relation entre le bêta et la gamme di Euler :

On remplace le t=u² dans le G(p) et les t=s² dans le dopodichède G (q) sont multipliés entre d'eux rassemblant les facteurs communs, sont remplacement obtenu dans quels u=rcosq e s=rsenq avec le duds=rdrdq est atteinte l'intégrale où 2 multipliés pour l'intégrale sont justes le b(p,q) ce il peuvent être obtenus remplaçant des t=cos²q .

 

8) formule des compléments :

Elle est obtenue écrivant le b en termes de G donc effectuant la substitution et résolvant l'intégrale qui devient l'intégrale indéfinie d'un polidroma de fonction au moyen du théorème de le résiduel.

Fonctions de Bessel

9) génératrice de fonction des fonctions de Bessel :

On l'a est une fonction d'olomorfa à laquelle une série de Laurent avec des infinites est des finitions associées au négatif et aux infinites d'exposant que vous finissez à l'exposant positif, 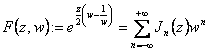qui est où les coefficients _nde J de ce développement sont lesdites fonctions des premières espèces de Bessel.

 

10) valeur des coefficients J_n(z) :

Ils sont obtenus pour partir de la génératrice de fonction

Je peux me multiplier dans combien les deux séries convergent sont absolument eues et le placement du n-m=k qu'il est eu donc est eu .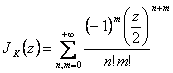

 

11) démontrent la formule le J_{- n} (z) = (-1)ⁿ J_n(z) :

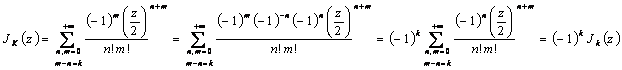est eu.

 

12) l'équation les différencie de Bessel de l'ordre n :

C'est une équation les différencie dans la forme que sa solution est la fonction de Bessel des espèces 1ª de l'ordre n. Il est obtenu dérivant les les deux les membres 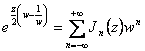du z considérant et considérer W,   est eu : de quel observer que se multiplier ou dividende pour W il est allé pour modifier son coefficient k, il est eu : et donc il est obtenu

J_{n - 1} - J_{n 1} = 2 J '_n. La dérivation concernant W a à la place  de ce qu' et donc elle est obtenue .

Ajouter les 2 relations obtenues est eu et l'augmentant il est eu , au lieu de cela le détournement des 2 relations est eu et la dérivation de lui concernant z est eue et le remplacement pour la dernière fois des 2 dans l'antepenultimate un que l'équation est obtenue les différencie de Bessel .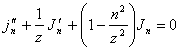

 

13) développement des fonctions trigonometrical en série de fonctions de Bessel :

Il est placement obtenu dans la génératrice de fonction W = et^q l'obtention donc

Estrinsecando est eu

De quel égaler les vraies limites et les limites imaginaires et du placement /2 développements suivantsde j = de p des 2 sont obtenu :

 

14) l'application de l'équation les différencie de Bessel :

On son application est dans l'équation du mouvement d'une membrane circulaire.

 

15)    représentation intégrale des fonctions de Bessel :

Considérer de pouvoir associer à la fonction par série de Laurent, les coefficients c _nde I sont estimés comme exemple avec l'intégrale curviligne et typique de la résiduelle, calculant cette intégrale obtiennent suivre :

On obtient se rappeler que le J_n(z) n'est pas autre que les coefficients d'une série de laurent et de ces derniers sont indiqué de l'intégrale 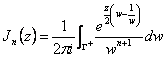et remplaçant le w=e^{le q} le résultat est obtenu.