Fonctions harmoniques
1) fonction harmonique :
Un f : C2® " est ledit harmonique s'il s'avère être solution de l'équation de Laplace Uxx U= 0 yy
2) si D est un simplement relié d'intégralité chaque fonction harmonique dans D admet un harmonica conjugué moins seulement déterminé que celui constant :
3) principe du maximum pour des fonctions harmoniques :
Une fonction harmonique U non constant n'assume aucun maximum de minimal dans le dominion dans lequel il est défini, en particulier si le dominion est une intégralité fermée et limitée, le maximum et le minimum de U sont assumés sur la frontière.
4) décrivent le problème de Dirichlet et la méthode pour sa résolution :
On lui invite à définir l'u(x de fonction, z) satisfaisant l'équation de Laplace Du = 0 dans un dominion de G, qu'il est continu dans le dominion fermé et cela suppose que les valeurs vous assigne sur la frontière de G. La méthode de résolution est suivante :
) on essaye une application cohérente qu'elle transforme le dominion donné en cercle unitaire
b) la valeur de la fonction harmonique au centre du cercle par la formule du valor est milieu déterminé
c) Exprimant la solution en fonction de la variable du départ, le problème est résolu.
5) solution du problème de Dirichlet pour le cercle du faisceau à par la fonction à la laquelle apparaît en condition au bord (j) :
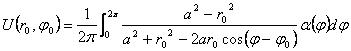
6) solution du problème de Dirichlet pour le semiplan par la fonction à la laquelle apparaît en condition au bord (j) :
![]()
