Théorèmes sur les successions et les séries de fonctions
Successions des fonctions
1) Critère de convergence ponctuelle :
L'état nécessaire et suffisant parce que la succession du funzioni fn converge ponctuellement dedans à est que, fixé et > 0, " t?À N(età,t) tel existe cela : |fn(t) - fm(t)| < et " n, m > N.
2) Critère de convergence uniforme :
L'état nécessaire et suffisant parce que la succession du funzioni fn converge uniforme dedans à est qui, fixé et > 0, existe N(et) tels que : |fn(t) - fm(t)| < et " t? Un " n, m > N.
3) la limite d'une succession d'uniforme convergent limitédes fonctions f n est une fonction limitée :
Partie de la définition de la convergence uniforme |fn(t) - fm(t)| < et si n, m > N après quoi lui est envoyé à n au ¥ et place m = N. À ce point peut employer l'inégalité triangulaire et écrire |f(t)| - |fN(t)| < |f(t) - fN(t)| < et
plaçant et = 1 ha |f(t)| < 1 |fN(t)| et donc le sup de |f| il est limité du sup de |fN|
4) théorème de l'échange des limites
Il est 
uniforme dans le
de A
e 
Je démontre avant que la succession ln vers la droite de l'égale est convergente, nous constaterai que sa limite est l et la même limite sera eue également pour 1° le membre. La convergence est fixée a basé sur le critère de la convergence uniforme, en fait il est eue
|ln - lm| = |l n-fn(t) fn(t) - fm(t) fm(t) - lm| £ |l n-fn(t)| |fn(t) - fm(t)| |fm(t) - lm| < et
étant le module et les modules externes plus petits et pour
des centres ils plus petits et pour l'uniforme de convergence en A. Rimane du donc en solo
pour démontrer que 1° le membre 
afin de faire ce
qui est installent l'inégalité usuelle des limites |f(t) - l| £ |f(t) - fN(t)| |fN(t) - lN(t)| |lN(t) - l| £ 2et |fN(t) - lN| < 3et ,
où pour les extérieurs la convergence uniforme du l a été ntiré profit et pour la limite
il les centre 2ª l'hypothèse du théorème.
5) si la succession des fonctions continues fn converge uniforme sa limite f est une fonction continue.
On le démontre s'appliquant le théorème de l'échange
des limites à la fonction 
.
6) théorème de l'échange de la limite avec le dérivé :
On est succession eue des fonctions fn :® Au l'" derivabili et
) la succession des dérivés {fn'} il converge uniforme dedans (a,b) avec la limite g
b) la succession des fonctions {fn} converge au moins dans un point t0 ? (a,b)
le
également la
succession fn converge
l'uniforme dedans (a,b) et il est eu 
) il doit démontrer que {fn} il converge uniforme, cela est est
respecté l'état nécessaire et suffisant de la convergence |fn(t) - fm(t)| < et à un tel
but on s'applique le théorème dont de Lagrange 
tirant profit de la convergence ponctuelle dans t0 et de la convergence uniforme de la
succession silicium des dérivés {fndu '} elle établit la
convergence uniforme au f(t) de la succession {fn }.
b) Nous supposons que {fn(t)} il converge uniforme au monstre de f(t) que f
est derivabile, est eu : 
de ce que
qui est le rapport ils augmente tout derivabile qu'elle est
s'appliquer toujours obtenu à Lagrange et à la convergence uniforme
de la série des dérivés, les deux limites on peut dont échanger
que 
l'obtention la thèse.
7) théorème de l'échange de la limite avec l'intégrale :
On est la succession uniforme euef n des fonctions limitées par integrabili sur l'intervalle [ a,b ], convergente avec la limite f
dans combien est eu la succession fn converge uniforme à f. doit être seulement démontré l'integrabilità de f qui
fait en termes de subdivisions tirant profit de la convergence
uniforme de fn à f.
Série de fonctions
8) Critère de convergence ponctuelle de Cauchy :
L'état nécessaire et suffisant parce que la série de fonctions Sxn(t) converge ponctuellement dedans à est celui, fixé et > 0,
" t?À N(età,t) tel existe cela : |Xp(t) Xp 1(t)... xp q(t)| < et si n, m > N.
9) Critère de convergence uniforme :
L'état nécessaire et suffisant parce que la série de fonctions Sxn(t) converge uniforme dedans à est qui, fixé et > 0, existe N(et) tels que : |Xp(t) Xp 1(t)... xp q(t)| < et " t?Si n, m > N.
10) Critère de Weierstrass :
Donné à la succession des fonctions Xn et une séries convergentes des constantes positives Scn et définitivement il est eu |Xn(t)| £ cn
le la série de fonctions Sxn(t) converge uniforme dedans à.
On le démontre dans la vertu de l'inégalité triangulaire et du critère de la convergence de Cauchy de laquelle il dérive
|Xp(t) Xp 1(t)... xp q(t)| < |Xp(t)| |Xp 1(t)| ... |Xp q(t)| < cp cp 1 ... cp q < et
11) théorème du total de convergence :
Si {xn} le normato et accomplissent) dont la série des normes de S est une succession aux valeurs dans un espace de Banach (||Xn || c'est convergent converge également la série Sxn.
La démonstration trace déjà a gagné combien pour la convergence absolue de la série numérique, analogue tirant profit du Critère de la convergence ponctuelle de Cauchy et de l'inégalité triangulaire. Le théorème est dit du total de convergence dans combien une série pour laquelle la série des normes converge coûte totalement convergente .
12) théorème de la limite d'une série :
Si Sfn(t) est une série convergente
uniforme de fonctions avec F(t) additionnent et existe la limite
le la série lnde S converge et ha 
13) la somme d'une série convergente uniforme de fonctions continues est une fonction continue.
On doit démontrer la continuité de la somme de la série qui nous nous rappelons d'être égaux à la somme du n-esimo de repos et du n-esima partiel de somme, vu que l'incrément h a les deux égalités suivantes :
le membre 
de détournement de e au
membre est obtenu :
Là où pour 1ª on tire profit de la la somme de quart de cerclede fonctionscontinues qui S n (x) est et donc il continue tandis que pour 2ª et 3ª le quart de cercle le repos est tiré profit que la série est donc n-esimo convergent uniforme peut être rendue petit combien d'uode v.
14) théorème de l'intégrale d'une série :
Une succession f n des fonctions limitées par integrabili
est eue sur l'intervalle [ a,b ], si la série Sfn(t)
converge uniforme dedans (a,b) avec le de F(t)
de somme F est intégrable et est eue 
On se rappelle le que la somme d'une série de S
est égale au n-esima partiel de somme Sn(x) plus le n-esimo de repos Rn(x), intégrant et passant aux modules qu'il est eu : 
là où la convergence uniforme de la série a été tirée profit. Par conséquent le théorème est démontré.
15) théorème du dérivé d'une série :
On est la succession eue fn des fonctions de derivabili et
) la série des dérivés fnde S' il converge uniforme dedans (a,b) avec la somme de G(t)
b) la série de funzioni le Sfn converge au moins dans un point t0 ? (a,b)
le également la série fnde S converge l'uniforme dedans
(a,b) et il est eu 
S f n'est g(x) = étant convergent uniforme pour le théorème précédent peut être la limite intégrée a.termine
là où dans le dernier passage la convergence
à sa somme de la série de fonctions a été tirée profit. La
dérivation du (x) du s précédent d'expression et donc en (x) du s
de definitiva = le S f n 'est
g(x) obtenu =.
Série de puissances
16) si une série d'uniforme 
de puissances converge dans un point z0 ? C
le converge absolument dans chaque un tel point cela |z| < |z0|
Il est obtenu pour la comparaison avec la série
géométrique a en fait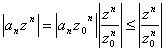 
où la convergence dans le
point z 0 pourle maggiorare avec 1 a été tirée
profit 
la limite. La dernière série est
géométrique et converge > |z| < |z0| dans qui enferment le rapport est plus petit
d'puis pour le théorème de la comparaison est 
également absolument convergent.
17) Critère de la racine afin de déterminer le faisceau de convergence :
Donné à la série le faisceau 
de convergence est
le
le è r = 1/l :
18) Critère du rapport afin de déterminer le faisceau de convergence :
Etant donné la série si le faisceau
de convergence existe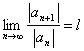 
limite le
le è r = 1/l :
19) propriété de la somme d'une série de puissances :
) la série elle converge uniforme en chaque cercle : |z| £ r 'avec r '< r
b) la somme de la série est une fonction continue dedans |z| < r
c) la série des dérivés est toujours une série de puissances qui a le même faisceau de la convergence
d) la somme de la série est derivabile dans le sens complexe avec le dérivé continu dedans |z| < r ; son dérivé est égal à la somme de la série des dérivés
a) démontre au moyen du théorème de Weierstrass en fait que la série converge absolument pour z = r 'étant intérieur il au faisceau de convergence et situé sur le vrai axe donc nous avons trouvé une série de constantes positives Sànr 'ces il converge et ce maggiora notre série de Sà nzn qui converge donc absolument.
b) En se rappelant que le f(z) de somme d'une série convergente uniforme de fonctions continues est continu et datez la convergence uniforme de Sà nzn dès que démontré et l'caractère arbitraire du point r ', le théorème s'avérera démontré.
on a c) 
que c'est
une série de puissances avec les coefficients bn = (n 1)an 1 ,
appliquant le critère de la racine 
est obtenu
et donc le faisceau de convergence est le même deà n .
d) E suffisant 'pour écrire fX et fy et pour vérifier qu'ils satisfont les relations de Cauchy - Riemann.
20) l'autre propriété de la somme d'une série de puissances :
) la somme de la série de puissances elle est de ¥ de la classeC dedans |z| < r
b) le k-esima dérivé de la somme de la série est égal à la somme de la série du k-esime de dérivés.
c) Entre les coefficients de la série
et les dérivés de sussiste du f(z) de somme la relation 
a) Segue du fait que la série des dérivés est toujours une série de puissances avec le même faisceau de la convergence.
b) E 'exactement le point d) du théorème 19)
c) est obtenu de la manière pratique dérivant la somme de la série
21) théorème d'Abel :
Si une série de puissances de Sà nzn converge dans un des points extrêmes de son intervalle de convergence
le l'intervalle de convergence inclut également ce point.
La convergence uniforme dont est eue si est démontré
le n-esimo de repos est plus petit et 
on peut 
écrire être de
laquelle rassemblant xn 
est
eu peut donc être tiré profit la convergence uniforme dont rend tout
le n-esimi de repos plus petit on obtient et / 2 rassemblant qui reste dans la parenthèse
le développement de la série géométrique pour laquelle la somme 
devient plus simple dont le n-esimo de repos est
plus petit et .
22) condition nécessaire pour le sviluppabilità en série de tailleur d'une fonction f :
C'est f ? ¥de C (- r, r) et un M constant,
indépendant existe de n et de x tel qu'est eu, définitivement 
le f est sviluppabile en
série de tailleur dedans (- r, r).
On remplace la condition dans l'obtention de n-esimo 
de repos 
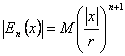qu'elle étire à 0
pour n qui s'étend au ¥.
