Théorèmes sur la série de Fourier
1) théorème d'Euler sur la détermination des coefficients de la série de Fourier :
Les coefficients de la série de Fourier sont déterminent à vous de l'intégrale 2 suivante ceux :
Du polynôme de l'oltiplicando 
de
Fourierm pour le cosmx (m = 0.1....,n) et
intégrer entre -p et p 
est eu. Se multiplier analogue pour le senmx (m = 0.1....,n) et
intégration entre -p et p il est eu 
.
Après avoir tiré profit de suivre remarquable d'intégrale :
;
;
2) identité de Pitagora Parseval :
Si le f(x) de fonction satisfait la condition de Dirichlet età n et à bn ils sont les coefficients de la série de de Fourier
On le démontre prenant trigonometrical polynôme, 
se multipliant il pour le f(x) et intégrant entre -p et p il est obtenu : 
après avoir tiré profit des intégrales 
, 
e 
.
3) théorème sur la convergence quadratique à la moyenne :
À changer de sn entre tout le polinomi trigonometrical du degré
n, l'écart type 
elle s'avère minimal si sn = sn où sn il est le n-esima partiel de somme de la série de
Fourier associée à f.
L'ajuster est remplacement
obtenu de e
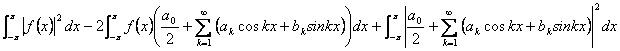
pour 1° la limite que l'identité de Parseval peut
être tirée profit tandis que pour 2° la limite le
polynôme est prise trigonometrical, il est multipliée pour 2f(x) et
intégrale entre -p et p. s'en avère la thèse.
4) inégalité de Bessel :
Il est gagné de la convergence quadratique à moyen
observant cela 
dans combien l'integranda de fonction
coûte positif, donc le résultat trouvé du fait le cas est valide
comme inégalité.
5) théorème sur la convergence ponctuelle :
Si f il est une fonction continue parfois et périodique avec la période 2p
le la série de Fourier du f
converge dans chaque point X dans lequel la condition de Dirichlet est
satisfaite et sa somme dans un tel point vaut la peine 
tandis que si x sont un point de continuité pour f puis la
série converge avec le f(x) de somme. Étant f(x-) = la valeur de la limite gauche et
f(x ) = la valeur de la limite habile.
6) théorème sur la convergence uniforme :
Si f il est une fonction continue et avec le dérivé continu à moins qu'au plus un n° ait fini que les points dans lesquels il est cependant respecté le n° de condition les 2 de séries de de Dirichlet de Fourier du f convergent absolument et l'uniforme dans ".
