Théorèmes sur la série numérique

Critères de convergence

1) Critère de Cauchy

La série est convergente > " et > 0 un tel $ N pour lequel chaque n > m, le ³ 0 de m qui est si le repos partiel est plus petit de et .

 

2) Corollario du Critère de Cauchy :

La condition nécessaire de sorte que la série converge est celle

Elle est obtenue à partir du Critère de Cauchy plaçant m = 0 et observant que " n > N doivent être |_{à n}| < et .

Critères de convergence pour la série aux limites non refusées à vous

 

3) Critère de la comparaison :

Si les séries etsont toutes deux aux limites non refusées à vous et si_n ³ 0de n de b le £ _{à n}le " >

) si la série est convergente, alors c'il est également la série

b) Si la série est divergente, alors c'il est également la série

c) Pour le critère de Cauchy, être convergentde b _n, a être alors " n à_n < b_n , suit qu'il est également donc pour le même critère de Cauchy que la série est convergente également.

 

4) Corollario du Critère de la comparaison

Si les séries etsont au positivi de limites etau ž du ~ b_{n de n} les 2 séries auront le même caractère.

Se rappelant que 2 séries sont asymptotiques si et peut donc être dit qui_{à n} est comporté entre 0.5b_n 1.5 eb_n et donc si comme exemple b_n diverge, il devra diverger également_{à n} .

 

 

5) Critère de la racine

Sic'est une série aux limites 0 non refusées à vous ž si le £ existe l < un 1 et un tel N que " n > N est eu

le ž la série est convergent

On le démontre en observant cela pour le ³ N de n qu'il doit êtreau £ l ⁿ_{de n} et donc la série converge dans combien coûte une série géométrique de raison l < 1.

 

 

6) Corollario du Critère de la racine

Sic'est une série aux limites non refusées à vous ž si la limite existež

) la série elle est convergente si l < 1

b) la série est divergente si l > 1

 

 

7) Critère de Raabe :

Le 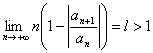ž de Se la sérieconverge absolument.

 

 

8) Critère du rapport :

S'il est une série à 0 positifs vous nomme et existe < l < 1 un tel un qui le ž la série est convergent

Elle est gagnée pour l'induction, si nous supposons pour chaque n est eus qui_{à 1} £ l_{à 0} ,₂ le £ l_{à 1} £ l (l_{à 0}) et donc par l'intermédiaire de donc sera doitle £ l ⁿ_{de n à 0} donc observant que la série de Slⁿ _{à 0} a le même un caractère de la série Slⁿ qui converge étant la série géométrique et le l<1, en suit que S à _n convergeégalement .

 

 

9) Corollario du Critère du rapport

Sic'est une série aux limites positives vous et existe la limite >

) la série il est convergent si l < 1

b) la série est divergente si l > 1

 

 

10) Critère intégral :

Si le f(x) il est une fonction positive, il continue et diminuer pour le ³ de x un tel N et ce f(n) =_{à n} et d'ailleurs existe fini

le ž converge.

Pour le monotonia il est doit_{n 1} = f(n) de £ de f(x) de £ du f(n 1) =_{à n} donc intégrant entre n et n 1 et tirer profit de cela sur les abscissas l'étape est celui-là des nombres normaux qui sont de 1 haau £ de £ _{de n 1 à n} et à ajouter l'intervallini

_{à 2} à₃ ...au £ de £ _{de m à 1} à₂ à₃ ..._{à m} . Il réalise une partie que qui si l'intégrale converge alors la somme du côté gauche sera en croissant et limitée advancedly et donc il admettra la limite.

 

 

11) Critère de condensation

Si {_{à n}} c'est une succession aux limites non refusées à vous et la diminuer alors converge > converge la série

 

Les critères de la convergence pour la série aux limites avec le randomico signent

 

12) si la série est ž convergent la série est convergente.

Si converge elle veut indiquer que pour le Critère de Cauchy un N existe : " n, m > N ha | _{à n} | |_{à n 1}| ... |_{à n m}| < et du repos pour l'inégalité triangulaire soyez également | _{à n à n 1} ..._{à n m}| < | _{à n} | |_{à n 1}| ... |_{à n m}| < et et donc le même Critère de Cauchy indique à nous qu'également la série converge.

 

Critères de convergence pour la série aux limites avec le signe alterné

 

13) Critère de Leibniz :

La série avec à_n > 0 "n est convergente à condition que :

) la succession_{à n} elle derising b)

On peut observer la limite génériquede la série est s_n =_{à 0} - _{à 1} à ₂ -....(-1) ⁿ à _n (où clairement les limites égales sont ajoutées et les limites inégales sont détournées) que l'égale a réduit ceux diminuent en fait s_{2n 2} = s_2n - (_{à 2n 1} -au £s _{2n de 2n}2) là où elle emploie le fait que {_{à n}} diminue donc la limite pénultième règne sur dernière. À l'effet contraire à la place réduits les inégaux ils sont l'infatti s _2n1 de croissants = s_{2n -1} (_{à 2n} -au ³s _{2n de 2n}1) _{- 1} .

Étant d'ailleurs s_{2n 1} = s_2n -_{à 2n 1} et à la limite générique à_n > 0 si de lui il déduit ce ³s ₁ de ³du ³ s _2n-1 du ³s _{2n 1}de s _2n.... où la diminution a été tirée profit dès que démontré donc la succession de l'égale a réduit ceux il diminue et limité inferiorly donc lui converge, suppose à S, le puits également la succession de réduite la inégale converge à S en fait reprenant le s_{2n 1} = s_2n -_{à 2n 1} et à sfruttando b) elle déduit que pour le ¥® ha s _2n1 de n = s_2n .

 

14) Critère d'Abel - Dirichlet :

Si {_{à n}} c'est une succession aux valeurs complexes dont a réduit le n-esime qu'ils sont tous qui limitent et {b_n} est une succession aux valeurs réelles qui étire le mente monotone à 0, le ž la série est convergent.

peut être le maggiorare où selon le membre il n'est pas autre ce la formule du sommazione analogue pour des pièces à l'intégration pour des pièces. Se rappelle que tout réduit n-esime _{à n} est dans le module plus petit de M et que {b_n } une succession décroissante qu'elle suit cela dont sommaire se développant ha = 2 b P.M. < 2 et M donc pour l'caractère arbitraire de et et le Critère de Cauchy est suivi qui la série est convergente.

 

Opérations sur la série

 

15) produit d'une série pour un nombre :

: = d'ailleurs la série a le même caractère de la série

 

 

16) somme de 2 séries :

: = et si les les deux les séries sont convergentes puis c'est également la somme de série.

 

 

17) produit (selon Cauchy) de 2 séries :

*: = essendo

 

 

18) théorème de considérer Mertens le produit (selon Cauchy) de 2 séries :

Siet elles sont 2 séries convergentes et l'un des 2 est également absolument convergent alors la série produiteest convergent avec la somme C=AB

Concernant la propriété associative et commutative la série

19) pour la série convergente ou divergent il vaut la peine la propriété associative qui est si une série de S est b créé_n dont chaque limite il est somme d'une partie de Sà_n , ž que les deux séries ont le même caractère.

 

20) si Sà_n est une série absolument puis chaque convergent son riordinamento est également absolument convergent et a la même somme.