Théorèmes sur l'intégration multiple

1)    à avec lui est le ž limité

À sa frontière est mesurable   > est mesurable et a la mesure 0

 

2)    si j'ai une fonction continue sur le contrat un ž mesurable de T

son diagramme est avec limité et mesurable et a la mesure nulle.

La fonction est continue sur compacte donc pour Heine - le chantre est-il également continu uniforme qu'il implique cela si je prends W 'et W '' ? T un tel che || W '- W '' || < d est alors che eu || f(w de f(w ') - '') || < et.

Une décomposition régulière (de diametro est effectué < d) d'un rectangle qu'il contient le dominion de T.

Pour Bolzano Weierstrass (si et le  "ⁿ il est une intégralité fermée et le ž limité Max(E) et Min(E) existent)

sur chacun de la volonté de T existent le maximum et le minimum de la fonction, et un intervalle de est créé "avec ³ tailles comportées entre le minimum et le maximum assumés de la fonction sur les espaces dehors. Par conséquent la mesure de la surface est indiquée de la somme des mesures de ces ³ intervalles de " qui est < et dans combien la fonction est continue sur compacte donc pour Heine - le chantre est-il également continu uniforme qu'il implique cela si je prends W 'et W '' ? T tels que || W '- W '' || < d est alors che eu || f(w de f(w ') - '') || < et.

3) le cilindroide est avec mesurable :

Assez pour démontrer qu'une sa frontière a la mesure tridimensionnelle nulle donc il est en fait vers le haut pour le f(x, y) pour le théorème précédent et est donc pour la base dans combien a la taille 0 comme pur pour la paroi latérale, tous les deux en fait peut être enfermé dans un plurirettangolo de "³ de la mesure infinitésimale.

 

4) si j'ai un contrat constant L de fonction sur mesurable de la base de T? "² et donc D est le cilindroide de la base de T, est eus :

On le suppose que la base est contenue dans le plurintervallo P₂ et contient le plurintervallo le Pqui est ₁ P₁ ? T ? P₂ a donc le m(P1) < m(T) < m(P2), du L repos est donc Lm(P constant1) < Lm(T) < Lm(P2) avec Lm(T) = m(D) est eu donc

|m(D) - Lm(t)| < L |m(P2) - m(P1)| le £ L et dans de combien pour le théorème du chantre de Heine si f il est continu sur un un puis f compact coûtent continu uniforme et donc si la distance entre les deux points du dominion est < ž de dla distance entre les images il sont plus petit et .

 

5) si j'ai une fonction continue sur le contrat par T mesurable? "² et donc D est le cilindroide de la base de T, est eus :

Pour le théorème du chantre de Heine être la fonction continue sur compacte est également continu uniforme donc choisissant une plus petite amplitude de d pour la décomposition régulière du dominion de T obtiendra une distance entre les images plus petites de et .

)    s_à,p = est comporté entre la somme de Cauchy qui emploie le minimum de la fonction sur chaque tuile de plancher de la décomposition régulière et la mesure de Cauchy qui utilise à la place le maximum.

b)    la mesure du m(D du cilindroide Si) est comportée entre la mesure du cilindroide qui emploie la valeur maximum du f sur chaque tuile de plancher et la mesure du cilindroide qui emploie la valeur minimale du f sur chaque tuile de plancher.

Elles donnent a) et b) le dato dont la différence entre le maximum et le minimum est sur chaque plus petite tuile de plancher et puis est che eu | s_à,p - l | < et en fait

 

6) formule de réduction pour de doubles intégrales :

Si f il est continu sur simple un dominion de T concernant le ž de l'axe X

Interprétation géométrique simple

 

7) formule de réduction pour des intégrales triples au moyen d'intégration pour des fils :

Si f il est continu sur simple un dominion de T concernant le ž xy de plan

Interprétation géométrique simple

 

8) formule de réduction pour des intégrales triples au moyen d'intégration pour des sections :

Si elle est doit < x < b et les sections de D avec un plan orthogonal à l'axe X soyez mesurable alors sont eus :

Choisissez l'interprétation géométrique

 

9) formule pour le changement de la variable :

Si He est compact mesurable ayant comme l'image et le r(u de T, v) c'est un biiezione dont le jacobiano n'est pas ž nul

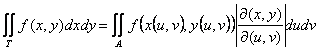
Interprétation géométrique simple

 

10) Pain De Guldino De Théorème :

Le volume du S plein qui est obtenu à partir d'une rotation complète autour à l'axe z de limité et mesurable contenus une intégralité de T dans le plan X = 0 est indiqué de la formule  étant la coordonnée du centroide.

Il est dépassement obtenu dans des coordonnées polaires et se rappeler la définition du baricentro 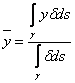.