Théorèmes sur les fonctions implicites
1) théorème des dynes :
C'est g : À® " , à ouvert "de 2 . Nous supposons cela :
) g par exempley ils sont continus dedans à.
b) dans le point X0 , y0 ? À un a le g(x0 , y0) = 0 et ¹0 de g y( x 0,y 0 ).
le un 0 existent autour Ude x et d'une seule fonction f : U® " , continue dans U, tel que y0 = le f(x0) et que le g(x, le f(x)) = 0 pour chaque x ? U.
Si d'ailleurs gX sont continu dedans au f qu'il est derivabile dans U et vaut-il la peine la
formule 
" x ? U.
La portée est celle-là à rapporter elle-même à
pouvoir appliquer le théorème des zéros sur un intervalle opportun (si une fonction continue définie sur un
intervalle [ a,b ] suppose à ses valeurs non nulles d'extrémité et
de signe opposé, puis f admet au moins un y zéro ? (a,b)) pour
l'endroit de l'intervalle s'applique le théorème de la permanence du
signe au gy que nous
supposerions g positify (x0 , y0) > 0 (si 
puis f(x) > 0 définitivement pour x ® X0 où la limite
indique définitivement que la propriété est valide pour chaque x
concernant au moins un autour de x0 avec le ¹ X 0de x .)
donc la fonction du g(x simple de y queles 0 ,y) augmentent étroitement et depuis le g(x0 , y0) = 0 nécessairement soyez
le g(x0 , y0 - b) < 0 g(x 0, y 0b) > 0 de e, d'ailleurs des relations analogues sont non seulement valeur dans x0 mais également dans une enveloppe
[ x0 - d , x0 d]. À ce point choisissant xconcerner le ce des enveloppes pour le théorème des zéros devra exister un y tels que le g(X , y) = 0 remplaçant et = b obtiennent que f il est continu dans vous l'enveloppe [ x0 - d , x0 d].
Afin de démontrer la formule le théorème du valor est
moyen utilisé (si f il est continu dans [ a,b ]
et derivabile dedans (à, b) le existe un tel point c qui 
) est donc le g(x eu, y) - le g(X,y) = 0 = gX(x)(x-de hx) gy(x,le)(y-de hy)
de ce qui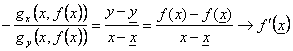 
est
obtenu.
2) théorème des dynes dans plus la variable de 2 ceux :
C'est g : À® " , à ouvert "de n 1 . Nous supposons cela :
) g par exempley ils sont continus dedans à.
b) dans le point X0 , y0 ? À x sont le g(eu0 , y0) = 0 et ¹0 de gy( x 0,y 0 ).
le un 0 existent autour U de x et d'une seule fonction f : U® " , continue dans U, tel que y0 = le f(X0) et que le g(X , le f(x)) = 0 par chaque x ? U.
Si d'ailleurs gx1 .., gxn est
continu dedans au f est
derivabile dans U et vaut-il la peine la formule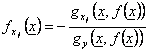 
" x ? U
Démonstration analogue à cela il est eu dans le cas tridimensionnel.
3) théorème des dynes pour des systèmes :
C'est g :® "m , à ouvert "de m n . Nous supposons cela :
) g il est derivabile dedans à.
b) dans le point (x0 , y0) ? À x sont le g(eu0 , y0) = 0 et ¹ 0du detD yg( x 0,y 0 ).
le existent un autour de V de x0 et un seul
une telle fonction y = f(x) que f est derivabile dans V
ED y0 =
le f(X0)
et que le g(X , f(x)) = 0 par chaque x ? V. D'ailleurs vaut la peine la formule 
.
Étant :
4) théorème de Lagrange :
Est-ce qu'ils le derivabili de f,g dans un X ouvert de " 2et (x 0,y 0)un point régulier sont sont pour et0 = {(x,y) ? "2 : g(x, y)=0}
le (x0 , y0) sont un 0 et un point > un $ critiques attachés un si vrai nombre l qui le f(x0de ` , y0) = l le g(x0de ` , y0)
le soit une question d'un point critique attaché (un point régulier pour lequel le dérivé de f dans la direction de tangente à la cravate) que le gradient de f lui est décommandé devra être normal à la tangente donc en date du gradient de repos de g doit se produire pour le porteur.
? De l'équation il découle que le gradient de f est normal à ensemble et0 dans le point (x0 , y0) et donc le point est limite critique.
5) méthode de multiplicateurs de Lagrange :
) il est nécessaire de caractériser les points singuliers de la cravate. Assez pour installer le Jacobiano de détermination et pour imposer qu'il est nul.
b) les fins libres du lagrangiana sont caractérisées.
c) la nature des points d'estremanti est obtenue à partir de l'étude des dérivés de la fonction implicite qui sont gagnés ou par le théorème des dynes ou le dérivé symbolique de la fonction composée.