Les théorèmes sur les équations les différencient ordinaires
Les équations les différencient du degré 1°
1) théorème des contractions de Banach - Caccioppoli :
Dans un espace métrique complet une contraction admet toujours un seul point fixe.
Existence :
pris un point X0 arbitraire nous construirons une succession qui converge à un ~ du pointX : Le ~de F(x) = successionde La de ~ de x est ricorsivamente défini comme xn 1 = F(xn). Tirer profit du fait que F est contraction il réussit pour établir cela
le d(xn 1 , le
d(x1 , x0 du £r n de xn)) avéré qu'il vient ont employé afin de démontrer que
la succession est fondamentale dans quelle quantité de Cauchy donné
qui le d(xn , £de x m) et . Il est eu en fait : 
quel rassemblement et on obtient le
remplacement de la somme de la série 
harmonique
qu'elle étire à 0 pour le ¥® de m étant 0 < r < 1,
donc la succession est de Cauchy et donc elle converge.
Supponiamo que la limitede l'argument converge alors au ~ de x tirant profit de la continuité du pu² de contraction de F pour devenir la limite de la fonction et donc pour démontrer qu'au ~de F(x) = ~de x .
Unité :
Nous supposons que 2 points fixes, la distance entre d'eux tirant profit de la définition de contraction, ne peuvent pas qui existent soient 0, donc les 2 points dans la vérité sont le même point.
2) état de Lipschitzianità pour f :
Si f et son respect dérivé partiel à y est continu dans le f de D est localement respect de lipschitziana à y, uniforme dans t.
On le démontre appliquant le théorème du milieu de
valor 
3) si la succession des fonctions continues fn converge uniforme sa limite f est une fonction continue.
On le démontre s'appliquant le théorème de l'échange
des limites à la fonction 
.
4) Lemma di Volterra :
Si j ? C1(le d) est solution du problème du j de Cauchy satisfait l'intégrale d'équation de Volterra 
" t ? Det viceversa.
le E 'clairement qui si j est solution du problème du de Cauchy il peut intégrer la première équation du problème entre t et t et remplacer la condition les commence j(t) = x .
? Il est dérivation obtenue dans combien j il coûte continu et il a dérivé continu dans la vertu de l'égalité avec 2° le membre.
5) théorème d'existence et d'unité locale :
C'est f : D® "n avec D ouvert "de n 1 , continue dans localement le lipschitziana D et dans D, respect à y et uniforme dans t
pour chaque point (t,x) ? D existe autourdu d de t tels qued = [t-d , t d] dans lesquels on est solution définie du problème de Cauchy. Une telle solution est seulement dans le sens que chaque autre solution coïncide avec j dans l'intervalle commun de la définition.
La démonstration est articulée dans les trois étapes suivantes :
) le correspondant est associé au
problème de l'équation de Cauchy de Volterra
b) un espace métrique complet est caractérisé
Un espace métrique complet est l'espace des fonctions continues sur compactes, donc " (t, x) ? D caractérise un G compact : = {(t,y) ? "n 1 : ||tt|| < a et ||yX||< b}, à son intérieur nous caractérisons l'espace métrique Y des fonctions continues avec le diagramme contenu dans G , Y : = { j ? C(Id) : ||j(t) -x||< b} c'est un espace métrique complet au pacte pour adopter le métrique du d(j de convergenceuniforme, y) = maximum || j(t) -y(t) ||
on démontre c) que le correspondant à l'équation de Volterra les travaille est une contraction et caractérise donc un seul point fixe qui est une seule solution.
À l'équation de Volterra que c'est les travaux
associés ils 
, caractérisant l'heure des
restrictions à d est en
position à la fabrication pour voir cette ébauche d'une contraction :
) nous voulons que ce soit F[y ] ?
de
Y 
étant M : = maximum || f(t, y(t) || nous devons imposer Md < b et donc d <
b/M.
b) Nous voulons que ce soit la
contraction qui est 
de quel tirer profit du
lipschitzianità local de f il est eu : 
là où la dernière inégalité est motivée du choix de
le métrique de la convergence uniforme. Par conséquent la
contraction à condition que le L est und < 1 > d < 1/L.
Choisissant d = minute (à, 1/L, b/M) le théorème est démontré.
6) conditionnent pour l'existence d'une solution habile de massimale :
C'est f : D® "n avec D ouvert "de n 1 , continue dans localement le lipschitziana D et dans D, respect à y et uniforme dans t
le est y :[t0 , b) ® " habile limité de solution de massimale de n un b = b
Pour démontrer.
7) Lemma di Gronwall :
Ils sont ? " un intervalle et un t ? Ils sont d'ailleurs u,v : ® Les " deux dedans I continu, fonctions non négatives et c et " .
Si 
" t ? I
" t?I.
supposant t > t est et se multiplier par 
dans combien
est eu fonction au premier membre diminue ayant le négatif dérivé
lui en fait : 
dans combien a le w(t) de £ de v(t) et le quindi W
'u(t)w(t) de £ de (t) = d'u(t)v(t) par conséquent 
donc 
.
8) théorème d'existence et d'unité totale :
C'est S : = (t1, t2) x "n Supponiamo que f il est défini dans S et ce dans S f est respect continu et localement de lipschitziana à y et uniforme dans t. Si d'ailleurs 2 un tel B positif existent et des constantes à celui ||f(t, y)|| £ À B||y|| " (t,y) ? S
" (t,x) ? S, j(t ;t,x) sont définis dans t1 , t2 .
Pour assez le théorème précédent pour démontrer que
le y(t) il est limité de sorte que l'intervalle à nous il soit
massimale, à un tel normando de but l'équation intégrale de
Volterra 
est eue :
Par conséquent y(t) elle est limitée et donc elle admet
la solution de massimale.
9) théorème d'existence et d'unité totale :
C'est f : (t1, t2) x "n ®" une fonction continue et totalement de lipschitziana dans Y avec L de constante
" (t,x) ? S, j(t ;t,x) sont définis dans t1 , t2 .
Pour démontrer.
10) le théorème de la dépendance des solutions des données les commence :
C'est f :D® "n continue et localement respect de lipschitziana à y, uniforme dans t. Supponiamo d'ailleurs que dedans autour du point (t0, x0) sont piqué dans lequel chaque solution qu'elle est définie dans un intervalle commun au tutte d'ailleurs si (t ,x) ®(t0 ,x0 ) j(t ;t,x)®j(t ; t0 , x0)
Les méthodes de résolution des équations les différencient de 1° l'ordre
11) la formule resolutive des équations les différencie linéaires :
Elles sont des équations dans la forme 
, l'intégrale générale est données de la formule :
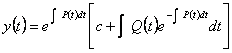
12) la formule resolutive des équations les différencie exactes :
Elles sont des équations dans la forme 
, l'intégrale générale est données de la formule :
étant F(t, y) une fonction les promeut
13) équations au separabili variable :
Elles sont des équations dans la forme 
, l'intégrale générale est données de la formule :
14) équations de Bernoulli :
Elles sont des équations dans la forme 
, elles résolvent le dividende pour yà et résoudre l'équation
d's'avérer qu'il différencie pour les tracer de 1° l'ordre.
15) équations homogènes ou de Manfredi :
Elles sont des équations dans la forme 
, elles résolvent le ponendo 
et
résoudre l'équation d's'avérer qu'il les différencie au separabili
variable.
16) comme des équations de résolution du type y = F(x, y ') :
Ce doit être y placé '= p donc pour dériver le respect à x, remplaçant donc p '= dp/dx une équation au separabili variable est obtenu résolvant quel le gain X et y selon p
17) équations d'Alembert - Lagrange :
L'ébauche des équations dans la forme f(y de y = de x ') 'g(y), est résolue plaçant y '= p donc pour dériver le respect à x, remplisseur donc à une équation linéaire en fonction du x se résolvant ce qui obtient une solution paramétrique de x et de y selon c.
Les équations les différencient de l'ordre n
18) Critère de base pour le trattazione :
Chaque équation les différencie de l'ordre n peut être menée de nouveau à un système linéaire des équations de n de 1° l'ordre donc afin de démontrer l'existence et l'unité de la solution, peut être faite recouru à combien déjà démontré par le equations les différencie de 1° la commande valide et également pour les systèmes linéaires au pacte pour changer le simbolismo.
19) état nécessaire et suffisant parce que les solutions de n de l'équation sont linéairement indépendant :
De détermination de la matrice de wronskiana doit être
0
¹ 0
20) théorème de Liouville :
Le wronskiano d'une équation les différencie de l'ordre
n satisfait la La 
Pour démontrer
21) théorème de Lagrange :
Ils sont y1 ..., les solutionsindépendantes de y n n de les homogènes, une solution de pas - homogène elle est fournie à partir de la formule
22) théorème de la superposition :
Si le b(t) = le b1(t) b2(t) et nous savent que une intégrale particulière de l'équation avec célèbre nomment b1(t) et un de l'équation avec célèbre nomment le de b2 (t) la somme du sarè de 2 intégrales que une intégrale de l'équation avec célèbre nomment le b(t)
Les systèmes des équations les différencient de 1° l'ordre
23) Critère de base pour le trattazione :
Les critères de l'existence et de l'unité locale et totale sont les mêmes ad.eccezione.della la notation.
24) état nécessaire et suffisant parce que les solutions de n de l'équation sont linéairement indépendant :
De détermination de la matrice de wronskiana ne doit pas
être nul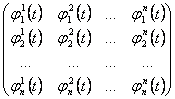 
25) théorème de Liouville :
Le wronskiano d'un système des solutions de l'équation 
satisfait l'équation les différencie 
où l'a(t) il est la trace de la matrice d'A(t).
26) Corollario du théorème de Liouville :
Le wronskiano d'une équation les différencie de l'ordre
n satisfait la La 
où l'a(t) il est la trace de la
matrice représentative
27) méthode de variation des constantes arbitraires (théorème de Lagrange) :
Afin d'obtenir la solution générale de la solution
particulière ricavabile 
de système non
homogène par la formule :
il est suffisant
ajouter à la solution générale du correspondant arrange le
homogène comme exemple 