" t?Étant un intervalle non dégénéré.

46) la solution générale d'une équation les différencie :

Elle est avec de toutes les solutions particulières de l'équation les différencie.

47) problème de Cauchy :

C'est un système constitué à partir d'une équation les différencie et ou plus de conditions il les commence qu'elles assignent incognito à la fonction que des données évaluent au moment t. A par le passé caractérisé l'intégrale générale peut être déterminé la solution particulière remplaçant les conditions les commence.

48) Fonction De Lipschitziana :

Le f(t d'application, y) est le lipschitziana à l'égard de D à y, uniforme dans t, si L constant existe une constante de préceptes d'un tel Lipschitz cela ||f(t, y)-f(t, z)|| £ L ||y-z|| pour chaque croisillon des points (t,y) et (t,z). dans D.

49) fonction localement Lipschitziana :

F(t, y) est localement le lipschitziana à l'égard de D à y, uniforme dans t, si chaque point de D possède autour en quel L constant existe une constante de préceptes d'un tel Lipschitz cela ||f(t, y)-f(t, z)|| £ L ||y-z|| pour chaque croisillon des points (t,y), (t,z) concernant autour. La différence concernant la précédente est donc seulement ce L peut dépendre dessus autour.

50) succession fondamentale ou de Cauchy :

Une succession est fondamentale si " et > 0 un tel N existe que 2 n'importe quels plus grands éléments n et m de N dans le dominio pris de la succession ayez elles-mêmes cela | _{à n} -_{à m} | < et

51) accomplissent Spazio métrique :

Un espace métrique est deto complet si chaque succession dans défini lui converge à un point du même espace.

52) contraction :

L'ove 0 d'application de Lipschitziana < L < 1 est un.

53) point fixe :

C'est un point qui vient transformé dedans si mêmes de l'application.

54) Spazio di Banach :

C'est un normato et un espace complet (chaque succession fondamentale est convergente).

55) intégrale générale d'une équation à l'élever de l'ordre de N :

est considéré où f : (à,b) X "ⁿ ®" est ž continu et totalement de lipschitziana

Est-ce que ladite intégrale générale du problème de la famille du correspondant un de Cauchy du y(t de solutions, c₁...,cn) est définie à changer de (t,c₁...,cn) ? X J₁ x.... x un telJ _n cela :

)    " fixé (c₁...,cn) ? J la fonction j(t) = y(t, c₁...,cn) est solution du problème de Cauchy

b)    " a fixé (t₀ , y₀ ..., y₀^(n-1) ) ? Le x "ⁿ existe (c₁...,cn) ? Seulement J tels que le y(t, c₁...,cn) satisfait les conditions les commence

56) l'intégrale générale d'un système linéaire des équations les différencie :

(t) est considéré y '= f(t, y(t)) où f : X "ⁿ ® "^{le n} est ž continu et totalement de lipschitziana

L'intégrale générale de y '(t) est dite = f(t, y(t)) un y(t de porteur, c) : (t,c) ? IxJ, J ? "ⁿ tels que :

à)    " a fixé c ? J la fonction j(t) = y(t, c) est solution

b)    " a fixé (t₀ , y₀) ? Le x "ⁿ existe c ? Un tel seulement J que j(t) = y(t, c) satisfait le y(t₀) = y₀ .

57) système linéaire :

L'ébauche d'une équation vectorial du type avec A(t) dicte la matrice des coefficients et limite célèbre de b(t) de ladite.

Quadriche

58) écrivent l'équation générique de l'ellissoide et pour décrire de changer :

l'ellissoide s'appelle parce que si nous le coupons le long de l'axe z = 0, x = 0, y = les sections 0 sont des ellipses.

changer est :

) si à selon le membre il y a alors l'ellissoide -1 est imaginaire

b) si la limite célèbre est 0 l'ellissoide est réduit à un point

59) écrivent l'équation générique de l'iperboloide à une strate et pour décrire de changer :

l'iperboloide à une strate s'appelle parce que si nous la coupons le long de l'axe y = 0 et x = 0 les sections sont des hyperboles tandis que si nous coupons le long des parallèles de plans à lui au plan xy nous obtenons des ellipses. Il n'a pas changer.

60) écrivent l'équation générique de l'iperboloide à deux stratums et pour décrire de changer :

l'iperboloide à deux stratums s'appelle parce que si nous le coupons le long de l'axe y = 0 et x = 0 les sections sont des hyperboles tandis que si nous coupons le long des parallèles de plans à lui au plan xy nous obtenons seulement des ellipses pour des valeurs avançées de |c|

il n'a pas changer.

61) écrivent l'équation générique du cône et pour décrire de changer :

C'est une équation homogène dans combien est évident tous les éléments du même degré veut dire qu'il peut être construit seulement en utilisant un paquet de directement. D'un point de vue mathématique elle coïncide avec la norme.

changer est.

) si le coefficient de z² est positif qu'alors le cône soit imaginaire.

62) écrivent les équations du paraboloidi et pour décrire des caractéristiques :

est un paraboloide elliptique, est évident que ses sections soient des ellipses, n'est pas qu'un gobelet convexe, parce que les valeurs de z plus petites de 0 vient ont décrit un paraboloide elliptique imaginaire.

est un paraboloide hyperbolique ou le Saddleback, est évident que ses longs parallèles de plans de sections au plan xy soient des hyperboles tandis que les parallèles de sezioni au yz de plan sont des paraboles concaves tandis que les parallèles de sections au zx de plan sont des paraboles convexes.

63) écrivent les équations des cylindres et pour décrire des caractéristiques :

est un cylindre elliptique

est un cylindre elliptique imaginaire

est un cylindre hyperbolique

est un cylindre parabolique

64) pour lequel des réductions de quadriche ils sont obtenus des plans ?

a) 2 l'autovalori et les correspondants annulent des limites linéaires

X² = ž de tn si les tn > 0 2 vrais plans sont des parallèles eus

si les tn = 0 2 vrais plans sont coïncider eu

si les tn < 0 2 plans complexes sont des parallèles eus

b) 1 autovalore 0 et d'autres 2 de discorde de signe, tn = 0

X² - le ž2 de y ² = 0 projette des incidents

c) 1 autovalore le 0 et d'autres 2 du signe de Concorde, tn = 0

X² incidentscomplexes de plans du ž 2 de y ² = 0 dont l'intersection est le vrai axe z.

Intégration multiple

65) intervalle de pluridimensionale :

_{Le 1} est le produttoria*_{les 2}*_{les 3}*... *_nl'être un intervalle limité des extrémitésau e b.

Sa mesure est

66) Plurintervallo :

Ébauche de l'union de P = étant elle-même Q_i un intervalle qui n'a pas d'autres points en commun avec d'autres intervalles.

La mesure du plurintervallo est égale à la somme des mesures des intervalles de Q qu'ils la constituent.

67) mesure intérieure limitée de avec à mle (a) :

L'ébauche de a contenu la fin avançée de la mesure du plurintervalli dedans à.

68) mesurent l'esterna limité de avec à m _et(a) :

Ébauche de la fin inférieure de la mesure du plurintervalli au lequel ils contiennent.

69) intégralité misurabile :

Une intégralité est ledit mesurable si la mesure intérieure et la mesure externe sont égales.

70) décomposition régulière :

Une famille des ensembles est ladite décomposition régulière de l'intégralité de T si :

)    chaque intégralité de Test limitée et mesurable

b)    l'union des ensembles le Tdonne en arrière l'intégralité de T

71) amplitude d'une décomposition régulière :

Ébauche du maximum des diamètres de T_i .

72) dominion :

C'est l'intégralité donnée de l'union de avec avec sa frontière.

73) Cilindroide :

Le plein caractérisé de I est-il des points X, y, z tels que x et y appartiennent au dominion de T? "² tandis que le z qu'il change entre 0 et f(x, y).

74) fonction intégrable en second lieu Cauchy :

Une fonction limitée indique intégrable selon Cauchy sur le contrat par T mesurable si étant : d  existe finito est l'amplitude de la décomposition régulière

À la décomposition régulière de T est on

p est avec des points m _ide I chacun de I qui appartient à un divers T_i .

s_à,p est la mesure de Cauchy égal à la somme

Les 0 limites sont finies si " et > 0 existent d ₀ > tels que pour chaque décomposition régulière à de l'amplitude d(a) < d₀ et pour chaque intégralité p des points est eu cela | s_à,p - l | < et .

75) dominion simple concernant l'axe X :

C'est un tel dominion au lequel < x < b tandis qu' à(x) < y < b(x)

76) dominion simple concernant l'axe y :

C'est un tel dominion ce c < y < d tandis qu' à(y) < x < b(y)

77) dominion simple concernant le plan xy :

C'est une intégralité constituée à partir des points (x, y, z) tels que x et y appartiennent au dominion tandis qu' à(x,y) < z < b(x,y)

Fonctions implicites

78) équation de la tangente droite au diagramme de la fonction implicite dans le point X₀ , y₀ :

79) avec de livello :

C'est l'intégralité dont est la projection obtenue sur le plan z = 0 l'intégralité obtenue intersectant le diagramme z = g(x, y) avec le plan z = c

80) point ou critico singulier :

Ébauche d'un point dans lequel le gradient du g(x ₀,y ₀)=0 de ` de fonction est ledit singulier im combien ne coûte pas applicable le théorème des dynes.

81) caractéristique de avec de livello :

Si avec du niveau il manque dans les points singuliers, dans chaque son point la tangente est orthogonale à la direction de l'augmentation maximum de g de ce point qui est le `g.

82) enveloppe d'une famille de courbe :

Ébauche d'une courbe de tangente, dans chaque son point non singulier, à une et une courbe simple de la famille.

Extrémités attachées

83) Jacobiano :

Il est de détermination d'être superficiel de matrice j ety d'"³ qui caractérise une courbe. Il représente la variation relative de taux du secteur, subordonnée au changement de la variable.

84) point régulier :

L'ébauche d'un point dans lequel le g(x, y) = 0 qui définit une fonction implicitement attachent l'affinche se produit, parce que le théorème des dynes doit être le g(x₀de ` , le ¹0de y ₀ ). Pour De Blasi à la place un point elle doit régler si le grade du Jacobiano est 2.

85) point critique ou stationnaire attaché :

Ébauche d'un point régulier pour la cravate dans laquelle le dérivé de la fonction objective dans la direction de tangente au vincolo. est décommandé pour De Blasi à la place que un point doit pour régler si le grade du Jacobiano est le £ 1.

86) Lagrangiana :

C'est le f(x d'equazione, y) - l le g(x, y)

Analyse vectorial

87) Parametrizzazione d'un sottoset d'"³ :

Ébauche d'une fonction continue r :® "³ dont l'image est le sottoset "de l'appui ³ également de la courbe et de coïncider avec la trajectoire.

88) Parametrizzazione simple :

Un parametrizzazione est simple si la fonction r est iniettiva.

89) courbe :

Parametrizzazione coïncide avec le croisillon (appui).

90) courbe plate :

c'est une courbe dont l'appui est contenu dans un plan.

91) direction d'un curva :

La direction est fonction du parametrizzazione, qui a comme le dominion " ce il est orienté et donc elle sera également de courber.

92) courbe régulière :

Un est-il eu le parametrizzazione derivabile de courbe et le r '(t) du ¹ 0 pour chaque t ? I.

93) l'équivalent courbe :

Deux courbes sont lesdits équivalents si elles peuvent être obtenues à partir de l'autre avec un changement de paramètre qui non sourd-muet la direction.

94) omotope de courbes :

Deux courbes g₁ et g₂ sont ledit omotope dedans et si une fonction continue existe j = j(t,l), (t,l) ? [ à, b]x[0, 1 ] tels que :

)    j(t,0) = r₁(t) ; j(t,1) = r₂(t) " t ?[ a,b ]

b)    j(à,l) = p_à ; j(b,l) = p(b) " t ?[ 0.1 ]

et finalement " l ?[ 0.1 ], la courbe g_l d'équation j = j(t,l) est contenu dedans et.

95) longueur d'une courbe :

Elle est obtenue s'appliquant le théorème de Pitagora à l'incrément infinitésimal afin de calculer alors le ds et ajoutant le ds.

96) abscisse curviligne :

C'est la distance couverte calculée le long de la trajectoire commençant d'un point les commence, il vaut la peine :

la dérivation d'un obtient (t) de ce s > 0 dans combien la norme coûte positive et donc le parametrizzazione au moyen d'abscisse curviligne est franchement équivalent.

97) intégrale curviligne des espèces 1ª :

À chaque élément infinitésimal de courbe la propriété est assignée un à la balance, l'intégrale curviligne des espèces 1ª ne fait pas autre que pour calculer la somme de ces contributions désirez ardemment toute la courbe, dans les formules :

dans le cas que f = la 1 intégrale donne en arrière à la longueur de la courbe, donc cette intégrale est indépendante de la direction de la même courbe.

98) des exemples de moi emploie de l'intégrale curviligne des espèces 1ª :

)    calcul de la masse du filo a

b)    calcul du barycentre du stesso de fil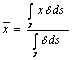

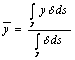
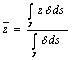
c)    calcul du moment de l'inertie d'un respect de fil à l'asse a

99) la forme différencie pour tracer elles ou 1-forma :

C'est la forme linéaire associée au champ vectorial F₁(x, y, z)i F₂(x, y, z)j F₃(x, y, z)k qu'il vaut la peine W = dzdy de dx F₂ F ₃de F ₁

le produit vectorial entre la force et le mouvement infinitésimal peut donc être pensé comme et représente donc le travail accompli de la force afin de déplacer son point d'application.

100) intégrale curviligne des espèces 2ª :

C'est le travail que le champ de F accomplit afin de déplacer son point d'application donne à à b.

Sa valeur est indépendante du parametrizzazione à condition que des dispositifs du parametrizzazioni équivalent qui est qu'ils maintiennent la direction.

101) la forme différencie pour les tracer chiusa :

l'écluse de W si putréfaction F = 0 ou est en d'autres termes dite si le champ est conservativo. Pour De Blasi à la place il est eu cela

W = dzdy de dx F₂ F ₃de F ₁ est écluse si X_y = Y_X, Y_z = Z_y , X_z = Z_X .

102) intégralités simplement reliées :

À et simplement chaque courbe est reliée si l'écluse dans contenu lui est frontière limitée de avec entier contenu dedans et c'est si chaque écluse de courbe peut être déformée jusque 2'au ridurla à un point restant à l'intérieur d'ensemble.

103) la forme différencie pour les tracer esatta :

W elle est dite exigent si une fonction existe des mises à niveau ils U qui est primitiva d'ossia de W F = le `U d'un point de vue pratique doit être commandé que W il est écluse qui est cette putréfaction F = 0 après quoi si le dominion est simplement relié, alors W il est exact tandis que si ce n'est pas puis W il est exact seulement localement.

104) facteurs d'intégration :

Le facteur d'intégration d'une forme est défini différencie pour les tracer que W pas exigent une fonction m un tel derivabile qui m W est exact, dans le plan est toujours possible pour caractériser un tel facteur l'intégration.

105) quant à calculent la fonction qu'il les améliore U :

Nous il doit avant évaluer que W il est exact après quoi la formule suivante est appliquée :

camm(a 106) de manière, b) :

Il est avec de toutes les distances qui combinent le point à avec le point b.

camm 107) de poligonale de manière_p(a,b) :

Il est avec de tout le poligonali qui combinent le point à avec le point b.

champ 108) vectorial de conservativo :

Un champ vectorial est ledit conservativo si une fonction existe des mises à niveau ils U dont le gradient est ` d'ossia de FU = F.

109) champ vectorial irrotationnel :

Un champ vectorial est ledit irrotazionale si putréfaction F = 0.

110) champ radial :

C'est un champ dont la valeur dépend en solo de la distance de l'origine, est un champ de conservativo, admet qui est des mises à niveau ils.

intégralité 111) de stellato :

Avec et c'est ledit stellato si des son ₀ points existentp tels que le segment directement de celui il le combine avec celui que l'autre point de l'intégralité entière est contenu dedans et.

Calcolo 112) des secteurs au moyen du théorème du vert de gauss :

la formule 113) de charge dans le plan :

C'est simplement une formulation vectorial de la formule du vert de gauss, a :

étant T le débiteur de tangente à la courbe délimitante D qui est obtenue dérivant le parametrizzazione.

formule 114) de la divergence dans le plan :

Ceci du théorème du gauss P de placement vert au lieu de Q et - Q au lieu de P obtenant à la première intégrale de membre de la surface d'une est également obtenue divergence et à 2° le membre le circuitazione du produit pour mesurer entre le porteur de F et le débiteur normal sortant. Dans les formules il est eu :

115) surface :

Une surface dans "³ est un croisillon (S,r) étant ³ S avec de " et r un son parametrizzazione.

116) point régulier d'une surface :

Un point p = r(u₀ , v₀) indique pour régler si la matrice a le rang 2 qui est est possible pour caractériser une représentation cartésienne de la même surface.

dominion 117) lentement de la Jordanie :

T est un dominion limité délimité à partir d'un bord par g simple orienté de circuit de T

118) bord positif d'un dominion de la Jordanie :

Est le bord positif ce qui il voit unanimement le croisillon rangé(t,n) constitué à partir du porteur de tangente et du porteur normal orienté au croisillon rangé du versori le I, j du plan. Une autre définition est que la surface doit toujours être couverte de porteur normal vers ensemble.

119) écluse extérieure :

La surface sans bord limité et dans " ³ estun .

120) surface régulière aux morceaux :

C'est une surface régulière pour laquelle ils existent un nombre fini des courbes régulières g ₁parfois ..., g_n contenu dans S qui le subdivise dans un nombre fini de lesdits visages réguliers superficiels.

121) coordonnent des lignes d'une surface :

u c'est la courbe qui est obtenue à partir du r(u de parametrizzazione, v) où v sont constants. Le porteur de tangente est r_u(u,v).

v c'est la courbe qui est obtenue à partir du r(ude parametrizzazione, v) où u il est constant. Le porteur de tangente est r_u(u,v).

Avec cette représentation il peut établir si la surface doit régler vérifier que c'est le ^r_v =0 de r _u.

équivalent 122) de Parametrizzazioni :

Sont le parametrizzazioni 2 attaché d'un changement de paramètre avec le jacobiano positif de détermination.

équation 123) du plan de tangente sur une surface dans un point :

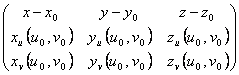= 0

124) porteur normal sur une surface :

C'est le porteur donné du produit vectorial r_u ^ r_v .

125) débiteur normal sur une surface cartésienne :

Il se gagne du dividendolode r _X ^r _y pour sa norme obtient :

126) vers du débiteur normal sortant dans le parametrizzazioni superficiel de cartésien :

Le débiteur normal externe est orienté sur la haute.

127) surface réglable :

Une surface est ledit réglable si régulier et lui est pris à l'n'importe quel circuit fermé et un point de P là-dessus, le porteur normal couvre de continuité le circuit fermé et le ripresenta dans le point de P avec la même directive. Les cas non réglables plus de drammati nous que superficiels sont la bande de Mobius et le wineskin de Klein.

128) secteur d'une surface :

129) intégrale de la surface d'un h(x de fonction, y, z) :

130) coordonné du barycentre d'une distribution de la masse superficielle :

Centroide 131) :

Ébauche du barycentre dans le cas particulier dans lequel la distribution de la masse il est constant.

132) moment de l'inertie d'une distribution de la masse superficielle :

133) 2_Forma :

C'est une forme de tipo W = le dz^dx Z de dy^dz Y de X dx^dy

134) écoulement d'un porteur par un S extérieur :

135) dominions simplement décomposables :

T ? "³ sont un dominion de la Jordanie simplement décomposable si T est relié et s'avère être disgiunta des syndicats d'un nombre fini de dominions simples de la Jordanie.

champ 136) de solenoidale :

Un champ vectorial F est ledit solenoidale si sa divergence est division de nulla F = 0.

137) ou intégralité reliée superficialally fortement reliée :

Une intégralité est dite superficialally s'est reliée si chaque écluse régulière parfois contenue de surface dans T délimite un dominion limité paraissant tout dans T.

formule 138) pour le calcul des mises à niveau elles porteur :

F = F₂j F₃k où e

139) quant à l'utilisation le théorème de la divergence pour le calcul des volumes :

y j z k sont nécessaire pour considérer le champ vectorial campo de F = de x pas F = j k qu'il donne en arrière toujours à un volume 0.

140) angle plein :

C'est dS par élément extérieur et nous combinons tous les points de la découpe du dS avec l'origine ou de venir d'une telle manière de former un cône. L'intersection entreune sphère centrale est l'heure d W ou et le faisceau r et le ž précédent de cône l'angle plein dW est caractérisé du rapport entre ce secteur et la place de la distance de l'origine être donc l'angle plein est .