Théorèmes d'analyse vectorial

1) premier critère de l'integrabilità du 1_forme :

Si W il est continu sur un D ouvert relié d'"³ alors

est-ce que W on a l'esatta > pris à, b concernant est-il à D qui avec g₁ , g₂ ? camm(a, b).

le ž pour la définition de l'intégrale de 1_forma a del rest si W qu' elle est exacte existe une fonction les améliore U, le primitiva de l'ossia de W F = `U = U_x U_y U_z sera eu donc et donc il regarde cela le della de valeur intégrale ne dépend pas dal couverte mais le point de dal commence seulement eux et le point de finale de dal.

? Sappiamo qui est indépendant de la manière, mais du point les commence seulement et de cette extrémité donc il est = U(b)-U(a), nous essayerons que le respect dérivé à x est égal à F₁ , de la manière analogue pour U_y et U_z et donc W est exact. Sont choisis donc de se déplacer de DX par le x(t) de parametrizzazione = le y(t) de xtD X = le z(t) de y = le z avec t?[ 0.1 ] pour le théorème de la moyenne pour les intégrales sera eu que la même valeur est assumé dans un point intermédiaire = , est eu après tout cela et donc passant à la limite pour DX®0 on l'a qu'u_X = F_1.

 

2) Corollario de 1° le critère de l'integrabilità du 1_forme :

Si W il est continu sur un D ouvert relié d'"³ alors

l'appui de W dans D est exact > pour chaque avoir le circuit est eu

le ž W est exact donc ne dépend pas de la manière mais ils donnent seulement à et b donc si nous prenons un circuit fermé et là-dessus nous caractérisons 2 points à et b que nous avons le che le long d'un côté du circuit est égal mais du signe opposé à et donc leur somme est nulle.

? Si tout le circuitazioni sont nul, trouve cela subdiviser un cycle dans des 2 circuits g₁ et g₂ , l'intégrale le long de g₁ est égale à l'intégrale le long de g₂ et donc pour 1° le critère de l'integrabilità du 1_forme, W elle est exacte.

 

 3) selon le critère de l'integrabilità du 1_forme :

Si W il est derivabile sur une intégralité alors simplement reliée

W que c'est esatta > W est écluse

ž Dimostro pour n = 2, analogue pour n > 2.

Si W il est exact puis pour la définition une fonction existe des mises à niveau ils un tel U qu'u_X = F₁ et U_y = ₂F dérivant 1ª le respect à y et à 2ª le respect à x obtient F_1y = F_2x qui est juste la condition de sorte que W il soit écluse.

?   la démonstration consiste essentiellement en calcul des mises à niveau elles au moyen de la formule usuelle. On l'observe cela :

)    dérivant U concernant z F ₃(x est obtenu, y, z)

b)    dérivant concernant y et en utilisant le che F ₂(x est obtenu, y, z)

c)    dérivant concernant x et en utilisant cela et ottiene F ₁de che(x, y, z)

après tous donc F = ` U est un cheeu qui est la définition di wexact.

 

4) théorème de gauss - verdissez dans le plan :

)    si D est un dominion de "² avec < x < b e j₁(x) < y < j₂(x) avec j₁(x), j₂(x) régulier parfois, est eu :

b) Si D est un dominion de "² avec c < y < d e y₁(x) < x < y₂(x) avec y₁(x), y₂(x) régulier parfois, est eu :

Je démontre à), de la manière analogue peux être démontré le b).

Pour 1° que le membre tirant profit de la formule de la réduction pour de doubles intégrales sur des dominions simples respectent à un axe est eu :

Pour 2° le membre à la place le circuitazione est estimé en observant cela dans les dispositifs rectilignes dx=0 et donc aussi l'intégrale :

et donc les 2 intégrales sont égales moins du signe.

 

5) Corollario du théorème du vert de gauss dans le plan :

Si D est un dominion limité dans "² dont la frontière est une courbe de la Jordanie régulière parfois et cela elle est simple respectent les aux deux les as. Si f = ž de pi Qj vaut la peine la formule .

Un est obtenu à partir du théorème de la formule de détournement verte de gauss de l'autre membre au membre.

 

6) démonstration au moyen de vert de gauss de 1° le critère de l'integrabilità du 1_forme :

Ils sont g₁ et g₂ deux délimitant courbe une intégralité de D. si F(x, y) est un champ vectorial derivabile et irrotationnel (putréfaction F = 0) qui est P_X = Q_y dans D. ž .

Pour l'égalité du théorème du vert de gauss on l'a que = 0 étant Q_X = P_y du repos que la frontière de l'intégralité est constituée à partir de g₁ a couvert dans le sens dans le sens contraire des aiguilles d'une montre et g₂ a couvert dans le sens d'heure dans combien intérieur à g_{la 1} égalité de pertanto est vérifié.

 

7) le théorème de charge dans l'espace :

Si S est une surface régulière contenue aux morceaux dans un ouvert de ? "³ et F = Qj dévot Rk un ž vectorial derivabile de champ

C'est r(u, v) = x(u, y(u de v)i, z(u de v)j, parametrizzazione du v)k un du ž extérieur

Partant à la place du circuitazione est écrit pendant que le correspondant 1_forma considère donc pour le semplicità le solo, étant,l'écrivant pour étendu et nous appliquant au théorème du vert de gauss le remplisseur à une double intégrale semplificabile pour des moyens du théorème sur les dérivés mélangés de Schwarz étant lui-même heure par fonction composée, ses dérivés est et remplaçant, développant les produits et devenant plus simple est obtenu dans lesquels les limites entre la parenthèse sont jacobiani de deteminanti.

Le fonctionnement de la même manière également pour les autres des membres et ajouter la thèse est obtenu.

 

8)    théorème d'Ostrogradsky :

C'est D ? "³ un dominion limité dont la frontière est une une extérieure d'écluse, régulière et réglable :

Si D est respect simple à un des as il vaut la peine un de suivre :

Si le dominion est simple concernant tous et les trois as ajoutant alors le membre au membre sont eus :

Je démontre seulement troisièmement dans le cas d'un dominion simple concernant l'axe z :

Partant de l'intégrale triple, il peut être décomposé pour par l'intermédiaire de du semplicità du dominion, a lui-même :

Laissant à heure à la place de 2° le membre il sera arrivé au même résultat, on doit en fait tenir le compte que la frontière du dominion est constitué à partir d'un chapeau avançé, un chapeau inférieur et une paroi latérale parallèle à l'axe z sur lequel l'intégrale est nulle dans combien coûte un écoulement et le porteur normal sur la surface est orthogonale au porteur k.

La mise en oeuvre d'un changement de parametrizzazione et observer que la surface avançée est orientée franchement tandis que ce subordonné est orienté négativement d'elle suit que le même résultat obtenu s'avère partir de l'intégrale triple.

étant le jacobiani dans l'issue égale à 1.

 

 

9)    théorème de la divergence dans l'espace :

C'est D ? "³ un dominion limité dont la frontière est une écluse extérieure, le régulier et réglable d'ailleurs sont D par dominion simple concernant tous et les 3 as cartésiens, F = Qj dévot Rk est alors un ž vectorial de la classe C¹ de champ

Il est ajouter obtenu s'avère à vous a contenu dans le théorème d'Ostrogradsky.

 

10) si F = à Bj Ck est de la classe C²(t), T ? "ž ³ ouvert superficialally relié

F est un rotor > un F est solenoidale

le ž   F est un rotor qui est existe des mises à niveau ils un tel porteur de U que le rotU = de F la division donc putréfaction de F = de division U = 0 et donc F est solenoidale dans combien a la divergence nulle.

? Afin de nous démontrer que F est un rotor de lui essayons des mises à niveau elles porteur U = zk du yj XI, il devons il sommes tels que

le rotU = l'ossia de F 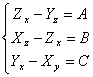afin de devenir plus simples est des mises à niveau essayées elles porteur avec le troisième membre de nulle qui est U = XI le yj 0k donc que le système simplifié est 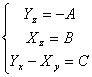heure de nécessité à élaborer les 2 premiers et les remplacer dans le 3ª, les intégrant concernant z ont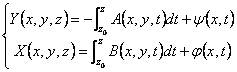

pour le semplicità nous supposerons j(x,t) = 0. Dérivation 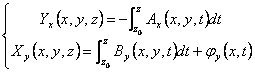quel remplaçant elle est eue : et tirant profit de l'hypothèse du nulla donc C de divergence_z = -_{à x} - B_y a qui est et respect d'intégration à y il est eu : supposer à(x) = 0 et le remplacement dans les premières équations obtient la thèse.

 

 

11) théorème des mises à niveau elles porteur :

Si à lui est un ouvert simplement relié d'"³ et V sont un solenoidale derivabile de champ vectorial (division F = 0)

le ž   Esiste un champ vectorial une telle putréfaction de che de F F = V dedans à chaque Inoltre d'autres mises à niveau ils porteur est donné de la forme

Diplômé jde F où j ? C²(a) est un à s'élever.

Le F est écrit la putréfaction considérant nulle le membre le long de l'axe i, de la putréfaction de vettoriale d'équation F = V obtient trois équations de scalari, satisfaites en termes d'intégrales, elles doivent à ce point seulement caractériser les constantes qui jaillissent de l'intégration, ce qui ce sont remplacement possible dans et tirer profit du fait cela

la division F = 0 est des mises à niveau obtenues elles porteur F = F₂j F₃k où e

 

 

12) caractéristique des champs de solenoidali :

Les superficiels sont eus 2 qu'elles sont frontière d'un limité s'ouvrent, et sont D le dominion constitué à partir de l'interstice entre deux les superficiels, bon si dans ce dominion la divergence d'un champ vectorial F est 0 ž que le traverser un de le superficiel est égal au traverser l'autre.

 

13) théorème de gauss :

Une surface est écluse de S et est r la position de porteur qui indique la distance de l'n'importe quel point (x, y, z) d'origine 0. Vaut la peine 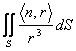alors :

)    0 si l'origine est externe à l'écluse extérieure

b)    4p si l'origine est intérieure à l'écluse extérieure.

) la divergence de r/r³ un résultat est le deuxième classique nul, donc cet écoulement est nul également.

b)    la divergence est nulle également cette fois mais au pacte d'éliminer un sferetta du faisceau infinitésimal dont la surface va parimenti considéré pour le calcul de l'écoulement.

 

14) interprétation géométrique du théorème du gauss :

C'est dS par élément extérieur et nous combinons tous les points de la découpe du dS avec l'origine ou de venir d'une telle manière de former un cône. L'intersection entreune sphère centrale est l'heure d W ou et le faisceau r et le ž précédent de cône l'angle plein dW est caractérisé du rapport entre ce secteur et la place de la distance de l'origine être donc l'angle plein est .

En bref si la source est extérieure à l'écluse extérieure puis à chaque contribution positive quand l'écoulement entre dans la surface une contribution correspondra négatif quand l'écoulement en sort. Si à la place la source il est intérieure puis les 2 contributions sont ajoutées et le total plein d'angle est égal au secteur de la sphère unitaire qui est 4p.

 

15) signifié de la divergence :

La divergence d'un champ vectorial F dans le point de P est donnée 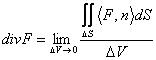de l'être DV le volume joint de la surface dS, un tel volume à la limite est réduite au point de P.

Elle est obtenue pour partir du théorème de la divergence étant appliquée le théorème de la moyenne pour des intégrales et localisant donc dans 1° le membre la divergence, faisant alors la limite obtient la thèse dont a signifié le physicien que c'est l'écoulement clairement par la surface dS qui a du le champ de F, si un tel écoulement est positif, veut dire qu'il y a une source intérieure tandis que si l'écoulement est négatif veut dire que la source est extérieure. Si la divergence est 0 il signifie que dans la région pas les sources sont des piscines de et donc le champ est solenoidale.

 

16) signifié du rotor :

Un champ derivabile F est F : T® "³ et est S_r par avoir le centre de disque dans P, faisceau r et directive caractérisée du débiteur normal externe n. 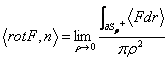ž .

On obtient pour partir du théorème de charge l'application le théorème de la moyenne pour des intégrales et localisant donc dans 1° le membre le produit du rotor pour le débiteur normal sur la surface, faisant alors la limite obtient la thèse dont a signifié le physicien que c'est que le rotor caractérise la direction dans laquelle la densité superficielle du circuitazione de F dans P est maximum.