1) décrivent l'espace vectorial Rⁿ :

C'est le produit cartésien de l'intégralité de R de n le vrai pour si les mêmes fois de n qui est Rⁿ = R * R * R *.... * R.

En particulier un porteur vient représenté avec ses coordonnées rapportées concernant l'origine, une telle origine peut changer au deuxième de la valeur de n.

Pour n = 2 nous trouvons dans R² qui est le plan cartésien ou.

Pour n = 3 nous nous trouvons dans R³ qui est dans l'espace ou.

Pour n = 4 nous ne réussissons pas pour imaginer que la sorte de l'espace représente, de quelque manière qu'ou.

 

 

2) vrai Spazio vectorial :

Un espace vectorial est vrai défini si dans lui les opérations suivantes sont définies :

1) est dans le présent lui l'élément 0 , ébauche d'avoir le porteur toutes les coordonnées avec le coefficient 0.

2) l'addition du ž de vettori est effectuée graphiquement avec la règle du parallelogramma et pratiquement

= = ébauche d'un porteur du plan sortant de l'origine et d'aboutir au point de l'abscisse coordonnée = 3, commandé = 8.

 

Pour la somme d'ailleurs la propriété 4 ou les axiomes sont définis après :

a) ASSOCIÉS Và VOUS au ž " x, y, z ? V x y z = (x y) z = x (y z)

b) COMMUTA VOUSV au ž " x , y ? V x y = y X

c) ž NUL " x ? V x 0 = x

d) ž " x du PORTEUR OPPOSTO ? V $ X¹ ? V : X x¹ = 0

3) la multiplication entre les porteurs est une opération que dans Rⁿ n'a pas le sens, au lieu de cela est employée la multiplication d'un porteur pour s'élever, et elle exécute le moltipicando toutes les coordonnées du porteur pour que celui-là monte l.

5= =

 

Pour la multiplication d'ailleurs est défini après avoir suivi la propriété 4 ou les axiomes :

a) ASSOCIÉS Và VOUS au ž " x ? V, "l , m ? R X (lm) = (xl)m = (xm)l

b) ž DISTRIBUTIF " x de la SOMME SCALARI ? V, "l , m ? R X (l m) = xl xm

c) ž DISTRIBUTIF " x , y de la SOMME VETTORI ? V, "l ? R (x y)l = xl yl

d) UNITA ' ž " x ? V x * 1 = x

R[x ] = polynôme avec des coefficients complexes de variable le x est un R typique de l'espaceⁿ avec l'égale de n au degré du polynôme.

 

Tout combien nous avons dit pour Rⁿ est applicable également à Cⁿ avec la seule différence qui dans les définitions devra être remplacée l , m ? R^{de n} avec l , m ? Cⁿ étant C, avec de n les complexes, donc les opérations de produit et de somme disparaîtra en second lieu exécuté affirmé combien pour n les complexes.

C[x ] = polynôme avec des coefficients complexes de variable le x est l'un espace typique Cⁿ avec n égal au degré du polynôme mêmes.

Nous avons démontré que la propriété des axiomes sont vérifiées dans Rⁿ .

 

2) produit à s'élever dans ⁿ:

Doit la disposition 2 porteurs, de multiplier un pour l'autre n'a pas un certain sens, mais elle a à la place le sens d'exécuter le produit à l'élever des 2 porteurs, ceci est obtenue qui exécute la somme des produits vous commande des éléments simples des porteurs

v : = , W : = < v,w > = (-1*4) (1 * 3) (4 * 6) (3*1) = 26

En tant que célèbre le produit pour s'escalader représente un n° dont a signifié qu'on le déduit de la conception suivante :

^{b = p/2} 

C'est le produit à s'élever n'est pas que le n° pour lequel nous devons multiplier l'affinche du porteur W il coûte le long de combien la projection orthogonale de v sur son directeur.

Le produit à s'élever pour être tel doit avoir la propriété suivante :

1) Commutativa < x, y > = < y, x >

2) Distributiva < x, y z > = < x, y > < x, z >

3) Omogeneità l * < x, y > = < lX, y > = < x, ly >

4) Positività < x, x > > = 0

En particulier donc le produit à s'élever est en position au dirci si 2 porteurs sont orthogonaux, en fait dans tels cas que la projection sera nulle et donc également le produit s'élèvera.

 

3) norme :

La norme intimement est attachée au concept du produit vectorial, le représente également un n° pour monter que ce temps n'est pas legs à la projection d'un porteur sur un autre bens¬ à la longueur d'un porteur, le deuxième dit combien coûte facile de le soumettre au théorème de Pitagora du duquel il dessine la nombreuse propriété mais quelle conséquence seulement dans le cas est dirigée dans lequel elle vient a considéré un angle de p / 2 entre 2 porteurs.

La norme vient toujours fait rapport à un seul porteur.

|| X || = =

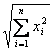
c'est lui est équivalent à la racine du produit à l'élever du porteur pour si même et donc à la racine de la somme des places des éléments simples du porteur. La norme doit posséder les 3 descendants suivants de propriété immédiatement également qu'ils donne le produit à l'élever :

1) || X || > = 0

2) || l * x|| = | l| * || X ||

3) || X y || < = || X || || y || ; c'est directement le théorème du pitagora dans lequel la hypoténuse la triangle est non sûre que plus petit des autres 2 côtés autrement seraient fermés.

La troisième propriété est fille de l'inégalité de Cauchy - Schwarz qui indique :

| < x, y > | < = || X || * || y ||

 

 

4) Sottospazi Vectorial :

Choisi un sottoset de l'espace vectorial V , il peut être ou moin'un sottospazio vectorial, il il est dans le cas sont vérifiés toujours la propriété qui distinguent un espace vectorial qui est :

1) présence du 0.

2) somme entre les porteurs.

3) multiplication d'un porteur pour qu'un s'élève.

D'une façon généralisée mais d'un système court existe également afin de vérifier si un sottoset d'un espace vectorial il est un sottospazio vectorial, la nécessité après lequel est soit satisfait :

W ? V un sottospazio Se est-il vectorial " W₁ , W₂ ? W e " l , m ? R

également lW₁ mW₂ ? W

Ce système est complètement équivalent au premier dans combien à riconducibile il, en fait :

l'affaire 1) peut être placée l = m = 0

l'affaire 2) peut être placée l = m = 0

l'affaire 3) peut être W placé₁ o m = 0

En particulier :

le sottoset est le plus petit sottoset et appartient à chaque espace vectorial.

le sottoset V est le plus grand sottoset et appartient à chaque espace vectorial.

 

5) les constructions produisent d'eux du sottospazi :

Nous commençons à définir une combinaison linéaire comme porteur constitué à partir du produit des porteurs de k concernant l'espace vectorial de V avec i coefficienti ₁..., _k. Il est présenté donc dans la forme :

3v₁ 5v₂ 2v₃ ... 14v_n

Pour effectuer l'envergure d'un porteur v ? Le moyen vectorial de l'espace V de produire d'un sottospazio de le même, ceci se produit comme exemple un semplicemente pensant à côté des multiples d'un même porteur, mais plus d'une façon généralisée, ayant 2 porteurs l'envergure représente toutes les combinaisons linéaires possibles de les mêmes qui est la somme des produits des porteurs simples pour le coefficient respectif _{à x} chacun de I qui peut assumer n'importe quelle valeur concernant ".

Noter que l'affinchè l'envergure il est un sottospazio doit être vérifié les conditions du critère court ou le long critère de l'endroit du sottospazi, celui est :

Critère de lungo : 1) présence du 0.

2) somme entre les porteurs.

3) multiplication d'un porteur pour qu'un s'élève.

Critère court : W ? V un sottospavio Se est-il vectorial " W₁ , W₂ ? W e " l , m ? R

également lW₁ mW₂ ? W

Un exemple typique de l'espace vectorial est qu'on a décrit d'un système homogène, cela a toutes les limites célèbres = 0 ;

l'envergure d'un espace vectorial semblable il est gagné trouvant simplement les solutions du système par la réduction de gauss. Ces solutions peuvent donc être écrites comme la combinaison linéaire plus de porteurs. Exemple :

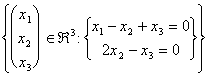
Il demande à nous déterminer le sottospazio vectorial dans "³ constitués à partir de toutes les solutions possibles pour ce système ce que le bidon généralement sont écrits comme l'envergure d'un n° des porteurs variables entre 1 et n.

Comme dire précédemment afin de résoudre le système s'applique le gauss à la matrice d'associé :

l'ébauche d'un système déjà à avoir la balance avec une libèrent incognito la solution dans le porteur :

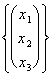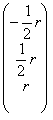= ce dernier porteur peut également écrire r *

Cette dernière forme indique à nous que ce sottospazio de "³ peut être décrit comme l'envergure

c'est lui est un espace vectorial constitué à partir de tous les multiples de ce porteur qui sont obtenus à changer de r qui est du libre incognito qui est associé à x₃.

Le cas existe naturellement également dans ce que l'envergure il est constituée à partir de plus qu'un porteur et ceci se produit toujours quand la solution du système des équations visionne plus d'un incognito librement. En particulier le n° des porteurs de l'envergure qu'il est égal au n° incognito en fait de l'ognuna libre ira multiplier un porteur et du fait le porteur nous elles devra être les coefficients de ce incognito les associés libres vous à respectif le x tandis que pour les autres x les coefficients dans le porteur dans l'issue devra être chacun des 0.

Comme exemple il est censé trouver dans un système les solutions suivantes :

= = r s t

et donc :

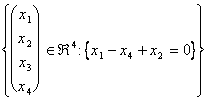= envergure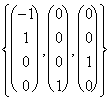

C'est de noter que l'envergure est un générateur des espaces vectorial qui pourront être déterminent les proportions également supérieures, celle sont sont possibles pour s'ajouter à l'envergure dès qu'écrit également un autre porteur qui si pas est également le ricorsivo mais qui il d'une façon minimum ne change pas la définition de l'envergure qui a été déclarée.

 

6) linéairement porteurs indépendants, employé, concept de base et dimension :

En partant de l'exemple précédent et de la limitation que nous avons dits est implicite dans l'envergure, demandez-vous combien de porteurs à nous sont efficacement nécessaires afin de décrire un espace vectorial ?

La réponse est semblable au concept du divisibilità de n^{le 1} qui est a la nécessité dont de n d'abord nous analogues savons pour être indivisibles et produire de tous les autres numeri., nous a le besoin d'une base qui est des porteurs de n par lesquels pour construire à tous les autres porteurs du plan comme lineare de combinaison.

La base d'un espace vectorial commandé est définie donc avec des porteurs v_1...,v_t de V tels que :

1) envergure { v_1...,v_t } = V.

C'est l'envergure doit être en position à décrire tout le V

2) les porteurs v_1...,v_t sont entre le indépendant eux.

C'est nous qu'ils ne doivent pas être des relations entre 2 porteurs ou plus de l'envergure, comme exemple ne peut pas être un multiple de l'autre. En particulier dans la combinaison linéaire ils devront être le 0 tous les coefficients l , donc en fait nous sommes seulement sûrs qu'il y a une certaine relation entre les porteurs pris en compte.

Si aussi un des coefficients que l est seulement divers de 0 alors dans l'envergure est des porteurs superflus donc les porteurs n'est pas tout le linéairement indépendant et donc ils sont linéairement défini employé.

D'ailleurs la dimension d'un espace vectorial V est définie, dim(V) le n° des porteurs desquels la base est constituée.

Elle sera juste ceci dès que déclaré la caractéristique qui différencie les espaces vectorial concernant la base, en fait chaque espace vectorial a une base mais les 2 cas suivants peuvent être présentés :

1) Spazio vectorial beaucoup de grand un ž est le cas du polinomi "[ X ] = un txcx ².... ⁿ du bx¹ , dedans ils que la base existe mais elle a des dimensions infinies.

2) Spazio avec le ž de finita de dimension a infiniment un n° des bases, celui est tous les porteurs qui sont entre de indépendant elles, toutefois nous savons que la dimension de ces bases doit être égale pour tous.

Dimostrazione : est procédée pour le dimostrando d'absurdité que 2 bases avec la diverse dimension appartiennent au même espace vectorial, afin de le faire écrit les porteurs de la grande base comme la combinaison pour tracer des porteurs de la petite base.

À ce point afin de démontrer que les porteurs créés ne sont pas donc indépendants, je rassemble tous les coefficients dans une matrice et je deviens compte que le n° des équations est subordonné du n° d'incognito, donc serai des libres incognito qui correspondent assurément à une dépendance des porteurs dans l'issue entre d'eux, donc n'étais pas une question d'un divers bas mais de la même base.

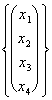
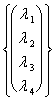
Nous avons déjà vu comme gagner une envergure, nous voyons l'heure comme l'évaluation à nous que les porteurs de l'envergure sont linéairement indépendant. Comme exemple nous ont les porteurs suivants ? "⁴ :

, ,

qu'ils peuvent être écrits comme une combinaison linéaire :

l₁ l₂ l₃ l₄

qu'il donne la vie à la matrice d'associé :

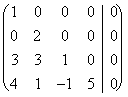ce qui donne comme la solution =

Par conséquent les porteurs sont linéairement indépendant et pourraient donner l'endroit à une base de l'espace considéré.

si à la place la matrice il avait été suivante :

cela réduit devient

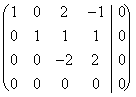
c'est une matrice avec une équation qui est décommandée et qui donc elle donne à la vie à une incognito librement qui rend les porteurs de l'employé linéairement décrit d'envergure que c'est nécessaire mais démontrer toujours l'obtenir un cas dans lequel la combinaison linéaire il est 0 mais ils ne sont pas le 0 tous les coefficients l. Par conséquent :

= r et donc placement r = 1 : - 1 - 2 1 1 =

Nous avons démontré qu'une solution où tout le l 0 ne sont pas = satisfait le système également donc que ces porteurs est linéairement employé et ils ne représentent pas donc une base.

Vous notez géométrique signifié après :

Linéairement indépendant

* 2 porteurs dans "² sont indépendants s'ils ont de diverses directions

* 3 porteurs dans "³ sont indépendants s'ils ont distingué des directions

Linéairement employé

* 2 porteurs dans "² sont employé s'ils ont la même direction

* 3 porteurs dans "³ sont employé s'ils ont la même direction ou ils sont trouvés lentement sur la même.

* 4 porteurs dans "³ ne peuvent pas cela être linéairement employé

 

7) affirmations sur lesquelles la recherche d'une est base basée :

) E 'une intégralité Massimale qui est constituée à partir des porteurs entre de indépendant elles qui vont bien à l'employé si le gliene elle vient a additionné 1.

 

b) une base est un cas typique de avec massimale

Faible : nous prenons une base de B de V, nous ajoutons un porteur à lui de V et nous notons que les porteurs donc obtenus sont linéairement employé dans combien si nous écrivons à ce porteur v en tant que combinaison linéaire des autres et alors de 1° le membre nous le portent au 2° que nous devenons compte qu'il a le coefficient 1 tandis que les autres porteurs ont tout le coefficient 0.

c) Si V = envergure (a) et B ? À lui est avec le massimale puis est également V = envergure (b)

on le démontre en observant que si est un porteur v qui n'appartient pas à B, alors pourra-t-il lui-même être écrit qui est comme la combinaison linéaire des porteurs à B et à? Span(B) et donc sera également V = envergure(b).

d) Chaque espace vectorial qui contient un système fini des générateurs admet une base

Faible : le ž est V = Span(A) :

d1) V = { 0 } alors V n'ont pas la base

d2) nous confrontons v₁ avec tous les autres porteurs, s'ils sont toutes les comparaisons des employés alors que la base est altrimentide v ₁ nous prenons les comparaisons qu'ils ont données comme le résultat des porteurs indépendants, nous comme exemple ont 2 porteurs v₁ et v₃ qui sont indépendants et des candidats à être une base, alors nous les confrontent avec tous les autres porteurs avec quel v₁ avait été le indépendant indiqué, et si également ces 3 porteurs sont indépendants puis nous continuons à confronter avec les autres porteurs cela il confronte à vous avec v₁ a eu le indépendant de résultats de données. Nous atteignons la base quand nous trouvons des porteurs des employés, la base sommes tous les porteurs moins derniers considérés. Si les porteurs sont dans le n° exorbitant, la base existe mais les comparaisons sont dans le n° exorbitant également elles et la base, infini hypothétique.

 

8) accomplissement de la base :

Une base de V est B constitué à partir des porteurs de n et dans V les porteurs indépendants sont m actuel alors peuvent dire ces porteurs de m de V avec à n - porteurs de m de base de la forme une de B de V.

Faible : le ž la démonstration est selon le principe d'induction, se produit qui est avant pour 1 porteur et alors nous le prolongeons à tous les porteurs :

) nous supposons d'avoir dans V le indépendant soloun de W ₁ linéairement considérant si même. Nous écrivons comme la combinaison linéaire des porteurs de la base, W₁ =  l₁v₁ l₂ v₂ l₃v_{3 ...,} l_nv_{n que} nous notons que cet affinchè W_{2 1} ¹ 0 dans combiencoûte indépendant doit être m tout le l est égal à 0 étant un bas mais si le ¹0 alors également un de W ₁ du l doit être divers de 0 pour pouvoir vérifier l'égalité, nous supposent que ₁ estv et nous selon l'équation v de réécriture₁ dividende pour l₁ selon le membre. À l'équation obtenue donc nous remplaçons à W_{le 1} sa combinaison linéaire et l'obtenons que le ¹ 0 de l'affinchè ₁ est vraiayant l'endroit l, devrons être 0 le coefficient pour lequel il est multiplié, qui est le coefficient de porteursm ₁ W ₁ m₂v₂ m₃ v₃ de W₁doncI _..., m_nv_n ils sont une base de V à combien de B ? Span(W_1, v₂ , v_3, vn).

 

b) le raisonnement analogue est accompli afin de démontrer cela qui vaut la peine également pour les porteurs indépendants de m de V qui ne font pas une partie de la base. La conclusion est que le n° des porteurs de la base et donc la dimension de V ne demeure pas sans changement, est pour celle parle au sujet de l'accomplissement de la base.

 

De cette démonstration nous tirons de nombreuses observations :

A) les bases d'un espace vectorial ont toute la même dimension, pourquoi si on avait de petits porteurs, le gliene pourrait s'ajouter d'un autre, mais étant la base de massimale pour la définition, ci² ce serait une absurdité, la seule situation qui respecte le massimalità de la base est la parité du n° des porteurs entre les bases.

B) Ayant un espace vectorial avec la dimension n, son sottospazi ne peut pas avoir la dimension m > n.

Nous voyons l'heure comme effectuer l'accomplissement à une base :

Nous faisons le cas pour avoir 2 porteurs suivants v₁ = e v₂ =et de vouloir les accomplir à une base de "³ , nous pouvons choisir un des porteurs de la base canonique, mais à ce qu'il nous garantit que les porteurs sont toujours entre de indépendant eux :

Le gauss pour des colonnes, celui est pour des porteurs nous schiarisce un Pò les idées, nous voyons que l'envergure les met en oeuvre de v₁ et v₂ et nous essayent de faire un certain osservazione : l'ébauche d'un système dans la forme à mesurer, donc ces 2 porteurs sont indépendants, sont très clair que le seul porteur de la base qui concourt pour maintenir cette structure de balance sans changement est le porteur et_{les 3} donc comme le segue : et donc ce sont une base d'"³ constitués donc à partir de 3 porteurs indépendants, dont l'envergure est tous les "³ .

9) Spazi vectorial : somme, intersection, complément :

Nous avons analysé qui place des opérations de stiche peut être exécuté ayant le sottospazi 2, le W1 et le W2 de l'espace vectorial V.

W1 ? W2 ? Le ž V l'intersection du sottospazi 2 vectorial est toujours un sottospazio vectorial de V.

Un cas particulier d'intersection est celui-là entre avec et son complément, une telle intersection doit être {0}.

Nous faisons à heure un exemple dessus en tant que calcul de l'intersection entre 2 que vous espacez vectorial, à un tel but est supposés d'avoir l'envergure 2 suivante d'"⁴ V =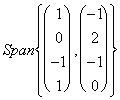 e W =.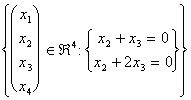

L'intersection qui intéresse à nous, nous pouvons le caractériser installant directement que les porteurs de W, au delà de la réponse aux listes détaillées fournies à partir des 2 équations, également sont contenu dans l'envergure de V.

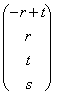
Nous reprenons donc le porteur des coefficients l et m pour V, ébauche du porteur des solutions :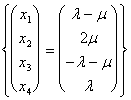

si heure nous remplaçons x₂ et x₃ dans la définition des porteurs de W nous trouvons exactement l'intersection entre le sottospazi 2. de ce que nous gagnons l = m = 0 et pertanto .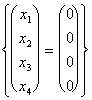

Cela veut indiquer exactement qu'entre le sottospazi deux il y a un certain dim(the V d'intersection donc ? W) = {0}.

W1 ? Le ž W2 n'est pas toujours un sottospazio vectorial de V, ne charge pas au cas de W1 = envergure du porteur de l'appartement et de W2 = d'envergure du porteur, ils représente des marques nous de directement entre orthogonal ils, puis si nous prenons 2 porteurs et de lui nous faisons la somme avec la méthode de parallelogramma, une telle somme s'avérera être un porteur avec la diverse direction concernant tous les autres, donc la somme n'est pas contenue dans V et donc l'union du sottospazi 2 de V est pas nécessairement un sottospazio également il.

W1 W2 ? Le ž V la somme d'une façon généralisée remplace l'union et est toujours un sottospazio vectorial.

Un cas particulier de somme est qu'on a constitué à partir de 2 ensembles desquels on est le complémentaire de l'autre, dans cette condition seulement peut affirmer que la somme est écrite dans une seule manière, une telle somme vient alors défini dirigé.

Dans le cas que l'intersection des 2 place y a divers de { ou } alors il sont plus de manières que pour écrire la somme comme dans le cas suivant : le porteur suivant est eu dans "³, il peut être écrit = =

Nous faisons à heure un exemple dessus en tant que calcul des dimensions de la somme de 2 que vous espacez vectorial, nous plaçons suivons l'envergure d'"⁴ V =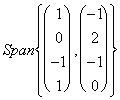 e W =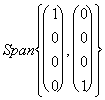uno des méthodes afin de calculer de la somme doit les joindre dans une seule matrice et voir si elles sont les porteurs indépendants, donc comme elle suit :

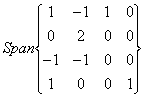Une telle commande dans un tel cas disparaît dirigé vers des colonnes, soit une question elle-même des porteurs et pas des équations.

Toutefois plus exprès au deuxième est également une manière du problème, ce doit mettre en oeuvre la formule de Grassmann, est clairement qu'elles doivent être connues est la dimension de V, de W et également à eux intersezioneed appliqué à suivre :

Le sottospaziU et W vectorial de l'ati 2 de D de V, est valide la relation suivante : Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

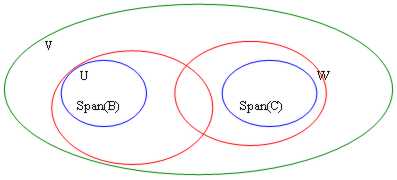
Au bbiamo 2 générateurs, 2 B et C du sottospazi U et W, nous pouvons dire ce B alors ? C est avec des générateurs de U?W. Toutefois nous parlons seulement au sujet de l'envergure et pas au sujet des bases, en fait l'union de 2 bases pourrait également caractériser des porteurs qui ne sont pas indépendants

 

10) avec complémentaire :

Elle est définie avec complémentaire de à, tels l'intégralité de B laquelle n'a pas une certaine intersection avec à et laquelle le tout forme l'espace vectorial B selon la conception successive :

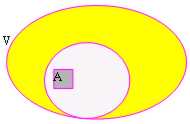
Nous faisons à ce point un exemple dessus quant à la trouvaille un complément déterminé de sottospazio vectorial d'un espace V.

Dans l'exemple sur l'accomplissement de la base, nous avions vu comme accomplir des porteurs de I deux v₁ = e v₂ =à une base d'"³, et le résultat était la sterne du vettori : peut donc dire qu'on ayant le complémentde la dimension 1 de v ₁ est le plan produit des porteurs . Analogue le complément dans "³ du plan produit des porteurs de I v₁ et v₂ est avoir la dimension 1 de porteur.

11) théorème de Grassmann :

Le sottospaziU et W vectorial de l'ati 2 de D de V, est valide la relation suivante : Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

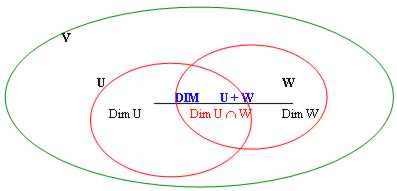
Que le faible de la somme que ce n'est pas tout l'intuisce visuellement étant cru également que dans la somme elles viennent élimine tous les porteurs à vous qui sont d'une manière quelconque superflus dans les dimensions simples du sottospazi. Ceux légèrement est représentés de l'intersection.

Démonstration :

Nous avons _1n UVUV que c'est une base, nous l'accomplissons dans U _{à 1n} UVUV u_{n 1} u_p et dans W ₁aux W UVUV _{de n}W _{n 1}

Nous devons démontrer que les porteurs u qu'ils sont accomplissement de l'uw de porteurs dans U

les porteurs W qu'ils sont accomplissement de l'uw de porteurs dans W

les porteurs u qu'ils sont dans l'intersection de U ? W =

la base de U W doit être un qui est son envergure et entre le indépendant ils

l'affinchè qui est vrai doit être p (n-p) (PS) = n s - p = dim(U W)

ce qui est équivalent à grand : Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

donc B doit être {₁des W UVUV _{de n}u _{n 1}u _pW _{n 1}} et l'affinchè qu'il est indépendant tous les coefficients (qu'eux ne sont pas écrits) doit être = 0. Nous démontrons observer cela " v ? (U?W), " u ? (u) et " W ? (w), mais pour l'essere W v u = 0 ž W = - v - stà donc W de u du ž dedans (U?Le bidon de W)e donc soit écrit comme la combinaison linéaire de v, mais W il est également égal ₁aux W UVUV _{de n}W _{n 1} que donc ils doivent être également indépendant ils afin de vérifier l'égalité, donc W donc tous les coefficients de B sont 0.

 

Beaucoup intéressant pour la mnémonique l'exemple fait à partir de Schoof. V sont supposés un plan et un W un plan orthogonal à lui donc tous les deux avec la dimension 2 :

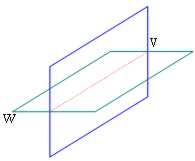
Car il peut noter, l'intersection entre les 2 plans est un droit ayant faible = 1

donc dim(V W) = dim(V) faible (w) - dim(V ? W) = 2 2 - 1 = 3

et en fait 3 est exactement la dimension de l'espace.

 

12) somme directe :

Directement du théorème de Grassmann que le théorème descend la définition de la somme directe dit en fait :

Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

Et de ce bon célèbre qui si l'intersection entre le sottospazi 2 vectorial est nulle, alors la dimension de la somme de l'espace est exactement égal à la somme des dimensions des cumulateurs des espaces :

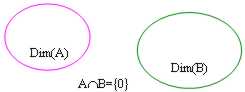
dans les formules Dim(A B) = Dim(A) Dim(B)

et dans ce cas-ci donc la somme est directe défini et été possible pour l'écrire dans une seule manière comme déjà déclarée.

 

13) applications linéaires :

Nous avons analysé le cas dans lequel à un espace vectorial qu'il vient s'est appliqué une fonction et l'image de cette fonction nous l'avons dans un autre espace vectorial.

Nous avons supporté défini une application comme traçant si suivant sont définis :

F(v d'Addizione₁ v2) = f(vdu f(v 1)2)

F(lv)= l f(v)de Moltiplicazione

Par conséquent nous avons fait l'exemple d'une application dans V ? "³ ayant des valeurs dans W ? "² qui est

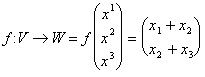nous devons vérifier s'il doit tracer qui est les 2 critères :

a) f(v₁ v2) = f(vdu f(v 1)2)

1° la vallée de membre :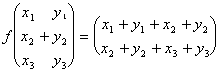

2° la vallée de membre :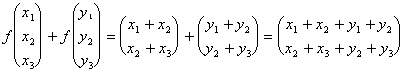

évidemment les deux membres sont donc ébauche égale d'une application linéaire concernant la somme.

b) F(lv)= l f(v)de Moltiplicazione

1° la vallée de membre :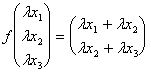

2° la vallée de membre :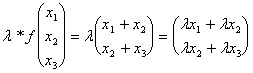

évidemment les deux membres sont donc ébauche égale d'une application linéaire concernant le produit.

 

Un critère court existe alors également afin de déterminer si une application doit tracer qu'elle dérive directement du critère court pour la détermination du sottospazi, celle est :

critère de breve :

 

14) l'image de la fonction s'est appliquée à un espace vectorial :

L'image est définie comme les porteurs W ? W : un porteur v dans V existe : f(v) = W

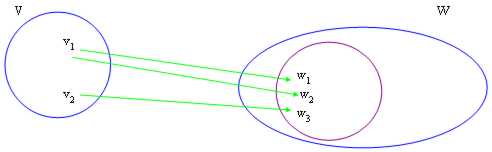
Nous avons alors démontré qu'im(f) est un sottospazio de W et que pour la définition, si l'image de f est tout le W indique alors que f il est suriettiva, des mémoires que tout le cowboy viennent coup au moins d'une flèche.

Pour le calcul des dimensions de l'image elles doivent naturellement être trouvées les solutions de l'impôt de système de la fonction et d'être dans le n° sans limites, pour les exprimer comme une envergure de quelques porteurs. On le suppose comme exemple de devoir trouver les solutions du seguente :

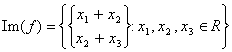
de ce que 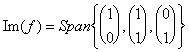c'est équivalent au matrice l'envergure

ce diviene réduit : L'envergure dans laquelle regarde cela un porteur était combinaison pour la délinéation des autres 2, pour lesquels nous pouvons dire qu'im(f) = envergure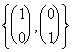 et avons la dimension 2.

 

15) noyau d'une application linéaire :

Au lieu de cela le noyau d'une application ou d'un Ker(f) linéaire est défini tous des porteurs de I v dans V qui finissent dans le 0 de l'image

 

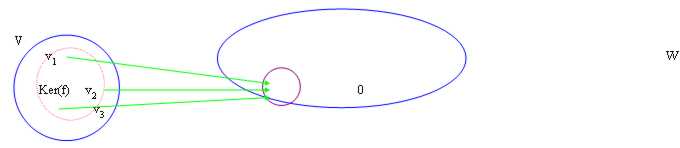
Nous avons alors démontré que Ker(f) est un sottospazio de V.

 

16) une fonction s'est appliquée à un espace vectorial est iniettiva si le ker(f) = {0} qui sont s'il y a des porteurs au noyau :

La démonstration est subdivisée dans 2 parts :

 

) sachant que f il est iniettiva, nous essayons d'affirmer ce Ker(f) = {0}ossia que le noyau est vide.

Nous prenons à un porteur v ? Ker(f) et nous indiquent que ce doit être f(v) = 0 étant la fonction d'iniettiva, nous pouvons mais affirmer cela f(0) = 0 et donc v = 0 qui est le porteur n'existent pas.

 

b) Savoir que le noyau est vide je dois démontrer que f il est l'iniettiva qui est que chaque flèche simple de cowboy est frappée d'une.

Je prends 2 flèches, x et y et démontre qu'ils ont frappé le f(x) différent et le f(y) de 2 cowboys, s'ils frappent le mêmes un f(x) = f(y) de cowboy étaient alors la même flèche X = y. est démontrés tirant profit des linéarités de l'énonciation de f que ce doit être f(x) - f(y) = 0 dans combien nous supposons le f(x) = le f(y) et nous voulons réussir dedans pour dire le ce x = y.

Appliquant les linéarités nous déduisons que 0 = f(x - y) mais le noyau doit être donc x vide - y = 0 qui est x = y.

Nous voyons à ce point car le noyau est ker(f) estimé, s'avère assez d'intuitivo pour penser que nous devons trouver toutes les solutions de la fonction qui valent la peine 0, donc nous nous ramenons à l'étude d'un système homogène.

On le suppose de devoir calculer les dimensions du noyau suivant de l'application f : "³ dans "².

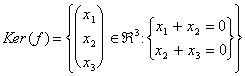équivalent au matrice

L'ébauche d'un système qui normalement doit être résolu par le gauss pour des colonnes mais est dans ce cas-ci déjà dans la forme à mesurer et a 2 équations pour 3 incognito, donc une est incognito librement et déjà intuiamo que la dimension sera 1.

En particulier : = ce dernier porteur peut également écrire r * de ce qu'implicitement il suit cela : Ker (f) = Envergure.

 

17) représentant Matrix d'une application linéaire :

La matrice représentative accomplit une opération qui divers semblerait quelque peu complexe, il reçoit comme revenu une base contenante de l'espace vectorial le dominion, une base contenante du codominio vectorial de l'espace et la fonction qui allient le dominion et le codominio, et fournit comme l'évasion une manière exprès afin de calculer la valeur de l'image pour un n'importe quel porteur du dominion.

Normalement car les bases choisissent canoniques, toutefois personne n'interdit pour employer les bases n'importe quel purchè a fini donc comme espaces d'elles se produisent à vous.

L'explication de car elles sont gagnées et les limites de dialtri viendront dynamiquement fourni ; nous voyons en tant que tels que la matrice suivante pour l'application est gagnée pour tracer :

g : "³ ® "² : g == nous devons en premier lieu la commande que cette application doit tracer qui est que les 2 égalités suivantes sont respectées :

1) g(v₁ v2) = g(vdu g(v 1)2)

2) g(lv) = lg(v)

Nous choisissons la base de l'heure une pour "³, naturellement ces canonique et₁ = , et₂ = , et₃ = .

Analogue nous choisissons la base de l'heure une pour "², immobile qui un canonica f₁ = , f₂ =.

À ce point nous avons tous et nous pouvons donc passer pour décrire la construction de la matrice représentative de g concernant les 2 bases utilisées.

Les colonnes de la matrice représentative en fait sont constituées à partir de l'application de la fonction g aux porteurs constitutifs la base, c'est et₁ , et₂ , et₃ . Dans notre exemple, g(e1) =, g(e2) = , g(e3) =

et la matrice représentative est donc : .

là où le n° des colonnes il est égal à la dimension du dominion et au n° des lignes il est égal à la dimension du codominio.

À ce point sommes nous en position à calculer ce qu'arrive facilement simplement au porteurv ₁ = quand à lui nous nous appliquons la fonction g, effectuant le produit entre la matrice de rappesentativa et ce porteur :

*= où 5 sont obtenus multipliant 1ª la ligne pour 1ª la colonne tandis que 7 la multiplication normale d'un porteur pour un est obtenus multipliant 2ª la ligne pour 1ª la matrice de colonne deuxièmes.

Naturellement le même résultat pourrait être obtenu remplaçant le porteur v ₁dans la description de la fonction directement, toutefois pour de grands calculs que le procédé meilleur est ceci a à peine illustré.

Vous vous notez que le porteur obtenu va donc signifié comme un porteur de coordonné concernant la base f fourni pour le codominio.

C'est l'intuitivo à gagner que connaissant seulement la matrice représentative la fonction peut être gagné simplement multipliant une telle matrice pour le porteur générique du dominio : *= .

Le grade d'une matrice est défini la dimension de son image, dans ce cas-ci le grade de la matrice représentative est trouvé, conclusion de l'image qui est avec des solutions qui car nous avons vu qu'exprès en termes d'envergure et porteurs qui font une partie de l'envergure doit être tout l'indépendante, toutefois une fonction ne peuvent pas être parlées au sujet d'une base dans de combien coûte une restriction avec et donc l'envergure ne peut pas être tout avec donc comme à la place devrait être pour une base.

 

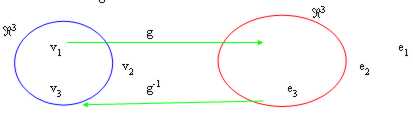
18) matrices de représentant des fonctions composées :

Le concept de la fonction composée est très célèbre et est riepilogato dans la figure :

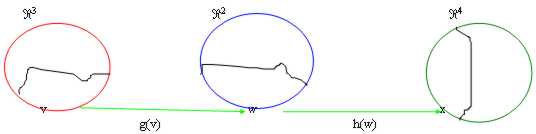
On le suppose :

g : "³ ® "² : g == dont la matrice représentative est : .

h : "² ® "⁴ : h =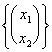= 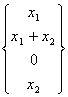dont la matrice représentative est : .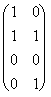

La matrice représentative du ° composé g de la fonction h est le produit des 2 matrices représentatives :

° de h g = *=

Au résultat analogue mais dans un amniera plus laborieux il a été atteint remplaçant la fonction les deux éléments génériques de la fonction

g = dans la fonction h = atteignant le ° de h g =

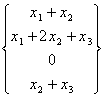
cela a appliqué aux porteurs de la base de "⁴ et₁ = , et₂ = , et₃ = , et₄ =

il fournit le même ossia précédent de résultat : exactement ° de h g = .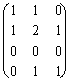

En composant une matrice doit être attention à comporter en particulier si elle est une opération ou moins de sensata, nécessité

pour être avec du passage de la même dimension dans l'arrivée concernant la dimension dans le départ, pratique :

la composition "² est " ® ⁴"® ³possibles

mais la composition "² n'est pas possible ® ("⁴ "1)® "³

En fait une écriture du type ( "⁴ "1) n'ont pas le sens.

 

19) applications linéaires biiettive :

Une fonction car nous savons est biiettiva quand est est iniettiva (chaque élément de l'image peut être fonction d'un seul élément du dominion) ce suriettiva (l'image est tout le codominio).

les intérêts de biiettività à nous fundamentalally pourquoi il il affinchè de condition une matrice représentative de la fonction g est inversible que soit existe l'un g inverse^-1.

La première prérogative d'une matrice inversible est que c'est à angle droit qui est que le n° des lignes est égal au n° des colonnes.

Le procédé afin de la calculer est suivant :

de l'illustration on le comporte bien que notre portée est de caractériser ces éléments v dont l'image est _{le I} et le codominio bas c'est-à-dire, qui est obtenu résolvant le g(v linéaire i)= et _Ide système.

On suppose que la matrice représentative est :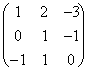alors le système linéaire est :

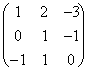* = et₁ = ž = ce c'est 1ª la colonne de la matrice inverse.

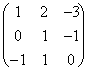* = et₂ = ž = ce c'est 2ª la colonne de la matrice inverse.

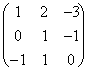* = et₃ = ž = ce c'est 3ª la colonne de la matrice inverse.

donc la matrice inverse de la matrice représentative 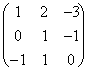est la matrice .

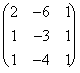Vous vous notez que la matrice suivante pourrait être atteinte le même résultat résolvant :

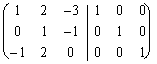afin d'obtenir vers la droite la matrice inverse que je dois essayer pour ramener la matrice de la gauche à une matrice diagonale donc comme au moment où elle est vers la droite.

Nous commençons à réduire à un système à la balance : 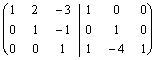et alors laissant du pivot bas, nous créons les 0 excédents tout le pivot avec la méthode habituelle de gauss, nous obtenons : 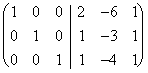cela, vers la droite il présente la matrice inverse exactement que nous avons essayée et est égal à celle-là trouvée avec la longue méthode.

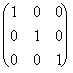
Je peux d'ailleurs commander que le résultat obtenu est corrigé, en fait si je multiplie la matrice représentative pour la matrice inverse correspondante que je dois trouver encore la base dont ils sont partis pour la définition du rappresentativa de matrice. Par conséquent dans le precedente de cas : *=

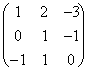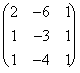Là où le produit est exécuté aux usuals :

ligne 1ª pour la colonne 1ª

ligne 2ª pour la colonne 1ª

ligne 3ª pour la colonne 1ª

ligne 1ª pour la colonne 2ª

etc......

ligne 3ª pour la colonne 3ª.

 

20) quand une matrice représentative n'est pas inversible :

Nous ne saurons pas jamais a priori si une matrice est inversible ou moins, la seule manière afin de rendre du compte que nous doit pour porter le péché de calculs en avant quand il n'est pas atteint à une absurdité comme suivre : 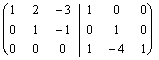là où 3ª l'équation nous indique que 0 sont égal à 3 divers coefficients, cela il est 3 temps absurdes dans combien 0 coûte égal seulement à 0.

Un autre cas de l'absurdité des équations est suivant : 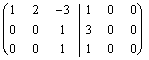là où le 3ª incognito il nous indique que x₃ doit être égal à 1 tandis qu'2ª l'équation nous indique que x₃ doit être égal à 3, ils ne peuvent pas contemporaeamente être vrais tous les deux, donc le système n'a pas la solution et que la matrice représentative n'est pas donc inversible.

 

21) changement de base :

L'heure est censée avoir une matrice représentative d'"³ a installé la base canonique en second lieu, et de vouloir à la place l'installer base en second lieu suivante : l'et₁¹ = , et₂¹ = , et₃¹ = .

La matrice représentative concernant la base canonique est seguente : 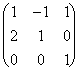l'heure de nécessité pour calculer la matrice représentative concernant la nouvelle base, montant observant que les colonnes sont exactement la fonction a appliqué aux porteurs de singloli de la base. Nous procédons donc :

f(e₁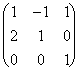1) = *=, f(e₂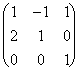1) = *= , f(e₃1) = *=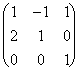

Maintenant je dois trouver quels coefficients, vous multiplie pour la base et¹ donne comme le résultat ces derniers me 3 porteurs, donc :

f(e₁1) = ayant comme le soluzioni :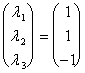

que c'est 1ª la colonne de la matrice représentative B concernant la base et^{le 1} analogues :

f(e₂1) = ayant comme le soluzioni :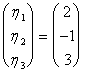

f(e₃1) = ayant comme le soluzioni :

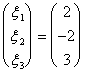
Par conséquent la matrice représentative concernant la nouvelle base est.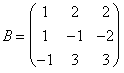à qui colonnes sont le f(e de porteurs₁1), le f(e₂1), le f(e₃1).