Ortonormali Autovalori et bases
Autovalori
1) définition d'autovalore :
Il y a des applications pour lesquelles à un porteur sûr v, par l'application un son multiple correspond, en f(v) de formules = lv dans un tel cas que la valeur de v multiple est l'autovalore tandis que le porteur correspondant v est l'autovettore. À un même autovalore plus d'autovettori peut correspondre, dans un tel cas à de la prise d'autovettori le nom de l'autospazio.
2) quand la base de l'autovettori pour un existe une application :
Pour une application une base d'autovettori existe quand ce peut être respect représenté à une base particulière d'une matrice diagonale.
3) quand une application est diagonalizzabile :
Une application est diagonalizzabile quand elle a tout l'autovalori sur le champ et leur variété d'algebrica coïncide avec la variété géométrique correspondante de cette dérive que la somme de la nécessité géométrique de variétés est égale aux dimensions du centre serveur de l'espace.
4) ce qu'elles servent à l'autovalori dans le calcul de f n = f * f * f.... * à f :
Ils servent au diagonalizzare la matrice représentative de l'application f, à un tel point la puissance est facilement exécuté ennesima directement sur la matrice diagonale et finalement le changement de la base de est fait en utilisant les mêmes formules.
5) comme l'arrangement à l'oeil de la matrice l'autovalori d'une application :
Simplement elles sont les valeurs qui abaissent le grade d'une matrice, que la rendent qui n'est pas maximum.
6) que le type d'autovalori a une projection :
Une projection est une application qui si elle vient effectué 2 fois donne le même résultat qui est obtenu l'effectuant une fois simple, dans les formules : f(v) = lf(f(v) de v) = l(lv) = l2v
Basé sur combien ledit lv = l2v et donc l(l-1) = les 0 donc autovalori coûtent 0 et 1.
7) quand une matrice à et une matrice de B peuvent être conjuguées :
Quand une telle matrice C existe ce B = C * au *cle -1 qu'elle se produit seulement à condition qu'à et B a le même autovalori avec les mêmes variétés géométriques et les mêmes variétés d'algebriche.
8) Critère afin de caractériser immédiatement une partie de polynôme caractéristique d'une la matrice :
Le coefficient d'Il de la limite du degré n est (-1)n tandis que le coefficient de la limite du degré n-1 est (-1)n * tracez à, finalement le coefficient de la limite du degré 0 à la laquelle est la limite célèbre est égale à de détermination de la matrice.
9) quand une matrice est le nilpotente et ce type d'autovalori a :
une matrice est nilpotente quand un sa puissance de degré n > = la 1 matrice nulle de é.
l'autovalori sont nécessairement chacun des 0.
Formes quadratiques
10) comme signature d'équation quadratique une forme est trouvée :
La devise est estimée un certain dopodichè caractéristique polynôme si le signe de l'autovalori avec la méthode de Cartesio.
11) Enounce la règle de Cartesio pour l'endroit de la signature des solutions d'un polynôme :
le polynôme est commandé du degré maximum avec le degré minimal, avec une telle devise de point :
racines positives de n° = n° des variations du signe dans le polynôme
le n° enracine le nulle = le degré minimal actuel dans le polynôme
racines négatives de n° = le degré maximum de polynôme - (le positif de n° enracine les racines nulles de n°)
Produits de Scalari
12) quand une forme est bilinéaire :
Une forme est bilinéaire quand elle doit tracer le respect aux deux variable, nécessité qui est soit vérifiée cela
a) f(lv mv1,w) = lf(v, w) f(v 1,wde m)
b) f(v,lW mW1) = lf(v, w) f(v de m, W1)
13) ce qui est un produit à s'élever et le quel matrice associée est à elle :
Un produit à s'élever est une telle forme bilinéaire symétrique qui est ce f(v, w) = f(w, v).
La matrice associée à elle est une symétrique, une telle matrice qui est que l'élémentà l'ij =au ji .
14) définition du produit pour monter canonique :
Un produit pour monter canonique est positif une forme bilinéaire symétrique définie, vaut la peine de dire que < v,v > il est > = 0 et < v,v > que 0 matrices associées par La à lui sont = 0 > v = est une matrice symétrique de détermination avec le positif.
< v,w > = v1 *W1 v2* W2 ...... vn * Wn
15) typologie des produits de scalari :
Est défini le positi de produits de scalari à vous, semidefined existent positi, défini nié à vous, semidefined nié à vous à vous, indéfini, semidefined le positi de produits de scalari à vous et nié il y a nécessairement dégénéré qu'assument non seulement la valeur 0 pour le porteur 0 .
16) comme distance entre un point et un sottospazio est trouvé :
On l'avère gagner la projection orthogonale du point sur le sottospazio et calculer la distance concernant ce point caractérisé. La projection orthogonale peut être gagnée facilement qui intyersezione entre le sottospazio et le droit passant pour le point p et ayant que directeur de porteur le porteur orthogonal au plan qui si le plan a la hache d'équation par le cz = le d est alors le porteur (à, b, c).
Autrement la distance par la formule mettent en boîte
plus rapidement soit calculée 
Elle est de noter cela dans "n qu' il vaut la peine une prolongation logique de cette formule gagnant l'heure pour le temps.
17) < < x, v>v, v>v sont égal à < x,v > < v, v>v :
, le passage est personne autorisée, en fait < x,v > il doit s'élever et un porteur et ne peut pas donc être porté extérieurement au produit pour monter mêmes.
18) quand une forme est au sesquilineare :
Une forme est au sesquilineare quand la propriété deux suivante sont vérifiées :
f(lv mv1,w) = lf(v, w) f(v1,wde m)
f(v, lW mW1) = lf(v, w) f(vde m, W1)
19) ce qui est un produit de hermitiano et le quel matrice associée est à elle :
Un produit de hermitiano est une forme au sesquilineare qu'il apprécie le hermitianità, vaut la peine à la parole de la propriété suivante :
La matrice associée à elle est une matrice symétrique dans laquelle l'élémentà l'ij qu' elle est conjuguée de l'élémentau ji doit d'ailleurs être B = Bt
20) définition de produit canonique de hermitiano :
Un produit canonique de hermitiano est une forme au positif défini par hermitiana de sesquilineare, vaut la peine de dire que < v,v > il est > = 0 et < v,v > que 0 matrices associées par La à lui sont = 0 > v = est une matrice symétrique de détermination avec le positif.
< v,w > = v1 *W1 v2*W2 ...... vn * Wn
21) comme déterminer si une matrice est hermitiana :
Dever à être B = Bt qu'il implique que sur les vrais éléments de diagonale seulement dans combien doit être présent le congé de transposition la diagonale et = sans changement > ? ".
22) caractéristique de la matrice associée à un produit pour mesurer ou au positif défini de Hermitiano :
Ils sont les deux matrices ayant déterminer le positif.
23) écrivent transposé conjugué de 
et dire si c'est hermitiana :
Ici il y a le trabocchetto, en fait conjugué d'un n° voit
au changement du signe la partie imaginaire et la vraie partie donc
transposée conjuguée n'est pas : 
clairement
transposé conjugué n'est pas hermitiana dans combien coûte divers
lui donne la matrice de départ.
Bases D'Ortonormali
24) il a le sens de parler au sujet des bases d'ortonormali en dehors pour avoir présenté le concept de produit pour s'élever :
Dans combien elles ne doivent pas être constituées à partir des porteurs qui sont orthogonaux entre d'eux et c'est mesurable par un produit pour s'élever seulement qu'il concourt la mesure des angles et de la distance.
25) que la base d'ortonormale de l'autovettori est l'avantage principal d'une :
Foi que le plus grand avantage est que la matrice inverse est banally égale à la matrice transposée.
D'ailleurs une base d'ortonormale est la seule par laquelle il est possible de réaliser que l'isometrie qui est des transformations qui ne changent pas des angles ni l'une ni l'autre dimensions de l'objet de départ et donc ils ne le déforment pas.
26) décrivent les étapes d'Ortonormalizzazione di Gram - Schmidt :
) c'est v1 le normalisé v1 *
b) un devient selon le porteur de la base d'ortonormale à l'un premier v2 '= v2 - < v2, v1 * > v1 *
c) est v2 normalisé l'' v2 *
d) le troisième porteur orthogonal formé au sottospazio devient de v1 * et v2 * qui est :
v3'= v3 - < v3, v1 * > v1 * - < v3, v2 * > v2 *
et) c'est v3 normalisé le ' v3 *
27) que le sens doit base de l'ortonormalizzare un :
Une application a seulement l'autovettori orthogonal si elle qui est a tout l'autovalori distingué si à chaque autovalore correspond un autovettore simple, autrement l'autovettori inhérent au même un autospazio ne peut pas également être orthogonal, dans un tel cas il a le sens de procéder à Ortonormalizzazione di Gram-Schmidt-Schmidt que commencer d'un de l'autovettori 3 crée une base d'ortonormale qui réussit au diagonalizzare avec une transformation orthogonale la matrice représentative dont nous avons trouvé l'autovalori et l'autospazi.
28) Normalizzare le porteur 
:
Le tour doit estimer la norme de tout le porteur, alors pour diviser 1/3 pour une telle norme et pour se multiplier pour le porteur.
29) comme calculer la projection d'un point sur les porteurs d'un ortonormale bas :
Les coordonnées rapportées à un axe de la base ne sont
pas autre que le produit à la balance du porteur v pour le débiteur
de la base divisée la norme du débiteur qui a clairement 1 ans donc
la valeur de la coordonnée d'un respect de porteur à un débiteur
d'une base d'ortonormale n'est pas que le produit à l'élever du
porteur v pour le débiteur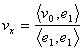 
.
30) décrivent la méthode des moindres carrés pour l'identification de la droite d'une meilleure approximation qu'une série de données les éprouve :
La méthode donnée quelques points concourt pour caractériser le droit que meilleur les rapproche, à un tel but écrit le système linéaire non compatible contenant toutes les équations génériques de vous passer directement pour les points ºde l x de m y dans une telle manière crée une matrice d'A(x) = portée de b notre est de projeter le porteur b sur le sottospazio des solutions du système d'A(x) qui est sur Im(A(x)). Ceci dans pratique est obtenu qui installe l'égalité t* = t* b.
À ce point le système obtenu est une matrice 2*2 de B à 1° le membre et un porteur c 1*2 à selon le membre, est résolu avec la méthode de Cramer, qu'il trouve le coefficient de x qui le rapport entre de détermination de la matrice obtenue remplaçant à B au lieu de 1ª le porteur c de colonne et de détermination de B. Le coefficient du y trouve quel rapport entre de détermination de la matrice obtenue remplaçant à B au lieu de 2ª le porteur c de colonne et de détermination de B.
Applications Orthogonales
31) définissent une application orthogonale et pour décrire des caractéristiques :
la relation < T(v), T(w) > = < v, W > vaut la peine sur le champ de le vrai.
signifié est donc qu'il ne vient pas métrique changé de l'espace l'image, vaut la peine de dire qu'un objet auquel nous nous appliquons une transformation unitaire ne vient pas déformé.
32) comme déterminer si une matrice est orthogonale :
La colonne de porteurs de à la base d'ortonormale de la forme une.
a) doit être |det B| = 1
b) s'il est vrai a) est commandé que la colonne de porteurs aient la norme 1
c) s'il est vrai b) est commandé que la colonne de porteurs soient mutuellement orthogonale
d) sur option à la commande ce Bt * B = identification
33) si j'ai trouvé pour un autovalori y 1 de l'application2 et y2 avec l'autovalori Vy1 et le Vy2 normalisent à vous, car je diagonalizzare de bidon l'application et en tant qu'elle est fait au diagonalizzata de matrice :
Je peux réunir l'autovettori dans une matrice orthogonale du changement de la base par lequel la matrice représentative est réduite à une matrice diagonale sur laquelle la diagonale pour la note apparaît l'autovalori.
34) la matrice orthogonale pour le diagonalizzare un est une matrice représentative nécessaire :
Pas, une matrice représentative vient diagonalizzata également d'une base d'autovettori non normalisée, le problème est celui d'une telle manière par porteur auquel nous appliquons le matrappr est divers du porteur obtenu faisant le changement de la base vers la forme de diagonalizzata, appliquant le diagonalizzata de matrappr et alors nous le rapportons dans la vieille base.
Applications Unitaires
35) définissent une application unitaire et pour décrire des caractéristiques :
La relation < T(v), T(w) > = < v, W > vaut la peine sur le champ des complexes.
Signifié est donc qu'il ne vient pas métrique changé de l'espace l'image, vaut la peine de dire qu'un objet auquel nous nous appliquons une transformation unitaire ne vient pas déformé.
36) comme déterminer si une matrice est unitaire :
a) doit être |det B| = 1
b) s'il est vrai a) est commandé que la colonne de porteurs aient la norme 1
c) s'il est vrai b) est commandé que la colonne de porteurs soient mutuellement orthogonale
d) sur option à la commande ce Bt * B = identification
37) si la colonne de porteurs d'une matrice à sont une base orthogonale, à elle est unitaire :
Pas, ils doivent être une base d'ortonormale.
38) quand la matrice est vraie pour une cette B = Bt = B-1 :
Quand la matrice est est Hermitiana unitaire cela.
39) que l'artifice peut être employé afin de trouver les racines d'une caractéristique polynôme du degré 2° sur les complexes :
La limite célèbre est le produit des solutions pour lesquelles si comme exemple une solution est et également la limite célèbre est alors l'autre solution est évidemment également lui I.
40) si au cours de la recherche des racines d'une
caractéristique polynôme du degré 2° sur les complexes elle est
rencontrée 
pendant qu'elle est décomposée :
est considéré = et c'est -2i portant alors résolu la
forme polaire et en appliquant la formule de De Moivre pour les
puissances des nombres complexes. Porter commençant dans la
forme polaire -2i.
| -2i | = 
tandis qu'arg(-2i) =
donc dans la forme polaire nous ont le 
donc = 
.
Applications Symétriques
41) définissent une application symétrique et pour décrire des caractéristiques :
Une application est symétrique quand la vérification qui le < f(v), W > = < v, f(w) >.
42) en tant que lui est fait à la matrice d'une application symétrique :
C'est une matrice pour laquelle l'élémentà l'ij est égal à l'élémentau ji.
43) dont la détermination de nous s'occupe d'une symétrie :
Det = -1 en fait les transformations d'isometriche sont tout et exposent au soleil les rotations et le simmetrie et savent que le simmetrie ont déterminer -1.
44) dont la détermination de nous s'occupe d'une rotation :
Det = les transformations de 1 en fait isometriche sont tout et exposent au soleil les rotations et le simmetrie et savent que les rotations ont déterminer 1.
45) quand une application est antisymmétrique :
Une application est antisymmétrique quand la vérification qui le < f(v), W > = -<v, f(w) >.
46) en tant que lui est fait à la matrice d'une application antisymmétrique :
C'est une matrice pour laquelle l'élémentà l'ij est a égal -au ji , de ceci il suit que ce sur le 0 diagonal sont présent choisissent, dans combien doit être t= - A.
47) décrivent les matrices d'anti-Hermitiane :
C'est une matrice pour à la laquelle l'élémentà l'ij est a égal -au ji , de ceci il suit cela sur la diagonale qu'elles sont les solos actuels vous finissez avec la vraie partie nulle, dans combien doit être t= - .
Détermination
48) si Det = à 7, combien vaut la peine Det (B-1 à B) :
Il vaut la peine 7 pourquoi de détermination est une fonction invariable pour le changement de la base.
49) Enounce le théorème de Binet sur ceux de déterminations :
Det (Ab) = Det(A) * Det(B).